ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В вертикальном направлении (действует сила тяжести, направленная вниз):
1. Положение и скорость тела в момент t1 = 1 с
2. Максимальная высота и дальность полета
Максимальная высота подъема соответствуем моменту времени, когда
Так как тело не вылетело из ямы, определяем дальность полета относительно дна ямы:
Условие падения на дно ямы:
Перемещение равно:
Скорость равна
Ускорение равно:
Графические зависимости
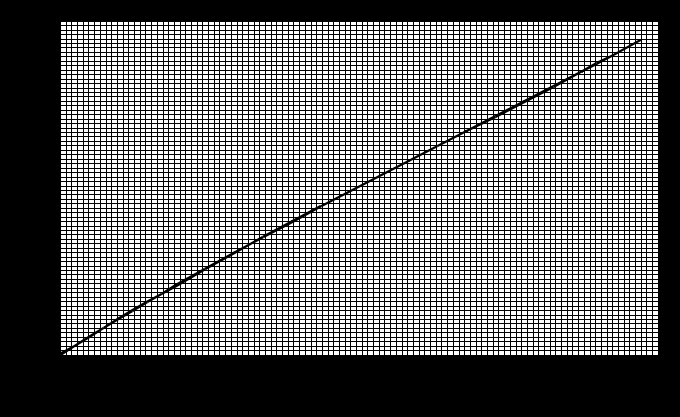

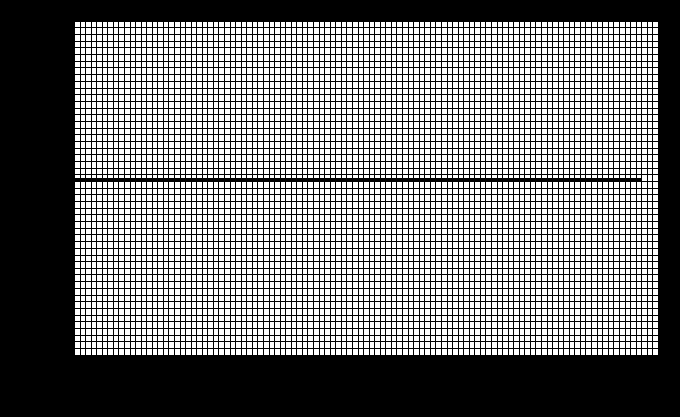
Задача № 4
4.1. С наклонной плоскости высотой
h и длиной склона 10 м скользит тело массой m. Коэффициент трения на всём пути равен k. Найдите:
а) скорость движения υ тела у основания склона, путь, пройденный телом по горизонтальной части пути до остановки;
б) кинетическую энергию Wкин у основания склона, долю полной энергии, затраченную на нагрев наклонной плоскости, работу силы тяжести;
в) постройте графическую зависимость Wкин = f(х) на всём пути.
Исходные данные
| Вариант | Задача | m, кг | h, м | k |
| 7 | 4.1 | 4 | 1 | 0,07 |
Решение
На высоте h тело обладает потенциальной энергией:
Часть этой энергии переходит в кинетическую, а другая часть затрачивается на нагрев поверхности (работа сил трения).
На наклонной плоскости сила трения равна:
Работа силы трения (нагрев поверхности):
Кинетическая энергия у основания склона:
Скорость у основания склона:
Кинетическая энергия затрачивается за работу против сил трения на горизонтальном участке:
– сила трения равна:
– работа силы трения:
Отсюда пройденный путь до остановки:
Графическая зависимость Wкин = f
(X) на всём пути
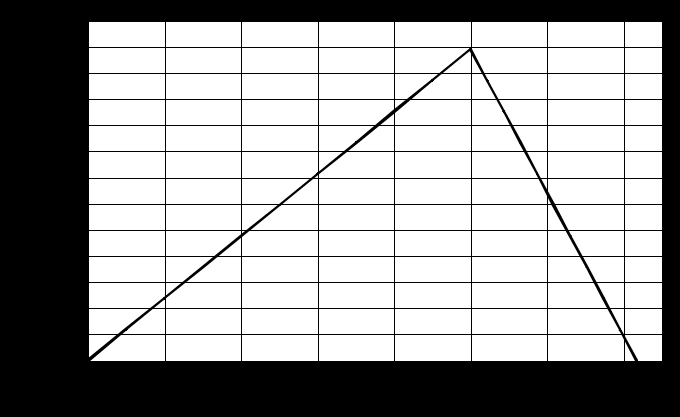
Задача № 5
5.5. Человек стоит на диске, который сначала неподвижен, но может вращаться относительно вертикальной оси, проходящей через его центр. Момент инерции диска с человеком J. В руках человек держит колесо, ось которого вертикальна и расположена на расстоянии ℓ от центра диска. Колесо вращается с угловой скоростью ω. Определить частоту, с которой будет вращаться диск после того, как человек повернет ось колеса на 180. Масса маленького колеса m1, радиус R.
Исходные данные
| Вариант | Задача | m1, кг | ω, рад/с | ℓ, м | J, кг∙м2 | R, м |
| 7 | 5.5 | 2 | 2 | 0,8 | 48 | 0,2 |
Решение
Считаем, что колесо представляет собой кольцо.
Момент инерции кольца относительно собственной оси:
Момент инерции кольца относительно оси диска:
Момент импульса кольца и всей системы «кольцо – человек – диск» (так как все остальное – неподвижно):
После переворачивания колеса момент импульса системы:
По закону сохранения момента импульса:
Отсюда
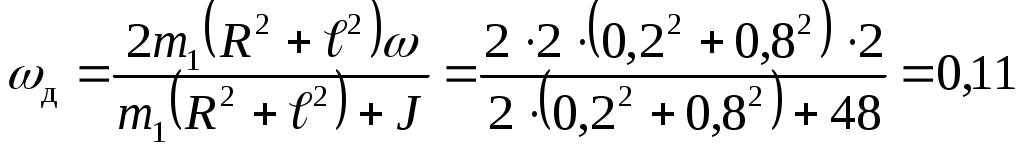 рад/с
рад/с