Файл: Обработка сигналов введение в теорию сигналов введение в теорию сигналов общие сведения и понятия Понятие сигнала.doc
Добавлен: 10.01.2024
Просмотров: 84
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ОБРАБОТКА СИГНАЛОВ 1. ВВЕДЕНИЕ В ТЕОРИЮ СИГНАЛОВ
1. ВВЕДЕНИЕ В ТЕОРИЮ СИГНАЛОВ
1.1. Общие сведения и понятия
Понятие сигнала. В технических отраслях знаний термин «сигнал» (от латинского signum – знак) очень часто используется в широком смысловом диапазоне, без соблюдения строгой терминологии. Под ним понимают и техническое средство для передачи, обработки и использования информации, а по существу, материальный носитель определенного информационного сообщения; и физический процесс, представляющий собой материальное воплощение информационного сообщения - изменение какого-либо параметра носителя информации во времени, в пространстве или в зависимости от изменения значений каких-либо других аргументов; и форму представления данных в виде последовательности значений определенной скалярной величины, как правило – амплитуды, измеренной во времени; и смысловое содержание определенного физического состояния или процесса, как, например, сигналы светофора, звуковые предупреждающие сигналы и т.п.
Применительно к процессам регистрации и обработки результатов наблюдений, которые имеют место во всех областях науки и техники, понятие «сигнал» очень часто отождествляют с понятиями «данные» и «информация». Действительно, эти понятия взаимосвязаны и не существуют одно без другого, но относятся к разным категориям.
Информация (от латинского informatio - разъяснение, осведомление, изложение), наряду с материей и энергией, принадлежит к фундаментальным философским категориям естествознания. По определению Норберта Винера, основоположника кибернетики, «информация есть информация, а не материя или энергия».
Информация обладает определенными свойствами.
Первое свойство — способность управлять построением всех физических структур, начиная от электрона и заканчивая живыми организмами. Базируется это свойство на положении о том, что каждая элементарная частица (электрон) несет информацию о самой себе.
Второе свойство — способность сохраняться в течение любых промежутков времени. К примеру, молекула РНК хранит в себе некий чертеж, который может представлять собой чертеж простейшего организма (вируса) или чертеж столь сложной системы
, как человеческий организм. Несмотря на сложность, она весьма стабильна и в широком диапазоне изменения внешних условий сохраняется сколь угодно долго!
Третье свойство (противоположное второму) — способность изменяться во времени. Возможно как разрушение, так и совершенствование информации.
Четвертое свойство — способность переходить из пассивной формы (информация просто хранится и никак не проявляется) в активную (информация непосредственно участвует в процессе построения некоторой структуры). Обратное этому свойству — процесс запоминания или записи информации (то есть перехода ее из активной в пассивную форму).
Пятое свойство — способность быть переданной на расстояние. Это свойство непосредственно следует из свойства информации к сохранению.
Шестое свойство — способность подвергаться переработке. Например, в живой природе молекула РНК управляет синтезом конкретного белка, выбранного из бесчисленного множества, всегда без сбоев и ошибок.
Седьмое свойство — способность подвергаться измерению. Если информация — физическая величина, то ее можно измерить.
Впервые такую меру предложил в 1928 г. американский ученый Р.Хартли. Измерить количество информации, по Хартли, — значит пересчитать количество возможностей, одна из которых реализуется в данный момент, а затем взять логарифм от этого количества.
Что касается данных (от латинского datum – факт), то это совокупность фактов (результатов наблюдений, измерений) о каких-либо объектах, явлениях или процессах материального мира, представленных в определенном (количественном или качественном) и, как правило, формализованном виде. Это не информация, а только атрибут информации - сырье для получения информации путем соответствующей обработки и интерпретации.
Принимая во внимание изложенное, под термином «сигнал» в строгом смысле этого слова в данном курсе будем понимать определенным образом организованное отображение определенных данных о характере изменения в пространстве, во времени или по любой другой переменной физических величин (рис. 1.1.1), физических свойств или физического состояния объекта исследований. А так как данные содержат определенную информацию, как об основных целевых параметрах объекта исследований, так и о различных сопутствующих и мешающих факторах измерений, то в широком смысле этого слова можно считать, что сигнал является отображением общей измерительной информации. При этом материальная форма носителей сигналов, равно как и форма их отображения, значения не имеет.
Сигнал - это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а цель обработки сигналов - извлечение сведений, которые отображены в этих сигналах и преобразование этой информации в форму, удобную для восприятия и использования.
С понятием сигнала неразрывно связан термин регистрации сигналов, использование которого также широко и неоднозначно, как и самого термина сигнал. В наиболее общем смысле под этим термином можно понимать операцию выделения информационного сигнала и его преобразования в форму, удобную для дальнейшего использования, обработки и восприятия. Так, при получении информации о физических свойствах каких-либо объектов под регистрацией сигнала понимают процесс измерения физических свойств объекта и перенос результатов измерения на материальный носитель сигнала или непосредственное энергетическое преобразование каких-либо материальных параметров объекта в информационные параметры материального носителя сигнала (как правило, электрического). Но так же широко термин регистрации сигналов используют и для процессов выделения уже сформированных сигналов, несущих определенную информацию, из других сигналов (радиосвязь, телеметрия и пр.), и для процессов фиксирования сигналов на носителях долговременной памяти, и для многих других процессов, связанных с обработкой сигналов.
Шумы и помехи. При регистрации сигналов, несущих целевую информацию, в сумме с основным сигналом одновременно регистрируются и мешающие сигналы - шумы и помехи самой различной природы (рис. 1.1.2). К помехам относят также искажения полезных сигналов при влиянии различных дестабилизирующих факторов на процессы измерений. Выделение полезных составляющих из суммы зарегистрированных сигналов или максимальное подавление шумов и помех в общем информационном сигнале при сохранении его полезных составляющих является одной из основных задач первичной обработки сигналов.
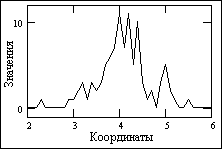
Рис. 1.1.1. Сигнал. Рис. 1.1.2. Сигнал с помехами.
Следует заметить, что деление сигналов на полезные и мешающие является достаточно условным. Источниками мешающих сигналов также являются определенные физические процессы, явления или объекты. При выяснении природы мешающих сигналов они могут переводиться в разряд информационных.
Размерность сигналов. Простейшими сигналами являются одномерные сигналы, как, например, звуковые сигналы, сейсмические импульсы s(t) и т. п. Значения одномерных сигналов зависят только от одной независимой переменной, как, например, на рис. 1.1.1 и 1.1.2.
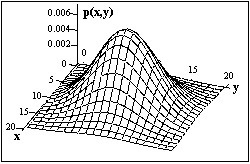
Рис. 1.1.3. Двумерный сигнал.
В общем случае сигналы являются многомерными функциями пространственных, временных и прочих координат – интенсивность компьютерного изображения р(x,y) (рис. 1.1.3), сейсмическая волна вдоль профиля s(x,t) и т. п.
Многомерные сигналы могут иметь различное представление по своим координатам. Так, полный акустический сигнал сейсмического профиля дискретен по пространству (точкам расположения приемников) и непрерывен по времени.
В общем случае многомерный сигнал может рассматриваться, как упорядоченная совокупность одномерных сигналов. С учетом этого при анализе и обработке сигналов многие принципы и практические методы обработки одномерных сигналов, математический аппарат которых развит достаточно глубоко, распространяются и на многомерные сигналы. Физическая природа сигналов для математического аппарата их обработки значения не имеет. Вместе с тем обработка многомерных сигналов имеет свои особенности и может существенно отличаться от одномерных сигналов в силу большего числа степеней свободы. Так, при дискретизации многомерных сигналов имеет значение не только частотный спектр сигналов, но и форма растра дискретизации. Что касается порядка размерности многомерных сигналов, то ее увеличение выше двух не изменяет принципов и методов анализа данных и сказывается только на техническом усложнении вычислений. Учитывая эти факторы, при рассмотрении общей теории анализа, преобразований и обработки сигналов ограничимся, в основном, одно- и двумерными сигнальными функциями, а в качестве универсальной независимой переменной будем использовать, как правило, переменную t для одномерных сигналов и переменные x, t или x, y для двумерных сигналов, безотносительно к их физическому содержанию.
1.2. Типы сигналов
Аналоговый сигнал является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения независимой переменной. Источниками аналоговых сигналов, как правило, являются физические процессы и явления, непрерывные в своем развитии (динамике изменения значений определенных свойств) во времени, в пространстве или по любой другой независимой переменной, при этом регистрируемый сигнал подобен (аналогичен) порождающему его процессу. Пример математической записи конкретного аналогового сигнала:
y(t) = 4.8 exp[-(t-4)2/2.8]. Пример графического отображения данного сигнала приведен на рис. 1.2.1, при этом как числовые величины самой функция, так и ее аргументов, могут принимать любые значения в пределах некоторых интервалов y1 y y2, t1 t t2. Если интервалы значений сигнала или его независимых переменных не ограничиваются, то по умолчанию они принимаются равными от - до +. Множество возможных значений сигнала образует континуум - непрерывное пространство, в котором любая точка сигнала может быть определена с точностью до бесконечности.
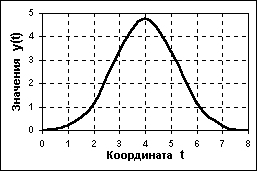
Рис. 1.2.1. Графическое отображение сигнала y(t) = 4.8 exp[-(t-4)2/2.8].
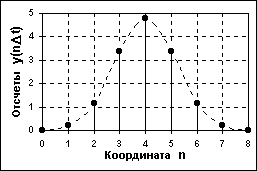
Дискретный сигнал по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента. По множеству своих значений он является конечным (счетным) и описывается дискретной последовательностью y(nt), где y1 y y2, t - интервал между отсчетами (интервал дискретизации сигнала), n = 0,1,2,..., N – нумерация дискретных значений отсчетов. Если дискретный сигнал получен дискретизацией аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам nt.
Пример дискретизации аналогового сигнала, приведенного на рис. 1.2.1, представлен на рис. 1.2.2. При t = const (равномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначением y(n). В технической литературе в обозначениях дискретизированных функций иногда оставляют прежние индексы аргументов аналоговых функций, заключая последние в квадратные скобки - y[t].
При неравномерной дискретизации сигнала обозначения дискретных последовательностей (в текстовых описаниях) обычно заключаются в фигурные скобки - {s(ti)}, а значения отсчетов приводятся в виде таблиц с указанием значений координат ti. Для коротких неравномерных числовых последовательностей применяется и следующее числовое описание: s(ti) = {a1, a2, ..., aN}, t = t1, t2, ..., tN.