Файл: Лабораторная работа 7 Определение момента инерции тел с помощью маятника Максвелла Студент группы рги20 Жуйков А. С.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 222

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное бюджетное образовательное учреждение высшего образованияСанкт-Петербургский горный университетотчётЛабораторная работа №7«Определение момента инерции тел с помощью маятника Максвелла»Выполнил: Студент группы РГИ-20 Жуйков А.С.Проверил доцент кафедры ОТФ Кожокарь М.Ю.Дата:29.09.2020Санкт-Петербург 20201)Цель работы – изучение маятника Максвелла и определение с его помощью момента инерции твёрдых тел.2)Основные теоретические данные: Явления, изучаемые в работе: Закон сохранения энергииОпределения:Момент инерции системы (тела) относительно оси вращения - это скалярная величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.Твёрдое тело – агрегатное состояние вещества, характеризующееся стабильностью формы и характером теплового движения атомов, совершающих малые колебания около положений равновесия.Основные физические законы:Закон сохранения энергииМомент инерции твердого тела в данной работе рассчитывается по формуле выведенной на основе закона сохранения энергии.E = En = mgh - полная энергия маятника в начальном положении (при закреплении его на верхнем кронштейне), численно равная его потенциальной энергии.E = Eк = Eкn + Eквр = 0,5mv2 + 0,5Jw2 - полная энергия маятника в нижней точке движения, равная сумме кинетических энергий поступательного и вращательного движений.3)Схема установки

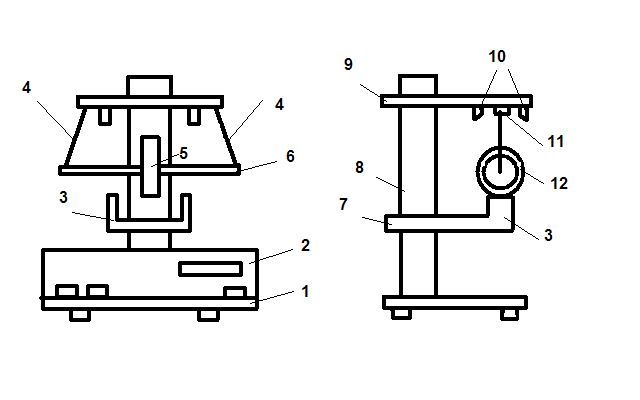
1. Основание установки.
7. Подвижный нижний кронштейн.

2. Электронный секундомер.
8. Колонка.

3. Фотоэлектрический датчик.
9. Верхний кронштейн, прикрепленный неподвижно к колонке X

4. Нити.
10. Электромагнит.

5. Диск маятника.
11.Фотоэлектрический датчик.

6. Ось маятника.
12. Сменные кольца.
4)Основные расчётные формулы:

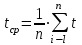  • - среднее значение времени падения маятника: n- количество падений, ti – время падения

  • m=mo+mд+mk - общая масса установки; mo - масса оси, mд – масса диска, mk – масса кольца

  • Jt=Jо+Jк+Jд – теоретическое значение момента инерции маятника

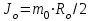  1. - момент инерции оси маятника; mo – масса оси, Ro – радиус оси

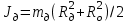  2. - момент инерции диска; mд – масса диска, Rд – радиус диска, Ro – радиус оси

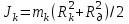  3. - момент инерции кольца, надетого на диск; mk – масса кольца, Rk – радиус кольца, Rд – радиус диска

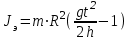  • - экспериментальное значение момента инерции маятника; m – масса маятника, R – радиус оси, кольца и диска вместе, g – ускорение свободного падения, t – время падения, h – пройденное телом расстояние
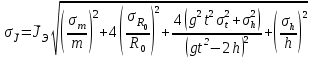
5)Формулы погрешности косвенных измерений:6)Таблица №1 «Время падения и момент инерции»
t1
t2
t3
Jэ1
Jэ2
Jэ3
Jт1
Jт2
Jт3




С
с
С
Кг*м

*10-4
Кг*м

*10-4
Кг*м

*10-4
Кг*м

*10-4
Кг*м

*10-4
Кг*м

*10-4

1
2,279
2,136
2,165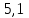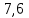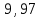






7,2
10,15
13,18

2
2,038
2,147
2,179

3
2,040
2,153
2,173

4
2,038
2,117
2,182

5
2,054
2,116
2,159

6
2,048
2,115
2,149

7
2,054
2,128
2,192

8
2,041
2,127
2,166

9
2,052
2,130
2,188

10
2,059
2,120
2,192
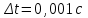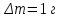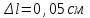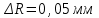
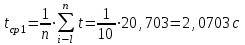
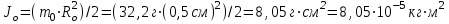
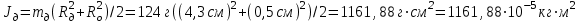
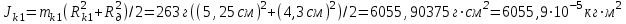
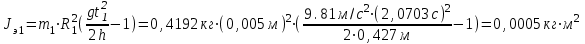
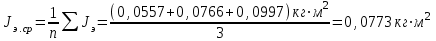
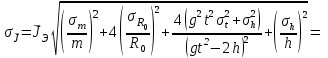
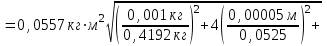
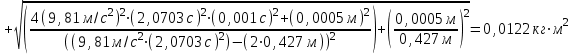
7)Пример вычислений:А)Исходные данные:g=9,81м/c2; mo=32,2г; mд=124г; mk1=263г; mk2=392г; mk3=522г; h=42,7см; Ro=0,5см; Rд=4,3см; Rk1=5,25см; Rk2=5,23см; Rk3=5,25смБ)Погрешности прямых измерений: ; ; ; В)Вычисление величин и косвенных погрешностей:m1=mo+mд+mk1 =32,2+124+263=419,2гJt1=Jо+Jк1+Jд=0,805кг*м2+116,188кг*м2+605,59кг*м2=722,583*10-5кг*м2Окончательные результаты:Jt=7,2*10-4кг*м2 Jt2=10,15*10-4кг*м2Jt3=13,18*10-4кг*м2
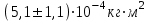
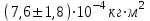
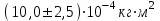
Jэ1=Jэ2=Jэ3=Вывод: В результате проведенного опыта было найдено 3 значения момента инерции для сменных колец различной массы, оси и диска, т.е. для различных масс маятника Максвелла. Из результатов опыта видно, что с увеличением массы маятника увеличивается и момент инерции, т.е. существует прямая зависимость между этими величинами. Несоответствия опытных значений момента инерции с теоретическими

, связаны, прежде всего с разными внешними факторами, появившимися в течении опыта, а также с погрешностями измерительных приборов, применявшихся в данном опыте.

Смотрите также файлы