ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 616
Скачиваний: 36
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Расчётно-графическое задание по дисциплине
ФИЗИКА
Вариант 10
| 1.7 | 2.7 | 3.1 | 4.2 | 5.3 | 6.5 | 7.6 | 8.7 | 9.7 | 10.8 |
| | | | | | | | | | |
| 11.1 | 12.8 | 13.1 | 14.10 | 15.5 | 16.2 | 17.3 | 18.10 |
| | | | | | | | |
Факультет: АВТФ Преподаватель: Штыгашев А.А.
Группа: АВТ-209
Студент: Еранский Клим
Новосибирск
2023
Задача 1.7
Постановка задачи: Две абсолютно гладкие стальные плиты высотой 1,00 м помещены рядом и образуют щель шириной 5 см. В щель попадает горизонтально движущийся со скоростью 1,5 м/с стальной шарик диаметром 5 мм. Направление шарика перед попаданием в щель перпендикулярно щели. Сколько раз шарик ударится о стенки, пока не достигнет пола? Считать абсолютно упругим удар шарика о стенку и для каждого столкновения выполняется закон отражения. Построить график скорости движения шарика и график траектории движения шарика.
Д
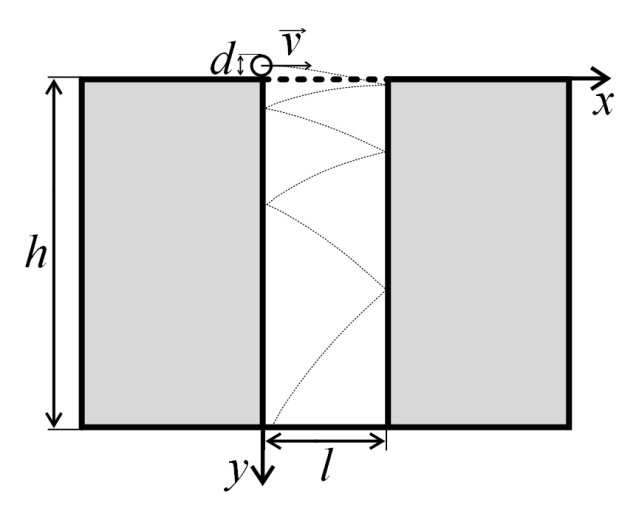
ано: Решение
h = 1 м◦
l = 0.05 м
v0 = 1.5 м/с
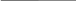d = 0.005 мN = ?
Рисунок 1 ‑ Предполагаемая траектория шарика (постановочный рисунок)
Математическая модель
Движение шарика по параболе можно разложить на движение по горизонтали и вертикали (Рисунок 1). В горизонтальном направлении движение шарика равномерное и прямолинейное. В вертикальном направлении движение шарика равноускоренное.
Для проекций скорости в любой момент времени, движения можно записать следующие уравнения
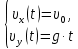,(1)где
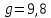м/с2 – ускорение свободного падения.Движение шарика вдоль оси х от начала движения до удара о стенку:
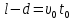, (2)где
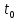– время удара шарика о стенку.Расстояние
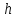, за которое шарик опускается в вертикальном направлении, за время полета шарика t. 
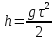, (3)где
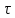– время движения шарика в момент удара о пол.Число ударов шарика о стенки:
. (4)Решаем систему (2)-(4) и получаем конечную формулу числа ударов шарика об стенку:
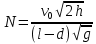. (5))Подставляем численные значения в (5) и получаем
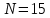.Графическая часть
Скорость движения шарика из (1) получаем
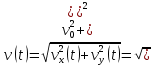. (6)Построим график скорости движения шарика (Рисунок 2) по (6) и траекторию движения шарика(Рисунок 3).
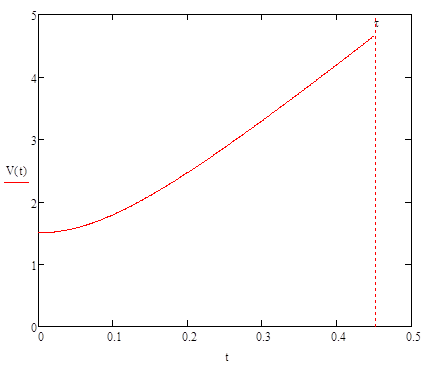
Рисунок 2 – График скорости движения шарика. По оси ординат скорость в м/с, по оси абсцисс время в с
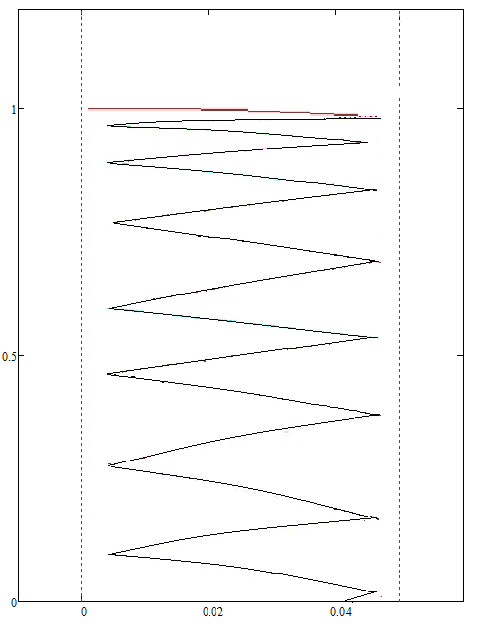
Рисунок 3 – Траектория движения шарика. По оси ординат высота в
м, по оси абсцисс ширина в м
Анализ решения: Сравниваем расчетную величину ударов шарика о стенку с решением, найденным графически на Рисунке 3, убеждаемся, что решение найдено правильно.
Ответ:
Задача 2.7.
Постановка задачи: Глыба льда массой 40 кг скатывается с покрытой коркой льда наклонной крыши и падает с высоты 35 м. Определить безопасную зону, если известно, что длина пути пройденного телом по скату составляет 10 м, угол ската крыши
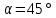. Коэффициент трения 
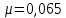(при -20 0С). Построить график траектории движения глыбы льда.
Д
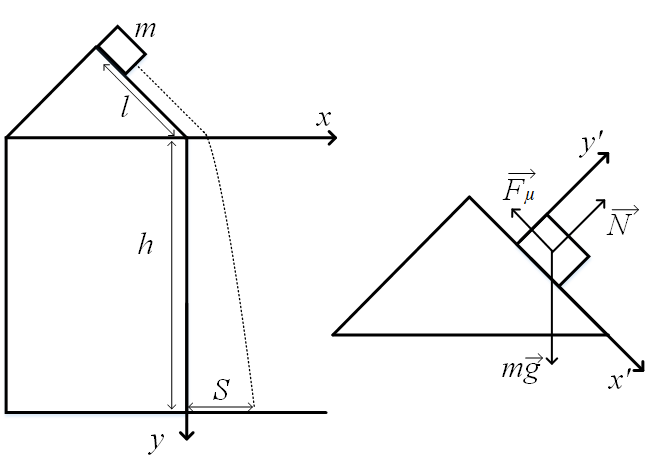ано: Решениеm = 40 кг
h = 35 м
l = 10 м
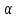=45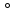
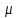= 0.065 S = ?
Рисунок 1 – Постановочный рисунок
Математическая модель: уравнения движения глыбы льда по II закону Ньютона:
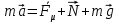, (1)где
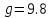м/с2 – ускорение свободного падения, а – ускорение глыбы льда.Найдем проекции сил на оси координат:
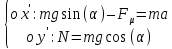, (2)Сила трения равна
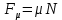. (3)Скорость глыбы в момент падения с крыши, с учётом того, что глыба льда до начала падения покоилась:
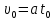, (4)где
– время отрыва льдины от крыши.Расстояние, которое проскальзывает лёд по крыше:
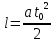. (5)Решая систему (2)-(5) получаем скорость льдины в момент начала падения с крыши:
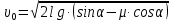. (6)Для удобства стразу посчитаем скорость льдины в момент начала падения:
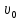= 11.4 м/с.Глыба льда, после соскальзывания с крыши, движется с постоянным ускорением
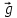и начальной скоростью 
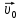.Запишем уравнения движения глыбы:
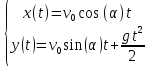. (7)Необходимо найти время падения льда с высоты крыши. Для этого запишем (7) в момент падения:
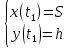, (8)где
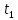– время падения льда с крыши. Подставляем (8) в (7) и находим время падения из квадратного уравнения (отрицательный корень не учитываем):
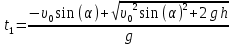. (9)Подставляем (9) и (6) в (7) и получаем формулу для безопасного расстояния:
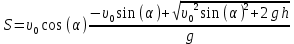. (10)Подставляем численные данные в формулу (10) и получаем длину безопасной зоны
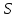= 15.9 м.Графическая часть: Запишем уравнения движения глыбы льда в стандартных декартовых координатах:
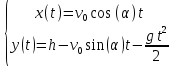. (11)Построим траекторию движения глыбы с самого начала её соскальзывания по формуле (11) на Рисунке 2.
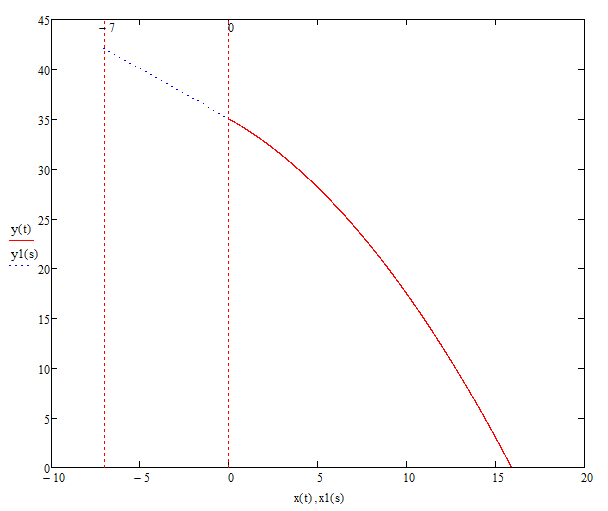
Рисунок 2 – Траектория движения глыбы. По оси ординат высота в метрах, по оси абсцисс ширина в метрах.
Анализ результатов: Сравниваем расчётное значения безопасной зоны с решением, найденным графически на Рисунке 2, и делаем вывод, что решение найдено верно.
Ответ:
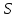
= 15.9 м.
Задача 3.1
Постановка задачи: Легендарный железнодорожный транспортер ТМ-1-180 с орудием обеспечивал снаряду массой 97,5 кг начальную скорость 920 м/с. Масса транспортера 160 тонн (Амирханов Л.И. Морские пушки на железной дороге. СПб: Иванов и Лещинский, 1994. –64 с.). Из орудия производят выстрел вдоль железнодорожного пути. Определить на какое расстояние S откатится транспортер, если предположить, что вышло из строя противооткатное устройство. Принять, что угол возвышения ствола равен 45 градусов, коэффициент трения равен 0,02. Построить график S = S(α) в диапазоне углов от 0 до 500.
Дано: Решениеm
= 97,5 кг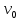
=920 м/сα = 450
M= 160 т
= 0,02 S = ?
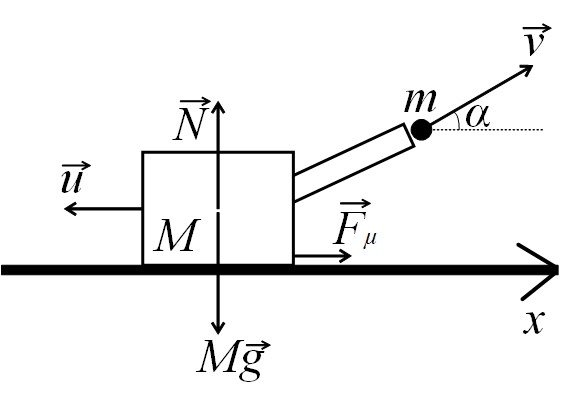
Рисунок 1 ‑ Постановочный рисунок
Математическая модель:
В момент выстрела на транспортёр действуют силы трения, реакции опоры и тяжести:
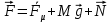, (1)где
м/с2 – ускорение свободного падения,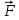 
- равнодействующая всех сил, действующих на транспортёр.Спроецируем (1) на ось х и применим 2 закон Ньютона:
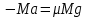, (2)где
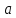– ускорение транспортёра.Пройденный путь транспортёра после выстрела равен:
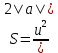, (3)где
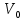– скорость транспортёра в момент выстрела.Для нахождения начальной скорости транспортёра в момент выстрела распишем проекцию на ось х закона сохранения импульса:
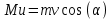. (4)Решаем систему (2)-(4) и получаем пройденный транспортёром путь:
.
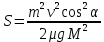