ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 618
Скачиваний: 36
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(5)
Подставляем численные данные в (5) и получаем перемещение транспортёра S = 0.4 м.
Графическая часть.
Построим графики зависимости перемещение транспортёра в зависимости от угла наклона пушки по формуле (5) на Рисунке 2.
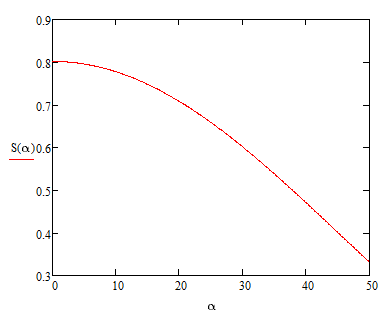
Рисунок 2 ‑ График зависимости перемещения транспортёра в зависимости от угла наклона пушки. По оси ординат расстояние в м, по оси абсцисс угол наклона в градусах.
Анализ решения: Сравниваем расчётное перемещения пушки при 45
с решением на Рисунке 2 и делаем вывод, что решение найдено верно.
Ответ: S = 0.4 м.
Задача 4.2.
Постановка задачи: Два одинаковых цилиндра одновременно начали движение. Первый цилиндр падает свободно, а второй цилиндр падает, раскручивая предварительно намотанную тонкую гибкую нерастяжимую ленту, массой которой можно пренебречь по сравнению с массой цилиндра, свободный конец ленты закреплен. С какой скоростью упадут цилиндры, если начальная высота равна 20 м. Постройте графики высоты цилиндров от времени и определите момент времени, когда расстояние между ними составляет 1 м.
Дано: Решение
h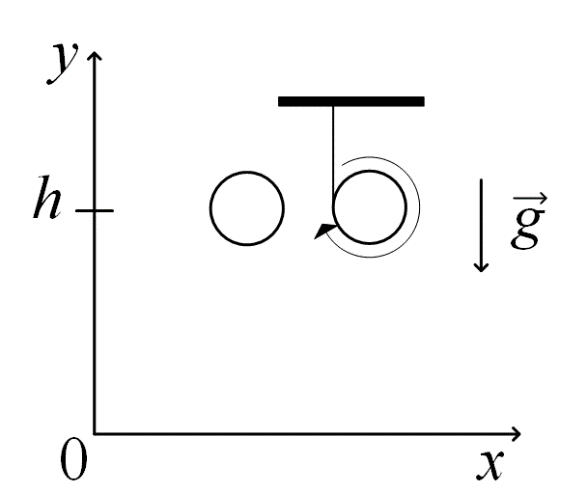
= 20 м
=1 м
V1 = ?
V2 = ?
= ?
Рисунок 1 ‑Постановочный рисунок
Математическая модель: первый цилиндр падает свободно, поэтому его ускорение равно ускорению свободного паденияg. Зависимость высоты первого цилиндра от времени t:
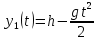(1)
Для первого цилиндра запишем закон сохранения энергии:
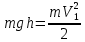, (2)
где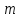
– масса цилиндров. Из формулы (2) выражаем конечную скорость первого цилиндра:
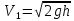
. (3)
Запишем проекцию на ось Oy II Закон Ньютона для второго цилиндра:
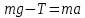, (4)
где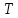
– сила натяжения нити, a–линейное ускорение второго цилиндра.
По основному закону динамики вращательного движения тела момент сил, действующих на второй цилиндр:
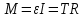, (5)
где R – радиус цилиндра.
Так как нить закреплена и натянута по условию, ускорение точки касания нити и цилиндра равно 0:
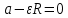. (6)
Момент инерции цилиндра:
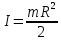. (7)
Решаем систему (4)-(7) получаем ускорение второго цилиндра:
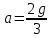. (8)
Тогда конечная скорость второго цилиндра из закона сохранения энергии:
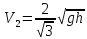. (9)
Зависимость высоты второго цилиндра от времени t:
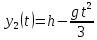(10)
Тогда расстояние в высоте между цилиндрами :
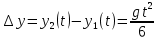(11)
Выразим время, при котором расстояние между цилиндрами будет
:
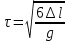. (12)
Подставляем численные значения в (3), (9) и (12) и получаем конечные скорости первого цилиндра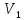
= 19.8 м/с, второго цилиндра 
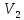= 16.2 м/с, и время = 0.78 c, при котором расстояние между цилиндрами будет =1 м.
Графическая часть: Построим графики высот цилиндров от времени по формулам (1) и (10), также разницу между высотами по формуле (11) на Рисунке 2.
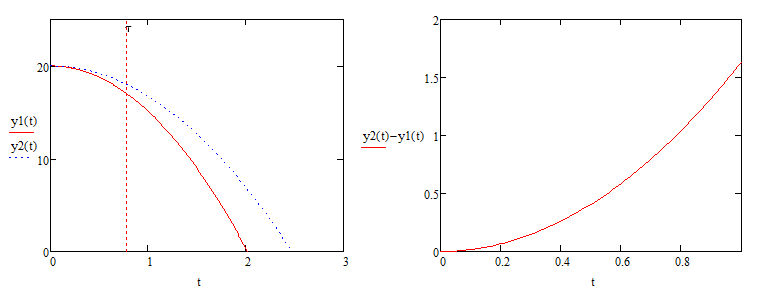
Рисунок 2 ‑ Графики высот цилиндров от времени (слева) и разницу между высотами (справа). По оси ординат высота в метрах, по оси абсцисс время в секундах.
Анализ решения: Сравниваем расчётное время, при котором расстояние между цилиндрами 1 м, и решением, найденным графически на Рисунке 2, и делаем вывод, что решение найдено верно.
Ответ:
= 19.8 м/с, 
= 16.2 м/с, = 0.78 c.
Задача 5.3.
Постановка задачи: Поезд движется по закруглению радиусом 500 м. Ширина железнодорожной колеи 152.4 см. Наружный рельс расположен на 12 см выше внутреннего. При какой скорости движения поезда на закруглении колеса не оказывают бокового давления на рельсы? Построить поясняющий рисунок и указать все необходимые детали (векторы, углы).
Дано: Решение
R = 500 м
D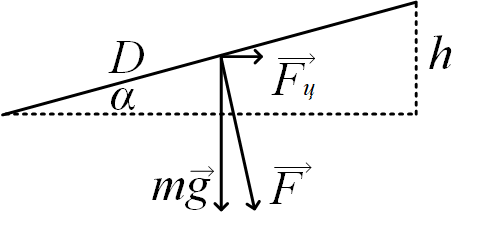
= 1.524 м
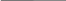h=0.12 м
v = ?
Рисунок 1 – Рельс и действующие на него силы
Математическая модель: на рельсы действуют сила тяжести поезда и центробежная сила:
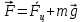, (1)
где
м/с2 – ускорение свободного падения.
Для того чтобы на рельсы не оказывалось бокового давления, необходимо, чтобы результирующая всех сил, действующих на рельсы, была перпендикулярна рельсам:
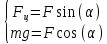, (2)
где
– угол между рельсом и горизонтальной поверхностью.
Центробежная сила равна:
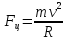. (3)
Решаем систему (2),(3) и, применяя формулу tg(arcsin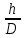
), получаем значение скорости поезда, при которой на закруглении колеса не оказывают бокового давления на рельсы:
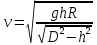.. (4)
Подставляем численные значения в (4) и получаем скорость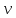
= 19.7 м/с.
Анализ результатов: Несмотря на сложное конусовидное строение колёс поездов, для уменьшения бокового воздействия на рельсы от поездов необходимо внешний от радиуса поворота рельс поднимать на некоторую высоту для компенсации центробежной силы. В этом случае на рельсы действует меньшая боковая сила, что увеличивает их долговечность.
Ответ:
= 19.7 м/с.
Подставляем численные данные в (5) и получаем перемещение транспортёра S = 0.4 м.
Графическая часть.
Построим графики зависимости перемещение транспортёра в зависимости от угла наклона пушки по формуле (5) на Рисунке 2.
Рисунок 2 ‑ График зависимости перемещения транспортёра в зависимости от угла наклона пушки. По оси ординат расстояние в м, по оси абсцисс угол наклона в градусах.
Анализ решения: Сравниваем расчётное перемещения пушки при 45
с решением на Рисунке 2 и делаем вывод, что решение найдено верно.Ответ: S = 0.4 м.
Задача 4.2.
Постановка задачи: Два одинаковых цилиндра одновременно начали движение. Первый цилиндр падает свободно, а второй цилиндр падает, раскручивая предварительно намотанную тонкую гибкую нерастяжимую ленту, массой которой можно пренебречь по сравнению с массой цилиндра, свободный конец ленты закреплен. С какой скоростью упадут цилиндры, если начальная высота равна 20 м. Постройте графики высоты цилиндров от времени и определите момент времени, когда расстояние между ними составляет 1 м.
Дано: Решениеh
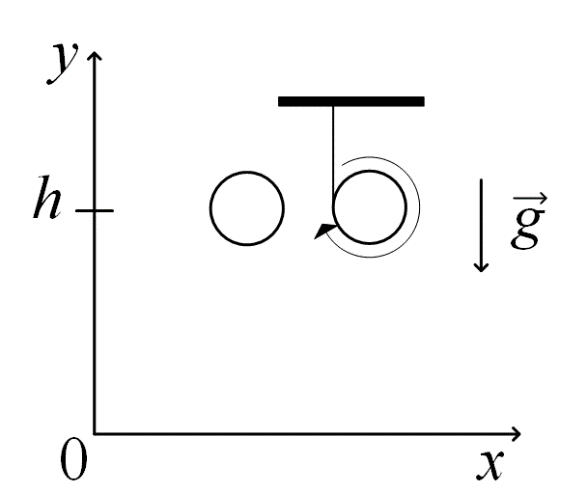= 20 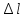м =1 мV1 = ?
V2 = ?
= ?Рисунок 1 ‑Постановочный рисунок
Математическая модель: первый цилиндр падает свободно, поэтому его ускорение равно ускорению свободного паденияg. Зависимость высоты первого цилиндра от времени t:
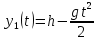(1)Для первого цилиндра запишем закон сохранения энергии:
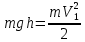, (2)где
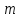– масса цилиндров. Из формулы (2) выражаем конечную скорость первого цилиндра: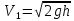
. (3)
Запишем проекцию на ось Oy II Закон Ньютона для второго цилиндра:
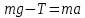, (4)где
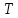– сила натяжения нити, a–линейное ускорение второго цилиндра.По основному закону динамики вращательного движения тела момент сил, действующих на второй цилиндр:
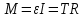, (5)где R – радиус цилиндра.
Так как нить закреплена и натянута по условию, ускорение точки касания нити и цилиндра равно 0:
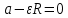. (6)Момент инерции цилиндра:
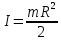. (7)Решаем систему (4)-(7) получаем ускорение второго цилиндра:
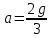. (8)Тогда конечная скорость второго цилиндра из закона сохранения энергии:
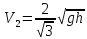. (9)Зависимость высоты второго цилиндра от времени t:
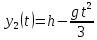(10)Тогда расстояние в высоте между цилиндрами :
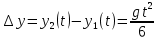(11)Выразим время, при котором расстояние между цилиндрами будет
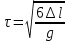: . (12)Подставляем численные значения в (3), (9) и (12) и получаем конечные скорости первого цилиндра
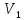= 19.8 м/с, второго цилиндра 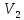= 16.2 м/с, и время = 0.78 c, при котором расстояние между цилиндрами будет =1 м. Графическая часть: Построим графики высот цилиндров от времени по формулам (1) и (10), также разницу между высотами по формуле (11) на Рисунке 2.
Рисунок 2 ‑ Графики высот цилиндров от времени (слева) и разницу между высотами (справа). По оси ординат высота в метрах, по оси абсцисс время в секундах.
Анализ решения: Сравниваем расчётное время, при котором расстояние между цилиндрами 1 м, и решением, найденным графически на Рисунке 2, и делаем вывод, что решение найдено верно.
Ответ:
= 19.8 м/с, = 16.2 м/с, = 0.78 c.Задача 5.3.
Постановка задачи: Поезд движется по закруглению радиусом 500 м. Ширина железнодорожной колеи 152.4 см. Наружный рельс расположен на 12 см выше внутреннего. При какой скорости движения поезда на закруглении колеса не оказывают бокового давления на рельсы? Построить поясняющий рисунок и указать все необходимые детали (векторы, углы).
Дано: РешениеR = 500 м
D
= 1.524 м h=0.12 мv = ?
Рисунок 1 – Рельс и действующие на него силы
Математическая модель: на рельсы действуют сила тяжести поезда и центробежная сила:
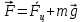, (1)где
м/с2 – ускорение свободного падения.Для того чтобы на рельсы не оказывалось бокового давления, необходимо, чтобы результирующая всех сил, действующих на рельсы, была перпендикулярна рельсам:
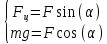, (2)где
– угол между рельсом и горизонтальной поверхностью.Центробежная сила равна:
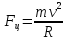. (3)Решаем систему (2),(3) и, применяя формулу tg(arcsin
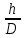), получаем значение скорости поезда, при которой на закруглении колеса не оказывают бокового давления на рельсы: 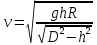.. (4)Подставляем численные значения в (4) и получаем скорость
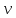= 19.7 м/с.
Анализ результатов: Несмотря на сложное конусовидное строение колёс поездов, для уменьшения бокового воздействия на рельсы от поездов необходимо внешний от радиуса поворота рельс поднимать на некоторую высоту для компенсации центробежной силы. В этом случае на рельсы действует меньшая боковая сила, что увеличивает их долговечность.
Ответ:
= 19.7 м/с.