ПК 1.1 Синтезирование цифрового устройства q=1 если d=0 d=9 d=12

1. 
   Создание схемы входов и выхода устройства.
   

d1

1



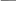
d2

2

K4

q



d3

3




Рисунок 1.1 Схема входов и выхода устройства

2. 
   Создание таблицы истинности
   

d0	d1	d2	d3	Q
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

---

Рисунок 1.2 Таблица истинности

3. 
   Пишем формулу исходя из таблицы
   

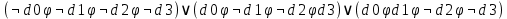
Рисунок 1.3 Формула

4. 
   Создаем карту Карно
   

d0d1 /d2d3	00	01	11	10
00	1	0	0	0
01	0	0	0	0
11	1	0	0	0
10	0	1	0	0

Рисунок 1.4 Таблица Карно

5. 
   Создаем схему по формуле
   

Рисунок 1.5 Схема подключения цифрового устройства

Нам надо синтезировать резервный счётчик с модулем счёта 3 на триггерах типа D, направление счёта управляет сигнал m


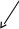
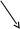
n







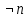
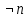
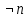
n

Q2

Q0

Q1

---

n


n=1 вычитание q0=00,q1=01,q1=10

n=0 сложение

n	q(t)		Q(t+1)		D
	q1	q0	q1	q0	q1	q0
0	0	0	0	1	0	1
0	0	1	1	0	1	0
0	1	0	0	0	0	0
1	0	0	1	0	1	0
1	1	0	0	1	0	1
1	0	1	0	0	0	0

1: d1=

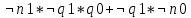
2: d0=



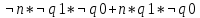
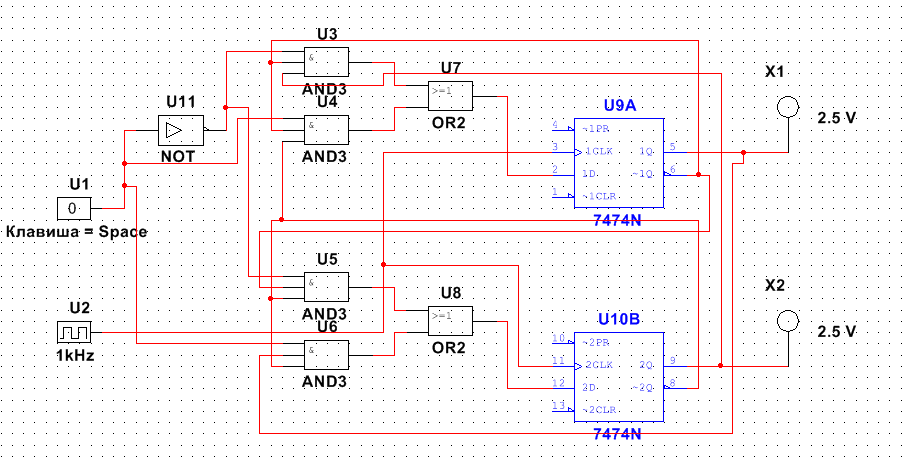
Рисунок. Условно графические обозначение элементов

ПК 1.2 Основные сведенья о ЛЭ

Определение истинности или ложности составного высказывания зависит от того, являются ли истинными или ложными простые высказывания, входящие в его состав, а также от той логической операции, которая их связывает.

Составное высказывание А И В, образованное в результате объединения двух простых высказываний А и B логической операцией И, истинно тогда и только тогда, когда А и В одновременно истинны

Операцию И называют логическим умножением. Равенства 1 · 1 = 1, 1 · 0 = 0, 0 · 1 = 0, 0 · 0 = 0, верные для обычного умножения, верны и для логического умножения.

Представим таблицу истинности для логической операции 

---

И:

 

А	В	А И В
1	1	1
0	1	0
1	0	0
0	0	0

Если хотя бы одно из простых высказываний, связанных операцией И, будет ложным, то и составное высказывание будет ложным.

Для записи логической операции И используют следующие обозначения: A ИB, AANDB, A · B, A *B, A^∧B, A & B.

Логическая операция ИЛИ

Составное высказывание А ИЛИ В,образованное в результате объединения двух простых высказываний А и B логической операцией ИЛИ, ложно тогда и только тогда, когда А и В одновременно ложны

Другими словами, составное высказывание А ИЛИ В будет истинным, если истинно хотя бы одно из двух составляющих его простых высказываний

Таблица истинности для логической операции ИЛИ имеет следующий вид:

А	В	А ИЛИ В
1	1	1
0	1	1
1	0	1
0	0	0

Операцию ИЛИ называют логическим сложением. Равенства 1 + 0 = 1, 0 + 1 = 1, 0 + 0 = 0, верные для обычного сложения, верны и для логического сложения.

Для записи логической операции ИЛИ можно использовать следующие выражения: AИЛИB, A OR B, A + B, A^∨B, A | B.

Если в логическом выражении присутствует несколько логических операций, то важно определить порядок их выполнения. Наивысшим приоритетом обладает операция 

---

НЕ. Логическая операция И, т. е. логическое умножение, выполняется раньше операции ИЛИ — логического сложения

Для изменения порядка выполнения логических операций используют скобки: в этом случае сначала выполняются операции в скобках, а затем — все остальные.

Логические операции И и ИЛИ подчиняются переместительному закону:

AИB = BИA;

AИЛИB = BИЛИA.

Чтобы определить значение составного логического выражения, иногда достаточно знать значение только одного простого высказывания.

Так, если в составном высказывании с операцией И значение хотя бы одного простого высказывания является ложным, то и значение составного высказывания будет ложным. Если в составном высказывании с операцией ИЛИ значение хотя бы одного простого будет истинным, то и значение составного высказывания будет истинным

«НЕ» - логический элемент, выполняющий над входными данными операцию логического отрицания. Данный элемент, имеющий один выход и только один вход, называют еще инвертором, поскольку он на самом деле инвертирует (обращает) входной сигнал. На рисунке приведено условное обозначение логического элемента «НЕ».



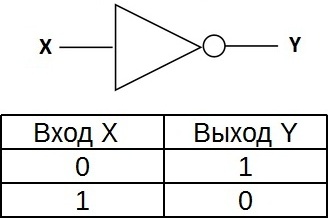
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.

На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.

Триггеры — класс электронных устройств, обладающих способностью длительно находиться в одном из двух устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам — их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время. Отличительной особенностью триггера как функционального устройства является свойство запоминания двоичной информации. Под памятью триггера подразумевают способность оставаться в одном из двух состояний и после прекращения действия переключающего сигнала. Приняв одно из состояний за «1», а другое за «0», можно считать, что триггер хранит (помнит) один 

---

Смотрите также файлы

• История математики.ppt

• Наблюдение в оптическом диапазоне и применяемые для этого средства.docx

• Негосударственное образовательное частное учреждение высшего образования московский финансовопромышленный университетсинергия.docx

• Отчет по учебной практике (наименование вида практики).docx

• Отчет по производственной практикЕ (вид практики) Педагогическая (тип практики) 3 семестр.docx