ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| |
| (код и наименование направления подготовки / специальности) |
| |
| (направленность (профиль) / специализация) |
Практическое задание №___
по учебному курсу «»
(наименование учебного курса)
Вариант ____ (при наличии)
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
| № п/п | Задача | Ответ |
| 1. | Вычислить объём тела, заданного представленными уравнениями, используя его поперечные сечения: | |
| Условие задачи:  |  | |
| Чертёж:  |
| № п/п | Задача | Ответ |
| 1. | Подробное решение: Очевидно, что максимальное значение 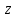 имеет при имеет при 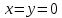 и равно и равно 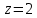 . Следовательно, тело, объем которого необходимо вычислить, находится между плоскостями . Следовательно, тело, объем которого необходимо вычислить, находится между плоскостями  и и 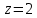 . .Поперечным сечением в решаемой задаче является эллипс, уравнение которого выразим из заданного по условию. 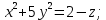 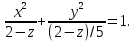 Площадь эллипса вычисляется по формуле: 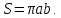  тогда тогда Объем тела, заключенного между двумя плоскостями, в случае, если площадь сечения, проведенная перпендикулярно к оси Oz, есть известная функция от z, вычисляется по формуле: 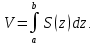 Тогда искомый объем: 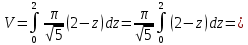 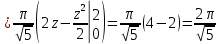 | |
| № п/п | Задача | Ответ |
| 2. | Вычислить объём тела, образованного вращением вокруг оси  фигуры, заданной представленными линиями: фигуры, заданной представленными линиями: | |
| Условие задачи: 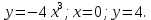 | 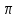 | |
| Чертёж: Изобразим в декартовой системе координат все три линии, заданные в условии. 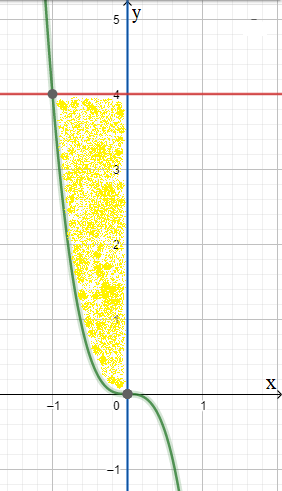 Желтым цветом закрашена фигура, которую необходимо вращать вокруг оси Ох. |
| № п/п | Задача | Ответ |
| 2. | Подробное решение: Объем тела, образованного вращением вокруг оси Ох, вычисляется по формуле: 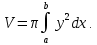 Верхний предел интегрирования известен и равен 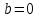 . .Нижний предел найдем из уравнений, заданных в условии:  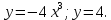  Следовательно,  . Тогда . Тогда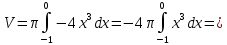 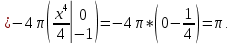 | |