Файл: Эмпирическая функция распределения. Полигон и гистограмма. В результате изучения темы студент должен.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 68
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Эмпирическая функция распределения. Полигон и гистограмма. | В результате изучения темы студент должен: - знать геометрическое изображение выборки: полигон и гистограмма, эмпирическую функцию распределения выборки, числовые характеристики выборки | [1], [3], [4] |
| Статистические оценки параметров распределения | В результате изучения темы студент должен: - знать понятие точечной оценки - знать понятие интервальной оценки | [1], [3], [4] |
Перечень информационного обеспечения:
основной и дополнительной литературы, учебно-методических пособий,
электронных ресурсов
| № п/п. | Автор | Наименование | Издательство | Год издания |
| 1 | И. И. Валуцэ, Г. Д. Дилигул | Математика для техникумов | М. : Наука | 1989 |
| 2 | Данко П.Е., Попов А.Г., Кожевникова Т.Я. | Высшая математика в задачах и упражнениях | М. : «Высшая школа» | 1999 |
| 3 | А. Г. Мякишев | Теория вероятностей. Элективный курс | М. :Издательство: Илекса | 2012 |
| 4 | М. С. Спирина, П. А. Спирин | Теория вероятностей и математическая статистика: учебник | М. : ИЦ "Академия" | 2014 |
| 5 | М. С. Спирина, П. А. Спирин | Теория вероятностей и математическая статистика. Сборник задач: учебное пособие | М. : ИЦ "Академия" | 2014 |
Тема лекции: Математическая статистика
План:
-
Основные понятия математической статистики -
Графическое изображение выборки -
Точечные оценки параметров распределения
-
Основные понятия математической статистики
На практике функция распределения случайной величины бывает неизвестна и ее определяют по результатам наблюдений или, как говорят, по выборке. Выборкой объема n для случайной величины называется последовательность независимых наблюдений этой величины, где
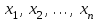 – совокупность значений, принятых независимыми случайными величинами
– совокупность значений, принятых независимыми случайными величинами 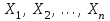 , имеющими тот же закон распределения
, имеющими тот же закон распределения 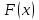 , что и величина X. В этом случае говорят, что выборка
, что и величина X. В этом случае говорят, что выборка 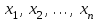 взята из генеральной совокупности величины X, а под законом распределения генеральной совокупности понимают закон распределения случайной величины X. Значения
взята из генеральной совокупности величины X, а под законом распределения генеральной совокупности понимают закон распределения случайной величины X. Значения 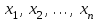 называют выборочными значениями или вариантами. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом. Число, указывающее, сколько раз наблюдается данная варианта, называется частотой варианты, а отношение частоты варианты к объему выборки – относительной частотой.
называют выборочными значениями или вариантами. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом. Число, указывающее, сколько раз наблюдается данная варианта, называется частотой варианты, а отношение частоты варианты к объему выборки – относительной частотой.Если
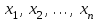 – вариационный ряд, а x – произвольное число, и nx – количество выборочных значений, меньших x, то
– вариационный ряд, а x – произвольное число, и nx – количество выборочных значений, меньших x, то 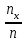 – частота попадания выборочных значений левее точки x в данной выбоке объема n, т. е. частота события
– частота попадания выборочных значений левее точки x в данной выбоке объема n, т. е. частота события 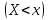 .
.Эта частота является функцией от x и называется эмпирической функцией распределения случайной величины X, полученной по данной выборке. Если обозначить эту функцию через
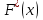 , то по определению
, то по определению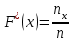 .
.Эмпирическая функция распределения
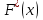 обладает всеми свойствами функции распределения
обладает всеми свойствами функции распределения 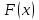 . Так как частота события в
. Так как частота события в
n независимых опытах является оценкой вероятности этого события, то значение эмпирической функции распределения в точке x есть оценка вероятности события
 , то есть оценка теоретической функции распределения
, то есть оценка теоретической функции распределения  :
: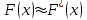 .
.Статистическим рядом распределения называется таблица, которая содержит вариационный ряд и соответствующие частоты или относительные частоты членов этого ряда (табл. 1).
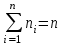 ,
,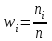 ,
, 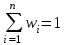 .
.Таблица 1 Таблица 2
| x1 | x2 | ... | xk | | 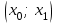 | 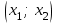 | ... | 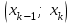 |
| n1 | n2 | ... | nk | | n1 | n2 | ... | nk |
| w1 | w2 | ... | wk | | w1 | w2 | ... | wk |
В случае непрерывного распределения величины X статистический ряд распределения представляет собой таблицу, в которой заданы интервалы значений величины X и соответствующие им частоты или относительные частоты, причем интервалы располагаются в порядке возрастания величины X (табл. 2).
Второй случай легко сводится к первому, если в качестве вариант брать середины интервалов:
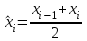
,
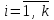 .
.-
Графическое изображение выборки
Графически табл. 1 изображается полигоном частот, представляющим собой ломаную, отрезки которой соединяют на плоскости соседние точки
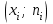 и
и 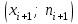 или
или 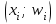 и
и 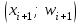 , если строится полигон относительных частот.
, если строится полигон относительных частот. В случае табл. 2 исходный интервал, в котором заключены все наблюдаемые значения признака, разбивают на определенное количество равных интервалов длины
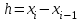 . После этого строится гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основания которых равны h, а высоты равны отношению
. После этого строится гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основания которых равны h, а высоты равны отношению 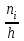 (или
(или 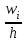 для гистограммы относительных частот).
для гистограммы относительных частот). Гистограмма относительных частот является аналогом функции плотности, так как площадь под ней равна единице. Число интервалов разбиения находят по формуле
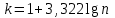 , где n – объем выборки. Тогда длина каждого интервала
, где n – объем выборки. Тогда длина каждого интервала 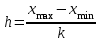 , где
, где 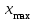 и
и 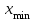 – максимальное и минимальное значение выборки соответственно.
– максимальное и минимальное значение выборки соответственно.-
Точечные оценки параметров распределения
По аналогии с такими числовыми характеристиками случайной величины, как математическое ожидание, дисперсия и среднее квадратическое отклонение, для выборки
 случайной величины X и для статистического ряда определяются следующие числовые характеристики:
случайной величины X и для статистического ряда определяются следующие числовые характеристики:выборочная средняя
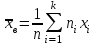 ,
,где k – число вариант и
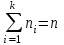
;
выборочная дисперсия
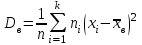
или
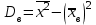 ,
, 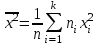 ;
;выборочное среднее квадратическое отклонение
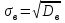
Во многих случаях бывает заранее известно, что функция распределения
 принадлежит к определенному классу функций распределения, зависящих от одного или нескольких параметров:
принадлежит к определенному классу функций распределения, зависящих от одного или нескольких параметров: 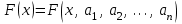 . В этом случае определение неизвестной функции распределения сводится к оценке неизвестных параметров по результатам выборки. Следует заметить, что ни при каких n нельзя определить по выборке точное значение неизвестного параметра, а можно найти его приближенное значение, которое называется оценкой по выборке неизвестного параметра. Всякая оценка по выборке является функцией
. В этом случае определение неизвестной функции распределения сводится к оценке неизвестных параметров по результатам выборки. Следует заметить, что ни при каких n нельзя определить по выборке точное значение неизвестного параметра, а можно найти его приближенное значение, которое называется оценкой по выборке неизвестного параметра. Всякая оценка по выборке является функцией 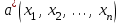 от выборочных значений
от выборочных значений  , так как она меняется от выборки к выборке. Функцию
, так как она меняется от выборки к выборке. Функцию 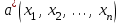 подбирают так, чтобы случайная величина
подбирают так, чтобы случайная величина 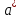 по возможности более точно аппроксимировала неслучайное неизвестное число a.
по возможности более точно аппроксимировала неслучайное неизвестное число a. Для выполнения данного условия накладывают следующие требования на оценку: несмещенность оценки, ее эффективность и состоятельность. Наиболее часто применяемыми метода получения оценок являются метод моментов и метод максимального правдоподобия.
Несмещенной и состоятельной оценкой математического ожидания
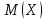 является выборочная средняя
является выборочная средняя 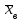 .
. Несмещенная и состоятельная оценка
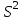 дисперсии
дисперсии 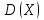 вычисляется по формуле:
вычисляется по формуле: