ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
гл = DfД/N, где D > 2 (D – де-фактор непосредственной связи с весовой функцией). Это приводит к увеличению числа каналов с перекрывающимися главными лепестками частотных характеристик и ухудшению разрешающей способности анализатора спектра.
Эксперимент 3:
Изучение обратного преобразования Фурье.
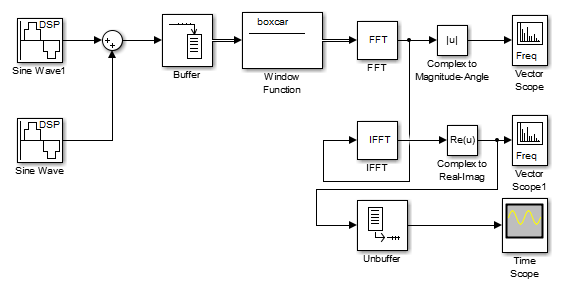
Рисунок 25 – Схема модели для задания 3
На рисунке 26 представлены спектрограммы и осциллограмма сигналов Прямоугольной функции после БПФ и ОБПФ при величине буфера 64.
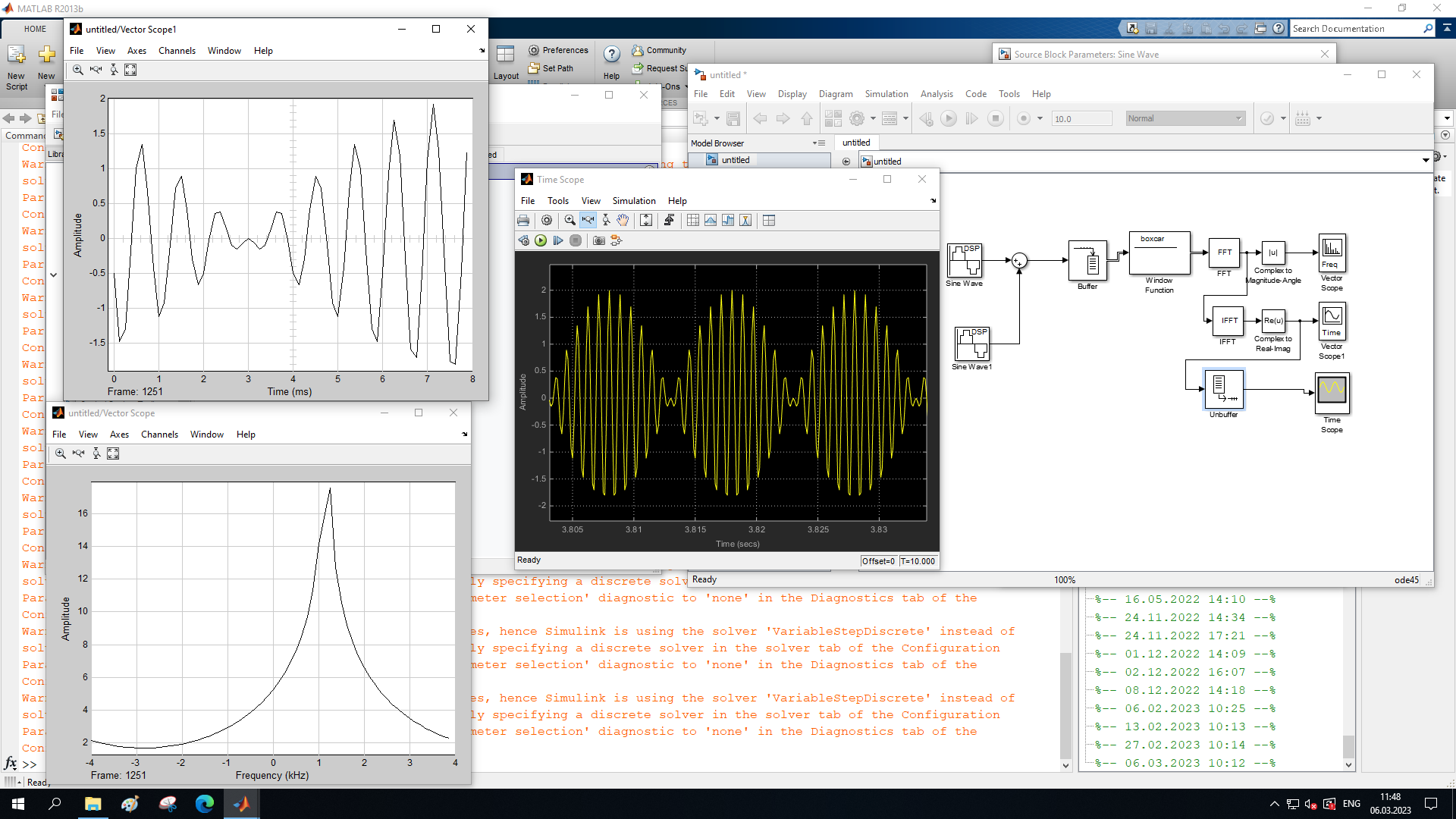
Рисунок 26 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно
На рисунке 27 представлены спектрограммы и осциллограмма сигналов функции Кайзера после БПФ и ОБПФ при величине буфера 64.
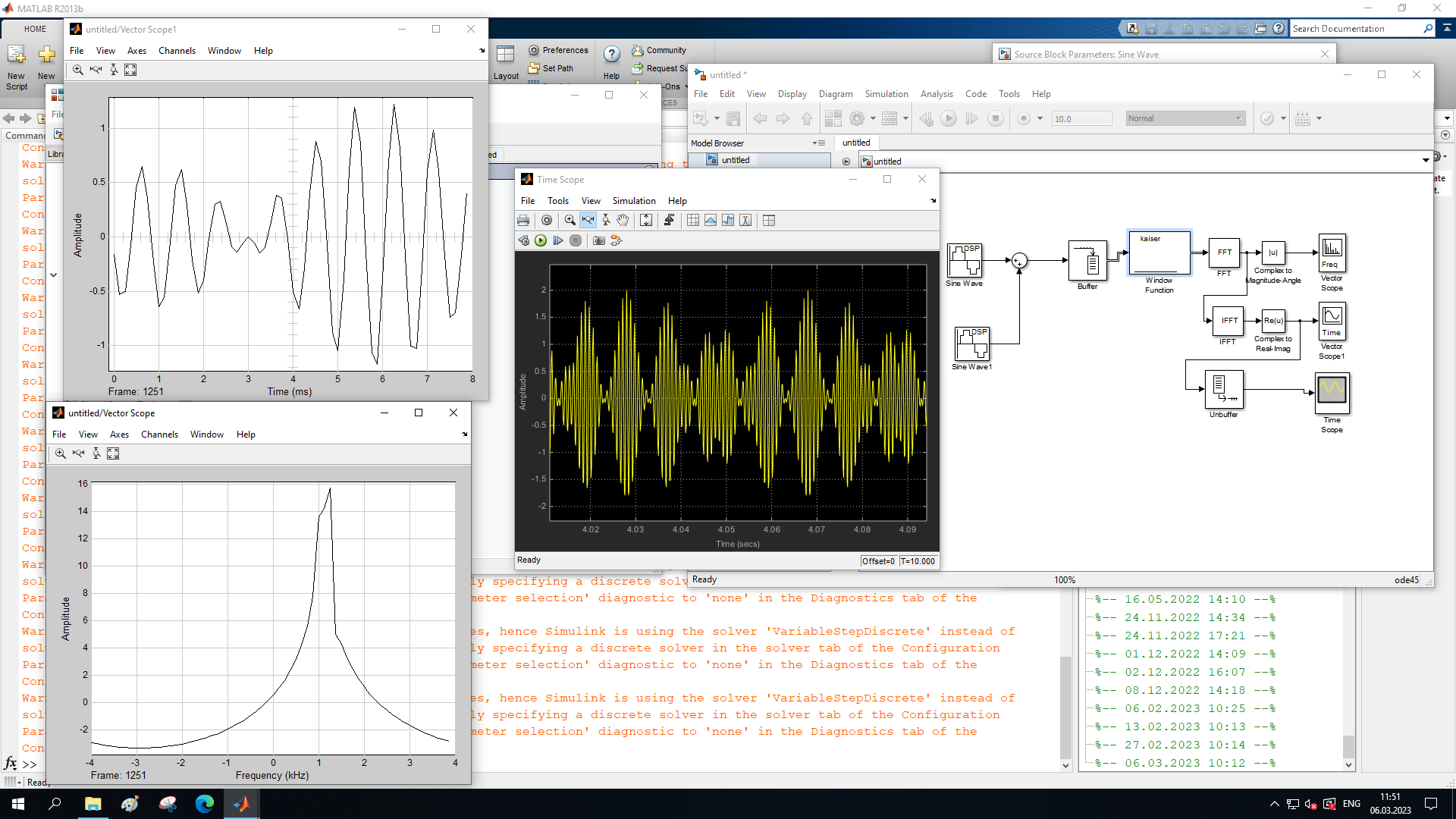
Рисунок 27 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно
На рисунке 28 представлены спектрограммы и осциллограмма сигналов функции Блэкмана после БПФ и ОБПФ при величине буфера 64.
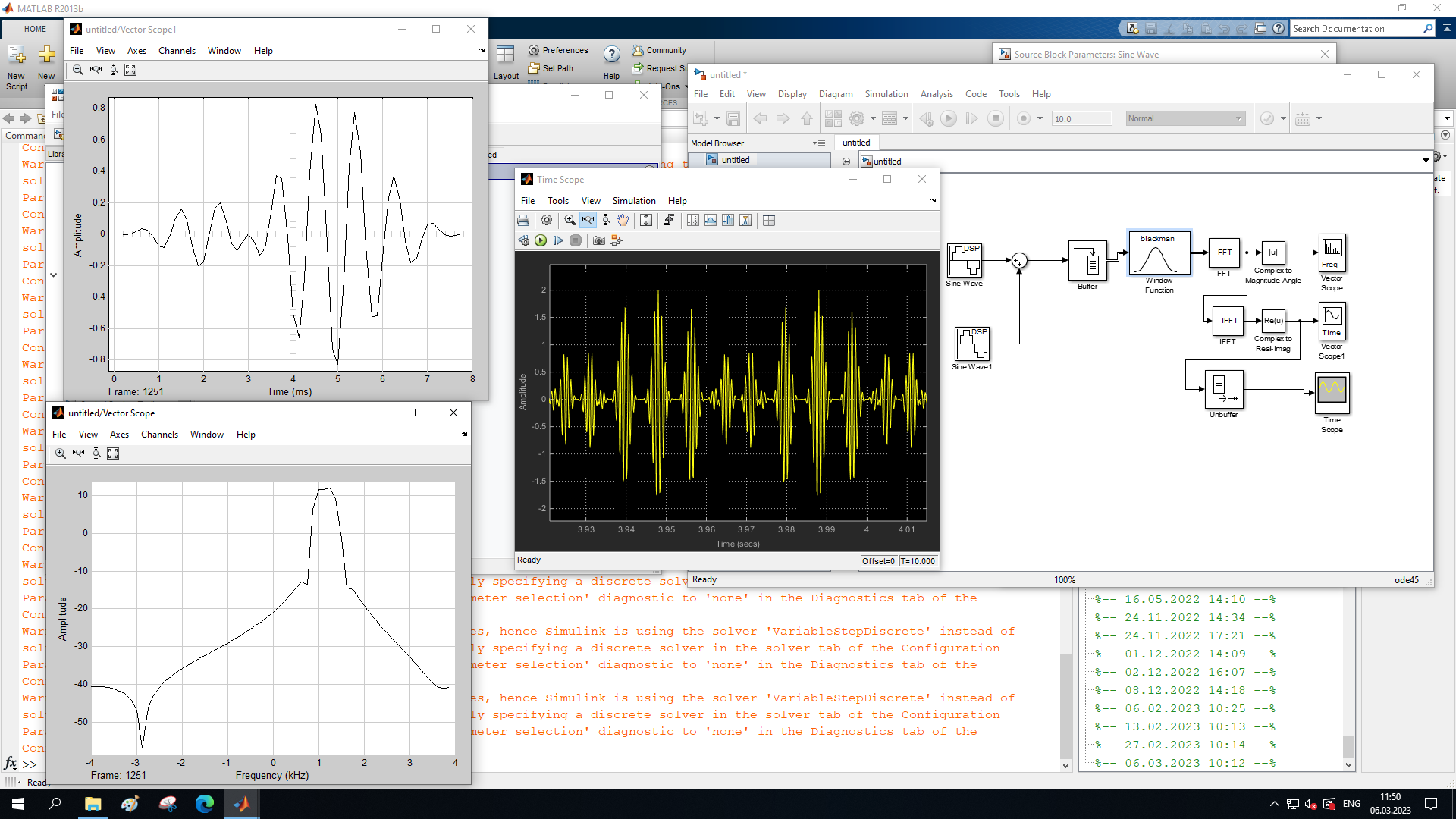
Рисунок 28 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно
Вывод: В ходе лабораторной работы изучены БПФ, эффекты просачивания и влияние весовых функций на просачивание, изучена разрешающая способность используемых весовых функций в зависимости от времени анализа, рассмотрена процедура обратного преобразования Фурье.
Контрольный вопрос:
3. Каковы основные параметры анализаторов спектра на основе ДПФ?
Анализатор спектра на основе ДПФ
В основе анализаторов спектра, использующих ДПФ, лежит базовая структура, приведенная на рис. 4. Она реализует базовые операции анализатора спектра – взвешивание и вычисление ДПФ. Ее выходом является вектор ДПФ входной в общем случае не ограниченной по длине последовательности x(n), усеченной весовой функцией w(n) конечной длины N:
k=0,1, …N–1.
Здесь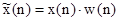
– преобразуемая входная последовательность ДПФ; ωk=k×ωд/N или fk=k×fд/N – частоты анализа, называемые также бинами ДПФ: 1 бин равен шагу дискретизации сигнала в частотной области fд/N. Анализатор имеет N разнесенных по частоте на 1 бин (fд/N) каналов анализа с центральными частотами ωk (fk), при этом значения k=0,1,…N–1 соответствуют номеру канала, номеру бина или номеру частотной выборки ДПФ 
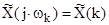. Весовая функция представляет окно, через которое наблюдается входной сигнал, длиной ее определяется время анализа Tа=N×Tд или время наблюдения сигнала.
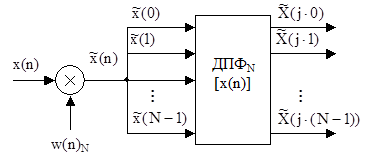
Рис. 4. Структурная схема анализатора спектра на основе ДПФ
Умножению или взвешиванию во временной области соответствует свертка в частотной, поэтому вычисляемое ДПФ фактически является дискретизированной сверткой истинного спектра анализируемого сигнала X(j×ω) с частотной характеристикой (спектром) весовой функции W(j×ω):
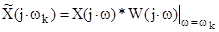, где * – символ свертки, т.е. содержит систематическую (методическую) погрешность анализа. Она является следствием ограничения сигнала по длительности, искажающего результаты спектрального анализа.
Эксперимент 3:
Изучение обратного преобразования Фурье.
-
Соберем схему, приведенную на рисунке 25. Схема по сравнению со схемами, используемыми в экспериментах 1 и 2 дополнительно содержит блоки обратного преобразования Фурье, преобразования комплексного сигнала в реальный и блока, преобразующего данные из массива в последовательные отсчеты. Зададим частоты генераторов 1100Гц и 1200Гц, амплитуду 1 вольт, частоту дискретизации 8кГц, весовую функцию прямоугольную, представления оси частот для векторного осциллографа (- fд/2 - fд/2), время моделирования 10 секунд.
Рисунок 25 – Схема модели для задания 3
На рисунке 26 представлены спектрограммы и осциллограмма сигналов Прямоугольной функции после БПФ и ОБПФ при величине буфера 64.
Рисунок 26 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно
-
Проводим моделирование данной схемы для функций Кайзера и Блэкмана.
На рисунке 27 представлены спектрограммы и осциллограмма сигналов функции Кайзера после БПФ и ОБПФ при величине буфера 64.
Рисунок 27 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно
На рисунке 28 представлены спектрограммы и осциллограмма сигналов функции Блэкмана после БПФ и ОБПФ при величине буфера 64.
Рисунок 28 – Спектрограмма сигнала после БПФ (левый), ОБПФ (правый) , осциллограмма (средний) соответственно
Вывод: В ходе лабораторной работы изучены БПФ, эффекты просачивания и влияние весовых функций на просачивание, изучена разрешающая способность используемых весовых функций в зависимости от времени анализа, рассмотрена процедура обратного преобразования Фурье.
Контрольный вопрос:
3. Каковы основные параметры анализаторов спектра на основе ДПФ?
Анализатор спектра на основе ДПФ
В основе анализаторов спектра, использующих ДПФ, лежит базовая структура, приведенная на рис. 4. Она реализует базовые операции анализатора спектра – взвешивание и вычисление ДПФ. Ее выходом является вектор ДПФ входной в общем случае не ограниченной по длине последовательности x(n), усеченной весовой функцией w(n) конечной длины N:
 , | (6) |
k=0,1, …N–1.
Здесь
– преобразуемая входная последовательность ДПФ; ωk=k×ωд/N или fk=k×fд/N – частоты анализа, называемые также бинами ДПФ: 1 бин равен шагу дискретизации сигнала в частотной области fд/N. Анализатор имеет N разнесенных по частоте на 1 бин (fд/N) каналов анализа с центральными частотами ωk (fk), при этом значения k=0,1,…N–1 соответствуют номеру канала, номеру бина или номеру частотной выборки ДПФ . Весовая функция представляет окно, через которое наблюдается входной сигнал, длиной ее определяется время анализа Tа=N×Tд или время наблюдения сигнала. 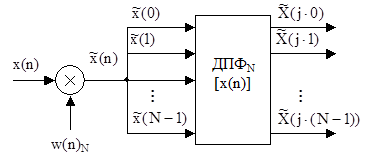Рис. 4. Структурная схема анализатора спектра на основе ДПФ
Умножению или взвешиванию во временной области соответствует свертка в частотной, поэтому вычисляемое ДПФ фактически является дискретизированной сверткой истинного спектра анализируемого сигнала X(j×ω) с частотной характеристикой (спектром) весовой функции W(j×ω):
, где * – символ свертки, т.е. содержит систематическую (методическую) погрешность анализа. Она является следствием ограничения сигнала по длительности, искажающего результаты спектрального анализа.