Файл: В. Ф. Пономарев математическая логика.doc

10) K₃={(АC); (BC); (АC); (BC); C; А; А ; B };

11) B(BC)=C – резольвента из 1) и 9);

12. 
    CA=(CA) – резольвента из 5) и 11);
    
13. 
    K₄={(АC); (BC); (АC); (BC); C; А; А; B; (CA)};
    
14. 
    (CA) (АC)=А – резольвента из 2) и 12);
    
15. 
    K₅={(АC); (BC); (АC); (BC); C; А; А; B; (CA)};
    
16. 
    АA= - пустая резольвента.
    

Так доказано, что если срабатывает клапан С, то не срабатывает клапан А.
Пример: Доказать истинность заключения

A ; В; (СAB)

С.

1) A - посылка;

2) B - посылка;

3) CA B = (CAB) - посылка;

4) (C) = C - отрицание заключения;

5) множество дизъюнктов: K={A; B; (CAB); C};

6) A(CAB)=(СB) - резольвента из 1) и 3);

7) K₁={A; B; (CAB); C; (СB)};

8) B(СB)=C - резольвента из 2) и 6);

9) K₂={A; B; (CAB); C; (СB); C };

10) СC = - пустая резольвента из 4) и 7).

Так доказана истинность заключения  C по принципу резолюции.
Пример: Доказать истинность заключения

( ABС ); (CD  M);( N DM )

ABN.
1) ABC=(AB)C=(ABC) - посылка;

2) CDM=(CD)M=(CDM) - посылка;

3)NDM=(N)DM=( N  D )( N  M ) - посылка;

4) ((AB)N)=ABN - отрицание заключения;

5. 
   множество дизъюнкций:
   

K={(ABC); (CDM); (ND); (NM); A; B;N};6) (MN)N=М - резольвента из 3) и 4);

7) K₁={(ABC); (CDM); (ND); (NM); A; B; M; N};

8) (DN)N=D - резольвента из 3) и 4);

9) K₂={(ABC); (CDM); (ND); (NM);A; B; M;N; D};

10) (ABC)B=(AC) – резольвента из 1) и 4);

11) K₃={(ABC); (CDM); (ND); (NM);A; B; M; N; D; (AC)};

12) (AC)A=C - резольвента из 4) и 10);

13) K₄={(ABC); (CDM); (ND); (NM);A; B; M; N; D; (AC); C};

14) (CDM)C =(DM) - резольвента из 2) и 12);

15) K₅={(ABC); (CDM); (ND); (NM);A; B; M; N; D; (AC); C; (DM)};

16) D(DM)=M - резольвента из 8) и 15;

17) K₆={(ABC); (CDM); (ND); (NM);A; B; M; N; D; (AC); C; (DM); M};

12) М M = - пустая резольвента.

Так доказана истинность заключения (ABN).

Для иллюстрации вывода удобно исполь­зовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а концевыми вершинами ветвей – оставшиеся дизъюнкты отрицания заключения и всех посылок. Узлами графа типа дерево являются резольвенты. Ниже даны примеры

---

, сопровождаемые графом.
Пример: Доказать истинность заключения

( AB)(CD); (DBM); M

(AC)

1) (AB)(CD)=(AB)(CD) - посылка;

2) DBM=(DB)M=(DBM) - посылка;

3)  M - посылка;

4) (  A  C ) = A  C - отрицание заключения;

5) K ={A; C; M; (AB); (CD); (DBM)}

6) A(AB)=B - резольвента;

7) B(DBM)=(DM) - резольвента;

8) (DM)(CD)=(CM) - резольвента;

9) (CM)M=C - резольвента;

10)CC= - пустая резольвента.

Так доказана истинность заключения (AC).


A






(AB)


B


(DBM)
(DM)

(CD)
(CM)


M

C


C


Рис.6. Граф доказательства
Пример: Доказать истинность заключения

( ( AB)C); (С(DB)); (СN); ((D)( N))

 A.

1) ((AB)C)=(AC)(BC) - посылка;

2) (C(DB))=(BCD) - посылка;

3) (CN) = (CN) - посылка;

4)D - посылка;

5) N - посылка;

6) (A)=A – отрицание заключения;

7) K={(AC); (BC); (BCD); (CN);D;N; A};

8)
A

(AC)
A(AC)=C – резольвента из 1) и 6);

9) C(BCD)=(BD) – резольвента из 2) и 7);

10) (BD)(BC)=(CD) – резольвента из 1) и 8);

11) (CD)D=C – резольвента из 4) и 9);

12) C(CN)=N – резольвента из 3) и 10);

1
Следует обратить внимание, что при выводе заключения дважды получена резольвента С. Это говорит об избыточности посылок. Например, можно удалить (C(DB)), формирующую дизъюнкт (BCD). Это существенно сократит вывод заключения. На рис. 8 показан вывод заключения без учета посылки (C(DB)).

3) NN= - пустая резольвента.

A

C

---

(AC)


C


(BCD)

(BD)

(BC)

(CD)

D

C

(CN)

N

N
N




Рис. 7. Граф доказательства.
1
A
) A(AC)=C – резольвента из 1) и 6);

2
(AC)

С
) C(CN)=N – резольвента из 3) и 14);


(CN)

N

3) NN= - пустая резольвента.


N

N





Рис. 8 Граф доказательства
Так как резольвенты включаются в множество дизъюнктов S, то возможно неоднократное их использование в процессе вывода. Многократное использование дизъюнкт множества S оправдано законом идемпотентности, т.к. D_i=D_iD_i...D_i.

Пример: Доказать истинность заключения

(AB); (AB);

(AB).

1) (AB) - посылка;

2) (AB)=(AB)(BA) - посылка;

3 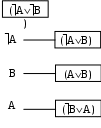)(AB)=(AB) –отрицание заключения;

4 ) K = {(AB); (AB); (BA); (AB)};

5) (AB)(AB)= A - резольвента;

6) A(AB)=B - резольвента;

7) B(BA)=A - резольвента;

8) AA=  - пустая резольвента.


A


Р ис. 9 Граф доказательства 
Достоинством принципа резолюции является то, что при доказательстве истинности заключения применяют только одно правило: поиск и удаление контрарных литер на множестве дизъюнктов до получения пустой резольвенты.

5. 
   Проблемы в исчислении высказываний
   

Для обоснования исчисления высказываний, как для любой аксиоматической теории, необходимо рассмотреть проблемы разрешимости и непротиворечивости.

Проблема разрешимости исчисления выказываний заключена в доказательстве существования алгоритма, который позволил бы для любой формулы исчисления высказываний определить ее доказуемость. Любая формула исчисления высказываний может быть представлена формулой алгебры высказываний. Эффективность процедуры разрешения показана таблицами истинности для различных наборов значений пропозициональных переменных.

---

Проблема непротиворечивости исчисления высказываний заключена в доказательстве невыводимости формулы и ее отрицания.

Исчисление высказываний непротиворечиво, т. к. каждая формула, доказуемая в исчислении высказываний, является тождественно истинной формулой в алгебре высказываний и легко проверяется на таблицах истинности. Тогда отрицание формулы не является тождественно истинной формулой, что проверяется на таблицах истинности и при доказательстве в исчислении высказываний ведет к противоречию.

1.6 Описание высказываний на языке PROLOG

Для программирования задач исчисления высказываний используют язык программирования Prolog.Само название Prolog есть сокращение, означающее программирование в терминах логики.

Пролог-программа состоит из предложений, которые бывают трех типов: факты, правила и вопросы.

Факты есть высказывания, которые заканчиваются точкой и имеют значение только “и”. Структура такого предложения описана предикатом или n-местным отношением, все аргументы которого есть термы или предметные постоянные. Предметные постоянные на языке PROLOG называют атомами. Термы описывают структуру или какие-то функциональные отношения между атомами. Предметные постоянные всегда начинаются со сточной буквы латинского алфавита и представляют собой последовательность букв, цифр и знака подчеркивания.

Например,

• 
  простое_число(3).
  

Это есть высказывание A1 (см. с. 5), структура которого описана предикатом P1(x):=”x-простое число”, где x=3 есть атом.

• 
  частное_от_деления(6, 2, 3).
  

Это есть высказывание Е (см. с.6), структура которого описана предикатом P₃(x, y, z):=”z есть частное от деления числа x на y”, где x=6, y=2, z=3 есть атомы.

• 
  студент_университета,_обучающийся_по_специальности(Петров, КГТУ, прикладная информатика").
  

Это есть высказывание, структура которого описана предикатом

P₆(x, y, z):= "студент x университета y, обучающийся по специальности z”, где x=”Петров”, y=”КГТУ”, z=”прикладная информатика” есть атомы.

• 
  родословная русских князей X века:
  

отец(игорь, святослав).

отец(святослав,владимир).

отец(владимир, борис).

отец(владимир,глеб).

---

дед(игорь, владимир).

дед(святослав, борис).

дед(святослав, глеб).

брат(борис,глеб).,
где игорь, святослав, владимир, борис, глеб есть атомы.Правила есть предложения, истинность которых зависит от истинности условий: “если истинны условия (посылки), то истинно и заключение (вывод)”.

На языке Prolog эти правила записывают так:

<заключение>:- <условия>.

Символ “:-“ соответствует символу обратной импликации ””.

Левую часть правила называют головой предложения, а правую – телом предложения. В теле предложения перечисляют условия, определяющие вывод заключения. Если условия имеют между собой конъюнктивную связь, то между ними ставится запятая “,”. Если условия в правиле имеют между собой дизъюнктивную связь, то между ними ставится точка с запятой (“;”). Голова предложения всегда сдвинута влево относительно перечня условий. Каждое условие начинается с новой строки.

Например, для родословной русских князей X века имеем:

• 
  дед(игорь, владимир):-
  

отец(игорь, святослав),

отец(святослав, владимир).

Это - высказывание о том, что если игорь был отцом святослава, а святослав – отцом владимира, то игорь был дедом владимиру.

• 
  дед(святослав, борис); дед(святослав, глеб):-отец(святослав,владимир),
  

отец(владимир, борис);

отец(святослав,владимир),

отец(владимир,глеб).

Это есть высказывание о том, что святослав был отцом владимира и дедом борису или глебу.

• 
  брат(борис, глеб):-.
  

родитель (владимир, борис),

родитель (владимир,глеб).

Это есть высказывание о том, что если владимир был отцом бориса и отцом глеба, то борис и глеб были братьями
.


Контрольные вопросы

1) Запишите символически следующие суждения:

а) “вертолет является средством передвижения по воздуху, имеет двигатель, пилотскую кабину, систему управления, несущий винт, по­мещение для пассажиров или грузов”;

б) “подготовка специалистов высокой квалификации возможна лишь на базе всемерного развития вузовской науки, усиления связи вузов­ской, академической и отраслевой науки, обеспечения единства науч­ной и учебной работы, широкого привлечения студентов к научным ис­следованиям" ;

в) "хлеба уцелеют в различных климатических и погодных усло -виях тогда и только тогда, когда будут выполнены все мелиоративные работы; если хлеба не уцелеют, то фермеры обанкротятся и оставят фермы; следовательно, необходимо выполнить все мелиоративные работы"[15].

---