ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 324
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=(AA’)(BB’) - посылка;
2) F2=(AA’) - заключение по формуле F1 и правилу удаления логической связки конъюнкции;
3) F3=(BB’) - заключение по формуле F1 и правилу удаления логической связки конъюнкции;
4) F4=(AB’)(BA’) - посылка;
5) F5=(AB’) - заключение по формуле F4 и правилу удаления логической связки конъюнкции;
6) F6=(BA’) - заключение по формуле F4 и правилу удаления логической связки конъюнкции;
7) F7=(B’A) - заключение по формуле F5 и закону контрапозиции;
8) F8=(A’B) - заключение по формуле F6 и закону контрапозиции;
9) F9=(AB) - посылка;
10) F10=AB - заключение по формуле F9 и правилу эквивалентного преобразования;
11) F11=AA’ - заключение по формулам F6, F10 и закону силлогизма;
12) F12= B’A’ - заключение по формулам F7, F11 и закону силлогизма;
13) F13= A’A - заключение по формуле F2 и закону контрапозиции;
14) F14=A’B - заключение по формулам F10, F13 и закону силлогизма;
15) F15=A’B’ - заключение по формулам F3, F14 и закону силлогизма;
16) F16= (B’A’)(A’B’)=(B’A’) – заключение по формулам F12, F15 и правилу введения логической связки конъюнкции.
Так доказана истинность формулы (B’A’).
Пример. "Если Петров говорит неправду (A), то он заблуждается (В) или сознательно вводит в заблуждение других (С). Петров говорит неправду и явно не заблуждается. Следовательно, он сознательно вводит в заблуждение других" [2]
 А(ВС); AB
А(ВС); AB
С.
1) F1=А(ВС) - посылка;
2) F2=AB - посылка;
Так доказано, что Петров сознательно вводит в заблуждение других.
П ример: Доказать истинность заключения
ример: Доказать истинность заключения
А;В;(АС В)
C. 1) F1=A C B - посылка;2) F2=B - посылка;
3) F3= ( A C ) - заключение по формулам F1, F2 и правилу m. t.;
4) F4= A - посылка;
5) F5= C - заключение по формула F3, F4 и правилу 2).
Процесс дедуктивного вывода удобно проследить на графе, вершинами которого являются формулы, а дугами – отношения между ними (см. рис.1).
A
(AC)

Рис.1. Граф вывода заключения
Пример. Доказать истинность заключения
(AB); (AC); (BD)
 (CD).
(CD).
1) F1=(AC) посылка;
3) F3=(BD) посылка;
4) F4=(CB)(CD) заключение по формуле F3 и правилу 9);
5) F5=(AB)(CD) заключение по формулам F2 и F4 и правилу 11);
6) F6=(AВ) посылка;
7) F7=(CD) заключение по формулам F5 и F6 и правилу m. p..
Так доказана истинность заключения (CD).
AC
BD
AВ

(AB)(CB)
(CB)(CD)


(AB)(CD)
CD
Рис. 2. Граф вывода заключения
Пример: Доказать истинность заключения
(AB)(CD); ( DBE ); E
 C A.
C A.
1) F1=(DBE) посылка;
2) F2=E посылка;
3) F3=(DB) заключение по формулам F1 и F2 и правилу m. t.;
4) F4=(АВ)(СD) посылка;
5) F5=(AВ) заключение по формуле F4 и правилу 2);
6) F6=(СD) заключение по формуле F4 и правилу 2);
7) F7=(BA) заключение по формуле F5 и правилу 8);
8) F8=(DB) заключение по формуле F3 и закону де Моргана;
9) F9=(DB) заключение по формуле 8) и правилу введения ипликации;
10) F10=(D A) заключение по формулам F7 и F9 и правилу 11);
11) F11=(С A) заключение по формулам F6 и F10 и правилу 11);
12) F12=(С A) заключение по формуле FII и правилу введения дизъюнкции.
(АВ)(СD)
(DBE)
E


(AВ)
(СD)
(DB)
(DB)
(BA)
(D A)
(DB)

Рис.3. Граф вывода заключения
(С A)
(С A)

Пример: Доказать истинность заключения :
 ((A B) С); (С(D M )); (MN); (( D)( N))
((A B) С); (С(D M )); (MN); (( D)( N))
A.
1) F1=(( D)( N)) посылка;
2) F2=N заключение по формуле F1 и правилу 2);
3) F3=(MN); посылка ;
4) F4=M заключение по формулам F2 и F3 и правилу m.t;
5) F5=D заключение по формуле F1 и правилу 2);
6) F6=(D)(M) заключение по формулам F
4 и F5 и правилу 1);
7) F7=(DМ) заключение по формуле F6 и закону де Моргана;
8) F8=(( AB)C) посылка;
9) F9=(С (DМ)) посылка;
10) F10=((AB)(DM)) заключение по формулам F8 и F9 и правилу 11);
11) F11=(AB) заключение по формулам F7 и F10 и правилу m.t.;
12) F12=(А)(B) заключение по формуле F11 и закону де Моргана;
13) F13=A заключение по формуле F12 и правилу 2).
((D)(N))
(MN)
(( AB)C)
(С(DМ))



(D)
(N)
(M)
( AB)(DМ)

(D)(M)
(DМ)
(AB)


(А)(B)
A
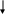

Рис. 4. Граф вывода заключения
Эти примеры показывают, что правила вывода обеспечивают логическую последовательность в преобразовании формул, каждая из которых есть либо посылка, либо промежуточный результат, либо заключение.
Существует эффективный алгоритм логического вывода - алгоритм резолюции. Этот алгоритм основан на том, что выводимость формулы В из множества посылок F1; F2; F3; . . . Fn равносильна доказательству теоремы
(F1F2F3. . .FnB),
формулу которой можно преобразовать так:
(F1F2F3. . .FnB) =
((F1F2F3. . .Fn)B) =
(F1F2F3. . .Fn( F2 B)).
Следовательно, заключение В истинно тогда и только тогда, когда формула (F1F2F3...Fn(B))=л. Это возможно при значении “л” хотя бы одной из подформул Fi илиB.
Для анализа этой формулы все подформулы Fi иB должны быть приведены в конъюнктивную нормальную форму и сформировано множество дизъюнктов, на которые распадаются все подформулы. Два дизъюнкта этого множества, содержащие пропозициональные переменные с противоположными знаками (контрарные атомы) формируют третий дизъюнкт - резольвенту, в которой будут исключены контрарные пропозициональные переменные. Неоднократно применяя это правило к множеству дизъюнктов и резольвент, стремятся получить пустой дизъюнкт. Наличие пустого дизъюнкта свидетельствует о выполнении условия F1F2F3...FnB=л.
1.4.1 Алгоритм вывода по принципу
резолюции
Шаг 1. принять отрицание заключения, т.е. В;
Шаг 2. привести все формулы посылок и отрицания заключения к конъюнктивной нормальной форме (см. с.35);
Шаг 3. выписать множество дизъюнктов всех посылок и отрицания заключения:
K = {D1; D2; . . . Dk };
Шаг 4. выполнить анализ пар множества K по правилу:
“если существуют дизъюнкты Di и Dj, один из которых (Di) содержит литеру А, а другой (Dj) - контрарную литеру А, то соединить эту пару логической связкой дизъюнкции (Di Dj) и сформировать новый дизъюнкт - резольвенту, исключив контрарные литеры А и А;
Шаг5. если в результате соединения дизъюнктов, содержащих контрарные литеры, будет получена пустая резольвента - , то конец (доказательство подтвердило противоречие), в противном случае включить резольвенту в множество дизъюнктов K и перейти к шагу 4.
Пример: Работа автоматического устройства, имеющего три клапана А, В и С, удовлетворяет следующим условиям: если не срабатывают клапаны А или В или оба вместе, то срабатывает клапан С; если срабатывают клапаны А или В или оба вместе, то не срабатывает клапан С. Следовательно, если срабатывает клапан С, то не срабатывает клапан А [2].
((АBА B)С); ((ABАB)C)
 (CA).
(CA).
1) F1=((АBА B)С)= (АC)(BC) - посылка;
2) F2=((ABАB)C)= (АC)(BC) -посылка;
3) F3= (CA)=CА –отрицание заключения;
2) F2=(AA’) - заключение по формуле F1 и правилу удаления логической связки конъюнкции;
3) F3=(BB’) - заключение по формуле F1 и правилу удаления логической связки конъюнкции;
4) F4=(AB’)(BA’) - посылка;
5) F5=(AB’) - заключение по формуле F4 и правилу удаления логической связки конъюнкции;
6) F6=(BA’) - заключение по формуле F4 и правилу удаления логической связки конъюнкции;
7) F7=(B’A) - заключение по формуле F5 и закону контрапозиции;
8) F8=(A’B) - заключение по формуле F6 и закону контрапозиции;
9) F9=(AB) - посылка;
10) F10=AB - заключение по формуле F9 и правилу эквивалентного преобразования;
11) F11=AA’ - заключение по формулам F6, F10 и закону силлогизма;
12) F12= B’A’ - заключение по формулам F7, F11 и закону силлогизма;
13) F13= A’A - заключение по формуле F2 и закону контрапозиции;
14) F14=A’B - заключение по формулам F10, F13 и закону силлогизма;
15) F15=A’B’ - заключение по формулам F3, F14 и закону силлогизма;
16) F16= (B’A’)(A’B’)=(B’A’) – заключение по формулам F12, F15 и правилу введения логической связки конъюнкции.
Так доказана истинность формулы (B’A’).
Пример. "Если Петров говорит неправду (A), то он заблуждается (В) или сознательно вводит в заблуждение других (С). Петров говорит неправду и явно не заблуждается. Следовательно, он сознательно вводит в заблуждение других" [2]
 А(ВС); AB
А(ВС); ABС.
1) F1=А(ВС) - посылка;
2) F2=AB - посылка;
3) F3=A - заключение по формуле F2 и правилу 2);
4) F4=B - заключение по формуле F2 и правилу 2);
5) F5=(ВС) - заключение по формулам F1, F3 и правилу m. p.;
6) F6=C - заключение по формулам F4, F5 и правилу 5).
Так доказано, что Петров сознательно вводит в заблуждение других.
П
 ример: Доказать истинность заключения
ример: Доказать истинность заключенияА;В;(АС В)
C. 1) F1=A C B - посылка;2) F2=B - посылка;
3) F3= ( A C ) - заключение по формулам F1, F2 и правилу m. t.;
4) F4= A - посылка;
5) F5= C - заключение по формула F3, F4 и правилу 2).
Процесс дедуктивного вывода удобно проследить на графе, вершинами которого являются формулы, а дугами – отношения между ними (см. рис.1).
B
ACB
A
(AC)
C

Рис.1. Граф вывода заключения
Пример. Доказать истинность заключения
(AB); (AC); (BD)
 (CD).
(CD).1) F1=(AC) посылка;
-
F2=(AB)(CB) заключение по формуле F1 и правилу 9);
3) F3=(BD) посылка;
4) F4=(CB)(CD) заключение по формуле F3 и правилу 9);
5) F5=(AB)(CD) заключение по формулам F2 и F4 и правилу 11);
6) F6=(AВ) посылка;
7) F7=(CD) заключение по формулам F5 и F6 и правилу m. p..
Так доказана истинность заключения (CD).
AC
BD
AВ

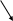
(AB)(CB)
(CB)(CD)


(AB)(CD)
CD
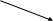
Рис. 2. Граф вывода заключения
Пример: Доказать истинность заключения
(AB)(CD); ( DBE ); E
 C A.
C A.1) F1=(DBE) посылка;
2) F2=E посылка;
3) F3=(DB) заключение по формулам F1 и F2 и правилу m. t.;
4) F4=(АВ)(СD) посылка;
5) F5=(AВ) заключение по формуле F4 и правилу 2);
6) F6=(СD) заключение по формуле F4 и правилу 2);
7) F7=(BA) заключение по формуле F5 и правилу 8);
8) F8=(DB) заключение по формуле F3 и закону де Моргана;
9) F9=(DB) заключение по формуле 8) и правилу введения ипликации;
10) F10=(D A) заключение по формулам F7 и F9 и правилу 11);
11) F11=(С A) заключение по формулам F6 и F10 и правилу 11);
12) F12=(С A) заключение по формуле FII и правилу введения дизъюнкции.
(АВ)(СD)
(DBE)
E

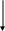

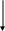
(AВ)
(СD)
(DB)
(DB)
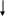
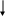
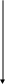
(BA)
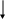
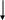
(D A)
(DB)

Рис.3. Граф вывода заключения
(С A)
(С A)

Пример: Доказать истинность заключения :
 ((A B) С); (С(D M )); (MN); (( D)( N))
((A B) С); (С(D M )); (MN); (( D)( N)) A.
1) F1=(( D)( N)) посылка;
2) F2=N заключение по формуле F1 и правилу 2);
3) F3=(MN); посылка ;
4) F4=M заключение по формулам F2 и F3 и правилу m.t;
5) F5=D заключение по формуле F1 и правилу 2);
6) F6=(D)(M) заключение по формулам F
4 и F5 и правилу 1);
7) F7=(DМ) заключение по формуле F6 и закону де Моргана;
8) F8=(( AB)C) посылка;
9) F9=(С (DМ)) посылка;
10) F10=((AB)(DM)) заключение по формулам F8 и F9 и правилу 11);
11) F11=(AB) заключение по формулам F7 и F10 и правилу m.t.;
12) F12=(А)(B) заключение по формуле F11 и закону де Моргана;
13) F13=A заключение по формуле F12 и правилу 2).
((D)(N))
(MN)
(( AB)C)
(С(DМ))



(D)
(N)
(M)
( AB)(DМ)

(D)(M)
(DМ)
(AB)


(А)(B)
A
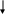

Рис. 4. Граф вывода заключения
Эти примеры показывают, что правила вывода обеспечивают логическую последовательность в преобразовании формул, каждая из которых есть либо посылка, либо промежуточный результат, либо заключение.
-
Принцип резолюции
Существует эффективный алгоритм логического вывода - алгоритм резолюции. Этот алгоритм основан на том, что выводимость формулы В из множества посылок F1; F2; F3; . . . Fn равносильна доказательству теоремы
(F1F2F3. . .FnB),
формулу которой можно преобразовать так:
(F1F2F3. . .FnB) =
((F1F2F3. . .Fn)B) =
(F1F2F3. . .Fn( F2 B)).
Следовательно, заключение В истинно тогда и только тогда, когда формула (F1F2F3...Fn(B))=л. Это возможно при значении “л” хотя бы одной из подформул Fi илиB.
Для анализа этой формулы все подформулы Fi иB должны быть приведены в конъюнктивную нормальную форму и сформировано множество дизъюнктов, на которые распадаются все подформулы. Два дизъюнкта этого множества, содержащие пропозициональные переменные с противоположными знаками (контрарные атомы) формируют третий дизъюнкт - резольвенту, в которой будут исключены контрарные пропозициональные переменные. Неоднократно применяя это правило к множеству дизъюнктов и резольвент, стремятся получить пустой дизъюнкт. Наличие пустого дизъюнкта свидетельствует о выполнении условия F1F2F3...FnB=л.
1.4.1 Алгоритм вывода по принципу
резолюции
Шаг 1. принять отрицание заключения, т.е. В;
Шаг 2. привести все формулы посылок и отрицания заключения к конъюнктивной нормальной форме (см. с.35);
Шаг 3. выписать множество дизъюнктов всех посылок и отрицания заключения:
K = {D1; D2; . . . Dk };
Шаг 4. выполнить анализ пар множества K по правилу:
“если существуют дизъюнкты Di и Dj, один из которых (Di) содержит литеру А, а другой (Dj) - контрарную литеру А, то соединить эту пару логической связкой дизъюнкции (Di Dj) и сформировать новый дизъюнкт - резольвенту, исключив контрарные литеры А и А;
Шаг5. если в результате соединения дизъюнктов, содержащих контрарные литеры, будет получена пустая резольвента - , то конец (доказательство подтвердило противоречие), в противном случае включить резольвенту в множество дизъюнктов K и перейти к шагу 4.
Пример: Работа автоматического устройства, имеющего три клапана А, В и С, удовлетворяет следующим условиям: если не срабатывают клапаны А или В или оба вместе, то срабатывает клапан С; если срабатывают клапаны А или В или оба вместе, то не срабатывает клапан С. Следовательно, если срабатывает клапан С, то не срабатывает клапан А [2].
((АBА B)С); ((ABАB)C)
 (CA).
(CA).1) F1=((АBА B)С)= (АC)(BC) - посылка;
2) F2=((ABАB)C)= (АC)(BC) -посылка;
3) F3= (CA)=CА –отрицание заключения;
-
множество дизъюнктов: K={(АC); (BC); (АC); (BC); C; А }; -
С(АC)=А – резольвента из 2) и 3); -
K1={(АC); (BC); (АC); (BC); C; А; А }; -
А(АC)=C – резольвента из 1) и 5); -
K2={(АC); (BC); (АC); (BC); C; А; А }; -
С(BC)=B –резольвента из 2) и 5);