ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТАФедеральное государственное бюджетное образовательное учреждениевысшего образования«Петербургский государственный университет путей сообщения Императора Александра I»(ФГБОУ ВО ПГУПС)–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– Факультет «Безотрывных форм обучения» Специальность  «Подвижной состав железных дорог» Специализация ”Электрический транспорт”  ЛАБОРАТОРНАЯ РАБОТА №1по дисциплине«Теория и конструкция локомотивов»На тему: «Анализ характеристик листовой рессоры локомотива»Вариант №5Форма обучения – заочная  Выполнил обучающийсяКурс 4Группа ЭТ-921з. Трофимов Ю.С.^{__________________________________________________подпись, дата}Руководитель. Кручек В.А.^{__________________________________________________ подпись, дата}Санкт-Петербург2022г.Целью лабораторной работы является расчёт упругодиссипативных свойств и прочности листовых рессор, применяемых в рессорном подвешивании тягового подвижного состава.Исходные данные:Р_ст = 112 кН, L₀= 119 см, f_c= 7,8 см, y_a = 3,4 см, b = 12 см, h = 1,6 смРасчет листовой рессоры рессорного подвешивания тепловоза:

1. 
   Расчёт параметров рессоры.
   

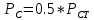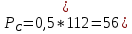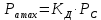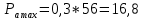Расчетная статическая нагрузка на половину рессоры, кН: (1.1) кН)Максимальная динамическая составляющая нагрузки, кН: (1.2) (кН)Расстояние от плоскости середины хомута до точки приложения нагрузки, см:

---

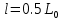
(1.3)



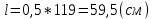
Максимальная расчетная нагрузка на половину рессоры, кН:

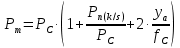, (1.4)

где .

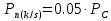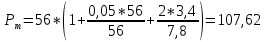(кН)

Пробная нагрузка, кН:

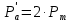(1.5)

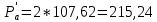(кН)

Момент сопротивления сечения листа, см³:

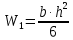(1.6)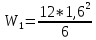

= 5,12 (см²)

Допускаемая величина максимальных рабочих напряжений в листах рессоры, МПа:

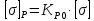, (1.7)

где 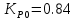– коэффициент снижения уровня максимальных рабочих напряжений.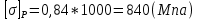



Количество листов:

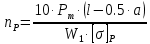(1.8)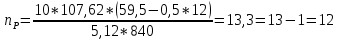

(листов)

Количество листов принимается с округлением в меньшую сторону и дополнительным вычитанием одного листа.

Общее количество листов разбивается на количество коренных листов m и количество ступенчатых рессор n. При определении количества коренных листов необходимо придерживаться следующего правила: если общее количество листов рессор меньше восьми включительно, брать два коренных листа; в других случаях – три.

m = 3, n = 9

Шаг удлинения листов, см:

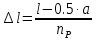(1.9)

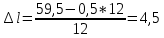(см)

Полученный шаг удлинения листов округляется с шагом 0,5 см. Например, если получилось 4,9 см, то округлить до 5,0 см, если получилось 5,7 см, то округлить до 5,5 см.

Длина первого ступенчатого листа (самого длинного), см:

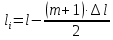(1.10)

где i = m+1 – номер первого ступенчатого листа.

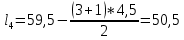(см)

Полученную длину первого ступенчатого листа округляем в меньшую сторону до целого значения.

---

Длины остальных листов ступенчатой части, см: 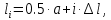(1.11)где i – шаг расчёта ступенчатого листа, i = n–m–1…1 (с шагом минус 1). 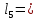0,5 * 12 + 8 * 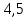= 42 (см) 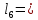0,5 * 12 + 7 * 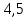= 37,5 (см) 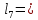0,5 * 12 + 6 * 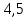= 33 (см) 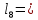0,5 * 12 + 5 * 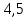= 28,5 (см) 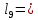0,5 * 12 + 4* 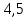= 24 (см) 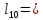0,5 * 12 + 3 * 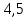= 19,5(см) 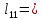0,5 * 12 + 2 * 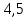= 15 (см) 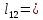0,5 * 12 + 1 * 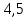= 10,5 (см)Момент инерции сечения листа, см⁴: 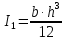(1.12) 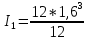= 4,1 (см⁴)Действительный статический прогиб без учета сил трения, см: 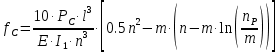, (1.12)где ln – натуральный логарифм. 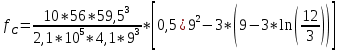= 4,88 (см)Коэффициент динамичности прогибов: 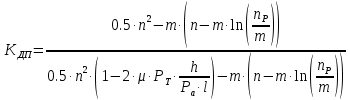(1.13)Результаты расчёта величин К_ДП для различных значений μ и Р_Т/Р_а сводим в таблицу 1.Коэффициент динамичности прогибов для μ=0,4, P_Т/P_a = 1: 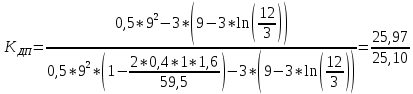= 1,03Коэффициент динамичности напряжений:

---

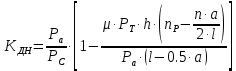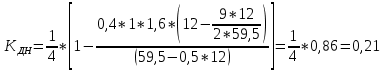
(1.14)Результаты расчёта величин К_ДН для различных значений μ, Р_Т/Р_а и Р_С/Р_а сводим в таблицу 1.Коэффициент динамичности напряжений при μ = 0,4 и P_c/P_a = 1:Таблица 1. Коэффициенты динамичности.Результаты расчёта величин 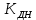для различных значени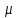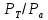й , и 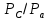сводим в таблицу 1.Таблица 1. Коэффициенты динамичности

Коэффициенты динамичности	µ	Отношение ,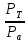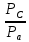
		9	8	6	4	2	1
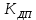	0,1	1,08	1,07	1,05	1,03	1,01	1,008
	0,2	1,17	1,15	1,11	1,07	1,03	1,01
	0,3	1,29	1,25	1,17	1,11	1,05	1,02
	0,4	1,43	1,36	1,25	1,15	1,07	1,03
	0,5	1,6	1,5	1,33	1,19	1,09	1,04
	0,6	1,82	1,67	1,43	1,23	1,11	1,05
	0,7	2,11	1,88	1,54	1,27	1,13	1,06
	0,8	2,52	2,15	1,67	1,31	1,15	1,07
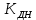	0,1	0,07	0,09	0,13	0,21	0,46	0,96
	0,2	0,04	0,05	0,1	0,18	0,43	0,93
	0,3	0,01	0,25	0,06	0,15	0,4	0,9
	0,4	-0,02	-0,007	0,03	0,11	0,36	0,86
	0,5	-0,05	-0,04	0,00	0,08	0,33	0,83
	0,6	-0,08	-0,07	-0,03	0,05	0,3	0,8
	0,7	-0,12	-0,1	-0,06	0,01	0,26	0,76
	0,8	-0,15	-0,14	-0,09	-0,01	0,23	0,73

---

Диапазон разброса статического прогиба при учете сил трения, см: 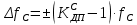(1.15) 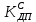принимается по табл. 1 при μ = 0,4 и P_Т/P_a = 1. 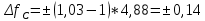(см)Расчётный чертежный статический прогиб, см: 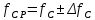(1.16) 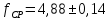(см)Статическая жесткость рессоры, кН/см: 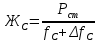(1.17) 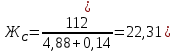кН/см)Динамическая жесткость пружины, кН/см: 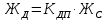(1.18)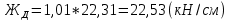 определяется интерполяцией по табл. 1 при μ = 0,2 и P_Т/P_a = f_c/y_a=4,88/3,4=1,43=1.Статическое напряжение, МПа: 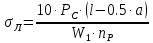(1.19) 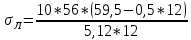= 487,63 (МПа)Расчетные статические напряжения в зоне края хомута, МПа: 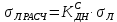(1.20) 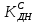принимается по табл. 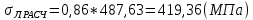1 при μ = 0,4 и P_c/P_a = 1.Амплитуда динамических напряжений, МПа: 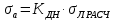(1.21) 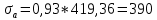(МПа) определяется интерполяцией по табл. 1 при μ = 0,2 и P_c/P_a = f_c/y_a.

2. 
   Расчет статических усилий, действующих на отдельные листы рессоры, и напряжений в них
   

Расчет прогибов для сечений, в которых оканчиваются листы коренной и ступенчатой части, см:

---

Смотрите также файлы

• Задание. Социальная ответственность профессиональной деятельности специалиста по рекламе и pr.docx

• Топологии сети.docx

• Изучение спроса и потребления лекарственных препаратов на примере аптечной организации.docx

• Основные способы продвижения турпродукта.doc

• Курсты Жмыс.docx