ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 109
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
айнымалы ток; 4)
Табыңыз: MN.
II. Геометриялық есепті шешудің мәні мен құрылымы
Мәселені шешу тек оның жауабын табу ғана емес. Егер сіз есептің шешімін талдасаңыз, оның жеке қадамдардан тұратынын көруге болады, ал шешудің әрбір қадамы математиканың кейбір жалпы позициясын (ережелер, заңдар, теоремалар, формулалар) есептің жеке шарттарына немесе осы шарттардан алынған салдарларға.
II. 1. Геометриялық есепті шығару нені білдіреді
Келесі мәселені шешуді қарастырыңыз:
Трапецияның табандарының ұзындығы 4см және 10см. Осы трапецияның орта сызығын диагональдарының бірі бөлетін кесінділердің ұзындықтарын табыңыз..
Алдымен осы есептің схемалық бейнесін құрастырайық (2-сурет):
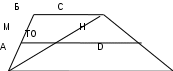
Күріш. 2
Берілген: AB||CD; AM=MD; BN=NC; AB=10см; CD = 4 см.
Табыңыз: MK және NK.
Шешуі: Трапецияның орта сызығы оның табандарына параллель. Демек, MN||AB және MN||CD. Диагональды айнымалы ток трапецияны екі үшбұрышқа бөледі. Олардың әрқайсысын қарастырайық. ABC үшбұрышында NK кесіндісі ортаңғы сызық болып табылады, өйткені MN кесіндісінің бөлігі ретінде NK AB-ге параллель, ал N нүктесі шарты бойынша ВС қабырғасының ортасы болады. Ал үшбұрыштың орта сызығы оның табанының жартысына тең. Бұл KN=0,5AB дегенді білдіреді, ал содан бері AB \u003d 10 см, содан кейін KN \u003d 5 см. Сол сияқты, ACD үшбұрышын ескере отырып, біз MK үшбұрыштың ортаңғы сызығы екенін анықтаймыз, сондықтан MK \u003d 0,5 CD, бірақ CD \u003d 4 см, сондықтан MK \u003d 2 см.
Жоғарыда келтірілген шешім келесі схема түрінде ұсынылуы мүмкін:
Жоғарыда келтірілген мысалдан келесі қорытынды жасауға болады:
Геометриялық есепті шешу дегеніміз математиканың жалпы ережелерінің (анықтамалар, аксиомалар, теоремалар, ережелер, заңдар, формулалар) тізбегін табу, оларды есеп шарттарына немесе олардың салдарына (шешудің аралық нәтижелері), Біз мәселеде не талап етілсе, соны аламыз, - деп жауап берді.
II. 2. Мәселені шешу процесінің құрылымы
Алдыңғы бөлімде біз есептердің шешімдерін жаздық, бірақ бұл шешімдер шешімнің өзін ғана көрсетті. Бірақ бұл шешімдер қалай табылды, олардың дұрыстығына қалай көз жеткіздіңіз? Егер мәселені шешу деп тапсырма алынған сәттен бастап оның шешімін толық аяқтағанға дейінгі процесті түсінетін болсақ, онда, анық, бұл процесс бұрыннан табылған шешімді ұсынудан ғана емес, сонымен қатар бірқатар шешімдерден тұрады. кезеңдері, олардың бірі шешімді ұсыну болып табылады.
Мәселені шешу процесінің қадамдары қандай?
Тапсырманы алғаннан кейін алдымен оның қандай тапсырма екенін, оның шарттары қандай екенін, оның талаптары қандай екенін анықтау керек, т.б. бірінші тарауда қарастырылғандай мәселені талдаңыз. Бұл талдау мәселені шешу процесінің бірінші кезеңін құрайды.
Ол талдау әйтеуір формалдануы, жазылуы керек. Ол үшін әр түрлі схемалық жазбалар қолданылады, олардың құрылысы мәселені шешу процесінің екінші кезеңін құрайды.
Мәселені талдау және оның схемалық бейнесін құру негізінен мәселені шешудің жолын табу үшін қажет. Бұл шешімді іздеу мәселені шешу процесінің үшінші кезеңі болып табылады.
Мәселені шешудің жолы, оны жүзеге асыру қажет болғанда – бұл мәселені шешу процесінің төртінші кезеңі – шешімді жүзеге асыру (сызбалау) кезеңі болады.
Шешім орындалып, айтылғаннан кейін (жазбаша немесе ауызша) бұл шешімнің дұрыстығына, мәселенің барлық талаптарын қанағаттандыратынына көз жеткізу керек. Ол үшін шешім тексеріледі, бұл мәселені шешу процесінің бесінші кезеңі.
Көптеген мәселелерді шешу кезінде тексеруден басқа, мәселені зерттеу қажет, атап айтқанда, қандай жағдайда мәселенің шешімі бар екенін және оның үстіне әрбір жеке жағдайда қанша әртүрлі шешімдер бар екенін анықтау; қандай жағдайда мәселенің шешімі мүлде жоқ және т.б. Мұның бәрі мәселені шешу процесінің алтыншы кезеңін құрайды.
Шешімнің дұрыстығына көз жеткізіп, қажет болған жағдайда мәселені зерттеуді жүзеге асырып, мәселенің жауабын нақты тұжырымдау қажет - бұл шешім процесінің жÐ
II. 3.1. Стандартты және стандартты емес тапсырмалар
Есептің тікелей шешімі кезекті қадамдардан (әрекеттерден) тұрады, олардың әрқайсысы математиканың қандай да бір жалпы позициясын есептің шарттарына немесе олардың салдарына қолдану болып табылады. Сондықтан осы қадамдарды табу мәселені шешу үшін ең маңызды нәрсе болып табылады. Математика сонымен қатар көптеген есептер үшін ережелерді белгілеумен айналысады, оның көмегімен берілген типтегі кез келген есепті шешу үшін қадамдар тізбегін орнатуға болады. Мұндай тапсырмалар стандартты деп аталады. Стандартты есептердің көптеген түрлері үшін мұндай ережелер бұрыннан табылған. Математикадағы бұл ережелер әртүрлі формада айтылады.
1.Ереже – анықтама: тікбұрышты үшбұрыштың сүйір бұрышының синусы – қарама-қарсы катеттің гипотенузаға қатынасы. Осы жерден синусты (демек, бұрышты) табу реті түсінікті: қарама-қарсы катетті табыңыз, гипотенузаны табыңыз, қатынасты табыңыз.
2. Ереже – теорема: трапецияның орта сызығы оның табандарына параллель және олардың жарты қосындысына тең. Шешу бағдарламасы қарапайым: негіздердің ұзындығын орнатыңыз, олардың жарты қосындысын табыңыз. Бұл трапецияның ортаңғы сызығының ұзындығы болады.
Стандартты есептерді шешу процесінің келесі ерекшеліктері бар:
1) Тапсырманы талдау берілген тапсырма жататын тапсырмалар түрін анықтауға (түрін тануға) дейін қысқарады.
2) Шешімді іздеу жалпы ереже немесе жалпы ереже негізінде бағдарлама – берілген типтегі есептерді шешуге арналған қадамдар тізбегін (егер мұндай бағдарлама математика курсында қарастырылмаса) құрастырудан тұрады. ). Әрине, бұл бағдарламаны жазбаша түрде тұжырымдаудың қажеті жоқ, оны өз санаңызда сипаттау жеткілікті.
3) Стандартты есепті шешудің өзі жалпы бағдарламаны берілген есептің шарттарына қолданудан тұрады. Егер шешу бағдарламасының кейбір қадамдары олардың орындалуы үшін кейбір бағдарламаларды да қажет етсе, онда оларға қатысты бірдей операциялар орындалады.
Бұдан шығатыны, стандартты есептерді оңай шешу үшін (және олар негізгі математикалық есептер болып табылады, ал қалғандарының барлығы оларға келтірілген):
- математика курсында оқытылатын барлық жалпы ережелерді (формулалар, сәйкестіктер) және жалпы ережелерді (анықтамалар мен теоремалар) есте сақтау (есте сақтау).
- сәйкес типтегі есептерді шешу қадамдарының реттілігін бағдарламаларға біріктірілген жалпы ережелерді, сәйкестіктерді, формулаларды, анықтамаларды және теоремаларды қолдана білу.
Стандартты емес есептер - бұл математика курсында оларды шешудің нақты бағдарламасын анықтайтын жалпы ережелер мен ережелер жоқ тапсырмалар. Оларды шешудің ерекшеліктерін білу үшін мысалды қарастырайық.
Табандары 12см және 20см, диагональдары өзара перпендикуляр болатын тең қабырғалы трапецияның ауданын табыңыз.
Шешуі: схемалық белгіні құрастыру.
Берілген: 1)AB||CD, 2)AD=BC, 3)AC ┴BD, 4)AB=20 см, 5)CD=12 см.
Табу:
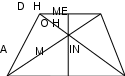
Күріш. 3
Трапецияның ауданын есептеу үшін Str формуласы бар. \u003d 0,5 (a + b) h, мұндағы a және b - трапеция табандарының ұзындығы, ал h - оның биіктігінің ұзындығы.
Трапецияның табандары берілген; сондықтан трапецияның биіктігін табу мәселесі қысқарады.
Трапецияның биіктігін салайық (3-сурет). Мұны келесідей орындау ыңғайлы: О нүктесі арқылы (диагональдардың қиылысуы) MN┴AB жүргіземіз. Сонда MN - қажетті биіктік h.
Өйткені трапеция тең қабырғалы, онда MN трапецияның симметрия осі, сондықтан М және N нүктелері сәйкес табандардың орта нүктелері болып табылады. Трапецияның табандарын біле отырып, AM=10 см, DN 6 см екенін табамыз. Сондай-ақ біз
AOM және DON үшбұрыштарын қарастырсақ, олардың тік бұрышты және тең қабырғалы екенін көреміз. Сонда ОМ = AM = 10см, ON = DN = 6см. Демек, h = MN = MO + ON = 10 + 6 = 16 см.
Енді көрсетілген формуланы қолдана отырып, біз трапецияның ауданын да есептей аламыз, біз Str. = 256 см2.
Бұл мәселені шешу процесі келесі қадамдардан тұрады:
6-мәселені шешіп, 2-есепке, содан кейін бастапқы есепке ораламыз.
Кез келген стандартты емес есепті шешу процесі екі негізгі операцияны дәйекті қолданудан тұрады:
1. Стандартты емес тапсырманы басқасына, оған баламалы, бірақ қазірдің өзінде стандартты тапсырмаға қысқарту (түрлендіру немесе қайта құру арқылы).
2. Стандартты емес тапсырманы бірнеше стандартты тапсырмаларға бөлу.
Стандартты емес тапсырманың сипатына қарай операциялардың біреуі немесе екеуі де қолданылады. Күрделі есептерді шешу кезінде бұл амалдар бірнеше рет қолданылады.
II. 3.2.Тапсырмалар түрін тану.
Мәселені шешуді бастағанда, ең алдымен мынаны анықтау керек: мәселе неде? Ол қандай тип? Басқаша айтқанда, сіз мәселенің түрін тануыңыз керек. Өйткені, мәселенің түрін біле отырып, көп жағдайда мәселені шешу әдісін бірден анықтауға болады, өйткені математика курсында есептердің көптеген түрлері үшін оларды шешудің жалпы ережелері бар. Барлық математикалық есептер, демек, геометриялық есептер жеке түрлерге немесе кластарға бөлінетін бірінші белгі есеп талаптарының сипаты болып табылады. Осы негізде тапсырмалар үш сыныпқа бөлінеді:
1. Іздегеніңді табуға арналған тапсырмалар. Бұл сыныптың есептерінде талап - қалағанды табу, тану. Сонымен бірге қажетті мән шама, қатынас, қандай да бір объект, объект, оның орны, пішіні және т.б. Геометриялық есептердің ішінен сегменттің ұзындығын, бұрыштың шамасын, фигураның ауданын, дененің көлемін және т.б. табу керек болатын есептеу есептері кіреді.
2. Дәлелдеуге немесе түсіндіруге арналған тапсырмалар.Бұл сыныптың тапсырмаларында қандай да бір тұжырымның дұрыстығын тексеру немесе бұл тұжырымның дұрыстығын немесе жалғандығын тексеру немесе ол немесе басқа құбылыстың, осы немесе басқа фактілердің неліктен орын алатынын түсіндіру талап етіледі. Талаптары «дәлелдеу», «тексеру» сөздерінен басталатын немесе «Неге?» деген сұрақты қамтитын барлық есептер әдетте осы есептер класына жатады.
3. Түрлендіру немесе салу тапсырмалары.Геометриялық есептердің бұл класына берілген шарттарды қанағаттандыратын қандай да бір фигураны түрлендіру немесе салу қажет болатын есептер жатады. Бұл кластың есептерінің сипатты ерекшелігі олардың әрқайсысында кейбір объектілер көрсетілген, олардан бұрын белгілі қасиеттері бар басқа объектіні құрастыру, тұрғызу қажет.
Есептің түрін белгілеу оны шешудің дайын жоспарын алуға мүмкіндік береді: ұқсас есептерді шешу үшін белгілі әдісті қолдану. Әрине, түрін анықтау мүмкін емес тапсырмалар бар, содан кейін басқа әдістерді қолдану керек (мысалы, белгілі типтегі қосалқы тапсырмаларға бөлу).
-
AM=MD; BN=NC.
Табыңыз: MN.
II. Геометриялық есепті шешудің мәні мен құрылымы
Мәселені шешу тек оның жауабын табу ғана емес. Егер сіз есептің шешімін талдасаңыз, оның жеке қадамдардан тұратынын көруге болады, ал шешудің әрбір қадамы математиканың кейбір жалпы позициясын (ережелер, заңдар, теоремалар, формулалар) есептің жеке шарттарына немесе осы шарттардан алынған салдарларға.
II. 1. Геометриялық есепті шығару нені білдіреді
Келесі мәселені шешуді қарастырыңыз:
Трапецияның табандарының ұзындығы 4см және 10см. Осы трапецияның орта сызығын диагональдарының бірі бөлетін кесінділердің ұзындықтарын табыңыз..
Алдымен осы есептің схемалық бейнесін құрастырайық (2-сурет):

Күріш. 2
Берілген: AB||CD; AM=MD; BN=NC; AB=10см; CD = 4 см.
Табыңыз: MK және NK.
Шешуі: Трапецияның орта сызығы оның табандарына параллель. Демек, MN||AB және MN||CD. Диагональды айнымалы ток трапецияны екі үшбұрышқа бөледі. Олардың әрқайсысын қарастырайық. ABC үшбұрышында NK кесіндісі ортаңғы сызық болып табылады, өйткені MN кесіндісінің бөлігі ретінде NK AB-ге параллель, ал N нүктесі шарты бойынша ВС қабырғасының ортасы болады. Ал үшбұрыштың орта сызығы оның табанының жартысына тең. Бұл KN=0,5AB дегенді білдіреді, ал содан бері AB \u003d 10 см, содан кейін KN \u003d 5 см. Сол сияқты, ACD үшбұрышын ескере отырып, біз MK үшбұрыштың ортаңғы сызығы екенін анықтаймыз, сондықтан MK \u003d 0,5 CD, бірақ CD \u003d 4 см, сондықтан MK \u003d 2 см.
Жоғарыда келтірілген шешім келесі схема түрінде ұсынылуы мүмкін:
| Жоқ. қадам | Математиканың жалпы ережелері | Мәселенің жағдайлары немесе олардың салдары | Нәтиже |
| 1 | Трапецияның орта сызығы оның табандарына параллель | ABCD трапециясының MN ортаңғы сызығы | MN||AB MN||CD |
| 2 | Диагональ трапецияны екі үшбұрышқа бөледі | ABCD – трапеция, АС – оның диагоналы | ABC және ACD үшбұрыштар |
| 3-4 | Үшбұрыштың екінші қабырғасына параллель қабырғасының ортасы арқылы өтетін кесінді үшбұрыштың орта сызығы болып табылады. | ABC үшбұрышында N нүктесі BC және MK||AB қабырғасының ортасы, үшбұрышта. ACD нүктесі M – AD және MK||CD ортасы | NK - үшбұрыштардың ортаңғы сызығы. ABC, MK – үшбұрыштардың ортаңғы сызығы. ACD |
| 5-6 | Үшбұрыштың орта сызығы табанының жартысы | NK – ABC үшбұрышының орта сызығы, АВ=10см; МК – ACD үшбұрышының орта сызығы, CD=4см | KN=0,5AB KN=5см MK=0,5CD, МК=2см. |
Жоғарыда келтірілген мысалдан келесі қорытынды жасауға болады:
Геометриялық есепті шешу дегеніміз математиканың жалпы ережелерінің (анықтамалар, аксиомалар, теоремалар, ережелер, заңдар, формулалар) тізбегін табу, оларды есеп шарттарына немесе олардың салдарына (шешудің аралық нәтижелері), Біз мәселеде не талап етілсе, соны аламыз, - деп жауап берді.
II. 2. Мәселені шешу процесінің құрылымы
Алдыңғы бөлімде біз есептердің шешімдерін жаздық, бірақ бұл шешімдер шешімнің өзін ғана көрсетті. Бірақ бұл шешімдер қалай табылды, олардың дұрыстығына қалай көз жеткіздіңіз? Егер мәселені шешу деп тапсырма алынған сәттен бастап оның шешімін толық аяқтағанға дейінгі процесті түсінетін болсақ, онда, анық, бұл процесс бұрыннан табылған шешімді ұсынудан ғана емес, сонымен қатар бірқатар шешімдерден тұрады. кезеңдері, олардың бірі шешімді ұсыну болып табылады.
Мәселені шешу процесінің қадамдары қандай?
Тапсырманы алғаннан кейін алдымен оның қандай тапсырма екенін, оның шарттары қандай екенін, оның талаптары қандай екенін анықтау керек, т.б. бірінші тарауда қарастырылғандай мәселені талдаңыз. Бұл талдау мәселені шешу процесінің бірінші кезеңін құрайды.
Ол талдау әйтеуір формалдануы, жазылуы керек. Ол үшін әр түрлі схемалық жазбалар қолданылады, олардың құрылысы мәселені шешу процесінің екінші кезеңін құрайды.
Мәселені талдау және оның схемалық бейнесін құру негізінен мәселені шешудің жолын табу үшін қажет. Бұл шешімді іздеу мәселені шешу процесінің үшінші кезеңі болып табылады.
Мәселені шешудің жолы, оны жүзеге асыру қажет болғанда – бұл мәселені шешу процесінің төртінші кезеңі – шешімді жүзеге асыру (сызбалау) кезеңі болады.
Шешім орындалып, айтылғаннан кейін (жазбаша немесе ауызша) бұл шешімнің дұрыстығына, мәселенің барлық талаптарын қанағаттандыратынына көз жеткізу керек. Ол үшін шешім тексеріледі, бұл мәселені шешу процесінің бесінші кезеңі.
Көптеген мәселелерді шешу кезінде тексеруден басқа, мәселені зерттеу қажет, атап айтқанда, қандай жағдайда мәселенің шешімі бар екенін және оның үстіне әрбір жеке жағдайда қанша әртүрлі шешімдер бар екенін анықтау; қандай жағдайда мәселенің шешімі мүлде жоқ және т.б. Мұның бәрі мәселені шешу процесінің алтыншы кезеңін құрайды.
Шешімнің дұрыстығына көз жеткізіп, қажет болған жағдайда мәселені зерттеуді жүзеге асырып, мәселенің жауабын нақты тұжырымдау қажет - бұл шешім процесінің жÐ
II. 3.1. Стандартты және стандартты емес тапсырмалар
Есептің тікелей шешімі кезекті қадамдардан (әрекеттерден) тұрады, олардың әрқайсысы математиканың қандай да бір жалпы позициясын есептің шарттарына немесе олардың салдарына қолдану болып табылады. Сондықтан осы қадамдарды табу мәселені шешу үшін ең маңызды нәрсе болып табылады. Математика сонымен қатар көптеген есептер үшін ережелерді белгілеумен айналысады, оның көмегімен берілген типтегі кез келген есепті шешу үшін қадамдар тізбегін орнатуға болады. Мұндай тапсырмалар стандартты деп аталады. Стандартты есептердің көптеген түрлері үшін мұндай ережелер бұрыннан табылған. Математикадағы бұл ережелер әртүрлі формада айтылады.
1.Ереже – анықтама: тікбұрышты үшбұрыштың сүйір бұрышының синусы – қарама-қарсы катеттің гипотенузаға қатынасы. Осы жерден синусты (демек, бұрышты) табу реті түсінікті: қарама-қарсы катетті табыңыз, гипотенузаны табыңыз, қатынасты табыңыз.
2. Ереже – теорема: трапецияның орта сызығы оның табандарына параллель және олардың жарты қосындысына тең. Шешу бағдарламасы қарапайым: негіздердің ұзындығын орнатыңыз, олардың жарты қосындысын табыңыз. Бұл трапецияның ортаңғы сызығының ұзындығы болады.
Стандартты есептерді шешу процесінің келесі ерекшеліктері бар:
1) Тапсырманы талдау берілген тапсырма жататын тапсырмалар түрін анықтауға (түрін тануға) дейін қысқарады.
2) Шешімді іздеу жалпы ереже немесе жалпы ереже негізінде бағдарлама – берілген типтегі есептерді шешуге арналған қадамдар тізбегін (егер мұндай бағдарлама математика курсында қарастырылмаса) құрастырудан тұрады. ). Әрине, бұл бағдарламаны жазбаша түрде тұжырымдаудың қажеті жоқ, оны өз санаңызда сипаттау жеткілікті.
3) Стандартты есепті шешудің өзі жалпы бағдарламаны берілген есептің шарттарына қолданудан тұрады. Егер шешу бағдарламасының кейбір қадамдары олардың орындалуы үшін кейбір бағдарламаларды да қажет етсе, онда оларға қатысты бірдей операциялар орындалады.
Бұдан шығатыны, стандартты есептерді оңай шешу үшін (және олар негізгі математикалық есептер болып табылады, ал қалғандарының барлығы оларға келтірілген):
- математика курсында оқытылатын барлық жалпы ережелерді (формулалар, сәйкестіктер) және жалпы ережелерді (анықтамалар мен теоремалар) есте сақтау (есте сақтау).
- сәйкес типтегі есептерді шешу қадамдарының реттілігін бағдарламаларға біріктірілген жалпы ережелерді, сәйкестіктерді, формулаларды, анықтамаларды және теоремаларды қолдана білу.
Стандартты емес есептер - бұл математика курсында оларды шешудің нақты бағдарламасын анықтайтын жалпы ережелер мен ережелер жоқ тапсырмалар. Оларды шешудің ерекшеліктерін білу үшін мысалды қарастырайық.
Табандары 12см және 20см, диагональдары өзара перпендикуляр болатын тең қабырғалы трапецияның ауданын табыңыз.
Шешуі: схемалық белгіні құрастыру.
Берілген: 1)AB||CD, 2)AD=BC, 3)AC ┴BD, 4)AB=20 см, 5)CD=12 см.
Табу:
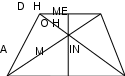
Күріш. 3
Трапецияның ауданын есептеу үшін Str формуласы бар. \u003d 0,5 (a + b) h, мұндағы a және b - трапеция табандарының ұзындығы, ал h - оның биіктігінің ұзындығы.
Трапецияның табандары берілген; сондықтан трапецияның биіктігін табу мәселесі қысқарады.
Трапецияның биіктігін салайық (3-сурет). Мұны келесідей орындау ыңғайлы: О нүктесі арқылы (диагональдардың қиылысуы) MN┴AB жүргіземіз. Сонда MN - қажетті биіктік h.
Өйткені трапеция тең қабырғалы, онда MN трапецияның симметрия осі, сондықтан М және N нүктелері сәйкес табандардың орта нүктелері болып табылады. Трапецияның табандарын біле отырып, AM=10 см, DN 6 см екенін табамыз. Сондай-ақ біз
AOM және DON үшбұрыштарын қарастырсақ, олардың тік бұрышты және тең қабырғалы екенін көреміз. Сонда ОМ = AM = 10см, ON = DN = 6см. Демек, h = MN = MO + ON = 10 + 6 = 16 см.
Енді көрсетілген формуланы қолдана отырып, біз трапецияның ауданын да есептей аламыз, біз Str. = 256 см2.
Бұл мәселені шешу процесі келесі қадамдардан тұрады:
-
трапецияның ауданын есептеу мәселесі трапеция биіктігін табу мәселесіне дейін қысқарды; -
трапеция биіктігін табу тапсырмасы екі қосалқы тапсырмаға бөлінді: а) MN биіктігінің ОМ кесіндісін табу; б) бірдей биіктіктегі ON кесіндісінің ұзындығын табу; -
2 (а, б) тапсырмалары екі тапсырмаға қысқартылды: а) берілген трапецияға қатысты MN түзуінің формасын тану; б) AOM және DON үшбұрыштарының ОМ және ON қабырғаларын анықтау; -
3(а) есебін шешу нәтижесінде MN трапецияның симметрия осі екенін анықтадық. Бұл AM және DN, сондай-ақ AOM және DON бұрыштарын табуға мүмкіндік береді; -
4 есепті шешу нәтижелері және трапеция диагональдарының перпендикулярлық шарты AOM және DON үшбұрыштарының тік бұрышты және тең қабырғалы екенін анықтауға мүмкіндік береді; -
Демек, 3 (б) есеп келесіге дейін қысқарады: егер екінші катет белгілі болса, тік бұрышты тең қабырғалы үшбұрыштың катетін табыңыз.
6-мәселені шешіп, 2-есепке, содан кейін бастапқы есепке ораламыз.
Кез келген стандартты емес есепті шешу процесі екі негізгі операцияны дәйекті қолданудан тұрады:
1. Стандартты емес тапсырманы басқасына, оған баламалы, бірақ қазірдің өзінде стандартты тапсырмаға қысқарту (түрлендіру немесе қайта құру арқылы).
2. Стандартты емес тапсырманы бірнеше стандартты тапсырмаларға бөлу.
Стандартты емес тапсырманың сипатына қарай операциялардың біреуі немесе екеуі де қолданылады. Күрделі есептерді шешу кезінде бұл амалдар бірнеше рет қолданылады.
II. 3.2.Тапсырмалар түрін тану.
Мәселені шешуді бастағанда, ең алдымен мынаны анықтау керек: мәселе неде? Ол қандай тип? Басқаша айтқанда, сіз мәселенің түрін тануыңыз керек. Өйткені, мәселенің түрін біле отырып, көп жағдайда мәселені шешу әдісін бірден анықтауға болады, өйткені математика курсында есептердің көптеген түрлері үшін оларды шешудің жалпы ережелері бар. Барлық математикалық есептер, демек, геометриялық есептер жеке түрлерге немесе кластарға бөлінетін бірінші белгі есеп талаптарының сипаты болып табылады. Осы негізде тапсырмалар үш сыныпқа бөлінеді:
1. Іздегеніңді табуға арналған тапсырмалар. Бұл сыныптың есептерінде талап - қалағанды табу, тану. Сонымен бірге қажетті мән шама, қатынас, қандай да бір объект, объект, оның орны, пішіні және т.б. Геометриялық есептердің ішінен сегменттің ұзындығын, бұрыштың шамасын, фигураның ауданын, дененің көлемін және т.б. табу керек болатын есептеу есептері кіреді.
2. Дәлелдеуге немесе түсіндіруге арналған тапсырмалар.Бұл сыныптың тапсырмаларында қандай да бір тұжырымның дұрыстығын тексеру немесе бұл тұжырымның дұрыстығын немесе жалғандығын тексеру немесе ол немесе басқа құбылыстың, осы немесе басқа фактілердің неліктен орын алатынын түсіндіру талап етіледі. Талаптары «дәлелдеу», «тексеру» сөздерінен басталатын немесе «Неге?» деген сұрақты қамтитын барлық есептер әдетте осы есептер класына жатады.
3. Түрлендіру немесе салу тапсырмалары.Геометриялық есептердің бұл класына берілген шарттарды қанағаттандыратын қандай да бір фигураны түрлендіру немесе салу қажет болатын есептер жатады. Бұл кластың есептерінің сипатты ерекшелігі олардың әрқайсысында кейбір объектілер көрсетілген, олардан бұрын белгілі қасиеттері бар басқа объектіні құрастыру, тұрғызу қажет.
Есептің түрін белгілеу оны шешудің дайын жоспарын алуға мүмкіндік береді: ұқсас есептерді шешу үшін белгілі әдісті қолдану. Әрине, түрін анықтау мүмкін емес тапсырмалар бар, содан кейін басқа әдістерді қолдану керек (мысалы, белгілі типтегі қосалқы тапсырмаларға бөлу).