ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 288
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Мұғалімнің аты-жөні: | Ұ.Қайназар | |||||
| Пән/ геометрия | 9 сынып | |||||
| Күні:28.03.2023 ж | | |||||
| Тарау немесе бөлім атауы: | 9.4АШеңбер. Көпбұрыштар. | |||||
| Сабақтың тақырыбы: | Шеңбер және дөңгелек. Доғаның ұзындығы. Дөңгелек, сектор және сегменттің аудандары | |||||
| Оқу мақсаты: | 9.1.1.1 доға ұзындығының формуласын қорытып шығару және қолдану; | |||||
| Бағалау критериі: |
| |||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |
| 3 минут | Ұйым дастыру | Сәлеметсіздерме! Бүгін, Шеңбер және дөңгелек. Доғаның ұзындығы. Дөңгелек, сектор және сегменттің аудандары тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз:
«Допты лақтыру» әдісі арқылы өткен сабақты 3 топ бір-біріне алдыңғы тақырыптар бойынша сұрақтар қояды 1. Косинустар теоремасын тұжырымдаңдар. 2. Үшбұрыштың тамаша нүктесі? 3. Үшбұрыштарды шешу деп нені түсінесіңдер? 4. Пифагор теоремасы? 5. Синустар теоремасын дәлеледеп беріңдер. 6.Үшбұрыш ауданы неге тең? Бағалау: Ауызша бағалау. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді Тест тапсырмаларын орындайды |  | | |
| 5 мин | Жаңа сабақ | Анықтама. Шеңберден және жазықтықтың осы шеңбермен шектелген бөлігінен тұратын фигураны дөңгелек дейміз. S = ПR2 Анықтама. Центрлік бұрышпен және ол тірелетін доғамен шектелген дөңгелектің бөлігі дөңгелек сектор деп аталады. ОА және ОВ радиустары дөңгелекті 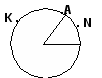 III топ. Анықтама. Шеңбердің доғасымен және осы доғаның ұштарын қосатын хордамен шектелген дөңгелектің бөлігін сегмент деп аталады. АВ хордасы дөңгелекті екі сегментке – АКВ және АNB сегменттеріне бөледі. Егер хорда диаметр болса, онда ол дөңгелекті екі жарты дөңгелекке бөледі. АNB сегменттің ауданы О АNB сектордың ауданынан АОВ үшбұрышының ауданын шегеріп тастағанға тең екенін көреміз. Сектордың ауданын табу формуласын (3) ескеріп және (4), (5) формулаларды біріктіріп, сегменттің ауданын табу формуласын жалпы түрде жазамыз: 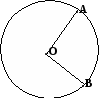 .N Мұндағы R – дөңгелектің радиусы, | Тақырып бойынша ресурстарды қарап, танысады 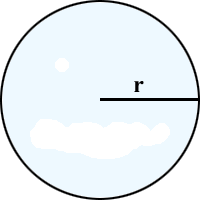 Қажетті анықтамаларды жазып, сызбаны сызады. | | Интернет ресурстары | |
| 20 минут | Бекіту тапсырмасы | А деңгейі. №1 1)Берілгені: Табу керек: S - ? Шешуі: №2. 1) Берілгені: Табу керек: Шешуі: В деңгейі. №3. Радиусы 4 см, ал доғасының радиандық өлшемі: а) ; ә) 1,2 рад болатын сектордың ауданын табыңдар. Шешуі: А)Берілгені: R = 4см α = Табу керек: Sсектр. - ? Жауабы: S = см2 Ә) Берілгені: R = 4см α = 1.2 Табу керек: Sсектр. - ? S = Оқулықпен жұмыс. № 1-5 есептер | Оқушылар есептің сызбасын сызады. Берілген тапсырма бойынша есепті орындайды Оқулықтан есеп шығарады. | Дескриптор -Дөңгелек ауданының формуласын біледі; -Есептеу жүргізеді. ҚБ.«Смайлик әдісі». -Барлығы түсінікті -Жартылай түсінікті -Түсінген жоқпын Дескриптор. -Берілгені бойынша шартты дұрыс жазады. -Сектордың ауданының формуласын дұрыс қолданады. -Есептейді, жауабын есептейді. -Жауабын табады. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |
| 10мин | Жеке жұмыс | Есептер жинағынан тапсырмалар орындайды | Қосымша дәптерде тапсырманы орындайды. | | Есептер жинағы | |
| 2 минут | |
Кері байланыс: Ауызша кері байланыс жүргіземін. Үйге тапсырма. № 6 есеп | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Презен тация | |
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||||||||||
| Пән/Сынып: | 9 сынып | |||||||||||||||
| Күні: | | |||||||||||||||
| Тарау немесе бөлім атауы: | 9.4АШеңбер. Көпбұрыштар. | |||||||||||||||
| Сабақтың тақырыбы: | Шеңбер және дөңгелек. Доғаның ұзындығы. Дөңгелек, сектор және сегменттің аудандары | |||||||||||||||
| Оқу мақсаты: | 9.1.1.1 доға ұзындығының формуласын қорытып шығару және қолдану; | |||||||||||||||
| Бағалау критериі: |
| |||||||||||||||
| Саралап оқыту тапсырмалары | ||||||||||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||||||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||||||||||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Шеңбер және дөңгелек. Доғаның ұзындығы. Дөңгелек, сектор және сегменттің аудандары тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз:
Үй тапсырмасын тексеру.«Сәйкестендіру кестесі» арқылы орындалады «Досыңды тексер» әдісімен оқушылар бір-бірін тексереді.дұрыс сәйкестендіру кестесі тақтада жазылады.
|
||||||||||||||
| Амандасады, тақырыпты жазады. Сұрақтарға жауап береді Тест тапсырмаларын орындайды |  | Whatsapp месенжерін қолдану. | ||||||||||||
| 5 мин | Жаңа сабақ | Доға ұзындығы Ш Центрлік бұрыш шамасы радиан арқылы берілген жағдайда қарастырамын.Шамасы 1 радианға тең центрлік бұрышқа тірелген доғаның ұзындығы шеңбер ұзындығының бөлігіне тең, яғни болады.Онда шамасы радианға тең центрлік бұрышқа сәйкес шеңбер доғасының ұзындығы формуласымен есептейді. | Тақырып бойынша ресурстарды қарап, танысады  Қажетті анықтамаларды жазып, сызбаны сызады. | | Интернет ресурстары | |||||||||
| 20 минут | Бекіту тапсырмасы | №1. Шеңбердің R=2см.
№2. Сектор ауданын формуласын қорытып шығарыңыз. Есеп : Дөңгелектің радуисы 1-ге тең. 900, 1200 центрлік бұрышқа сәйкес сектордың ауданын табыңыз? №3. 1. Диаметрі 10 см дөңгелек болатын және 1800 доғаға сәйкес сегменттің ауданын табыңдар. 2. Сектордың ауданы 16см2 және 900 доғаға сәйкес дөңгелектің радуисын табыңдар. Оқулықпен жұмыс. № Сергіту сәті. Көк құтанша ақ айдында, Бір аяқпен тұрады. Тұмсығымен ол мұнда , Шыр айналып шығады. (циркуль) | Оқушылар есептің сызбасын сызады. Берілген тапсырма бойынша есепті орындайды Оқулықтан есеп шығарады. | Дескриптор: Білім алушы. - 1.Доғаның ұзындығының формуласын тұжырымдайды 2.Есептеулерді орындайды 3.Жауабын табады Дескриптор. Білім алушы. -Берілгені бойынша шартты дұрыс жазады. -Сектордың, сегменттің ауданының формуласын дұрыс қолданады. -Есептейді, жауабын есептейді. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||||||||
| 10мин | Жеке жұмыс | Тапсырма 1. Шеңбердің радиусы 8см. 1. Шеңбердің ұзындығын табыңыз. 2. Жарты доғаның ұзындығын табыңыз. 3. 900 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 4. 600 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 5. 420 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 6.Кез келген центрлік бұрышқа сәйкес доғаның ұзындығын қалай табуға болады? Есептер жинағынан тапсырмалар орындайды | Тапсырманы орындайды. | | Есептер жинағы | |||||||||
| 2 минут | |
Кері байланыс:
Үйге тапсырма. № | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||||||||
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||||||||
| Пән/Сынып: | 9 сынып | |||||||||||||
| Күні: | | |||||||||||||
| Тарау немесе бөлім атауы: | 9.4АШеңбер. Көпбұрыштар. | |||||||||||||
| Сабақтың тақырыбы: | Іштей сызылған бұрыш анықтамасы және оның қасиеттері | |||||||||||||
| Оқу мақсаты: | 9.1.1.3 іштей сызылған бұрыш анықтамасын және оның қасиеттерін білу; | |||||||||||||
| Бағалау критериі: | -Іштей сызылған бұрыш анықтамасы біледі; -Іштей сызылған бұрыштың қасиеттерін түсінеді; | |||||||||||||
| Саралап оқыту тапсырмалары | ||||||||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||||||||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Шеңбер және дөңгелек. Доғаның ұзындығы. Дөңгелек, сектор және сегменттің аудандары тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Іштей сызылған бұрыш анықтамасы біледі; -Іштей сызылған бұрыштың қасиеттерін түсінеді; Үй тапсырмасын тексеру. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді |  | Whatsapp месенжерін қолдану. | |||||||||
| 5 мин | Жаңа сабақ | Жаңа тақырыпты түсіндіру. Б 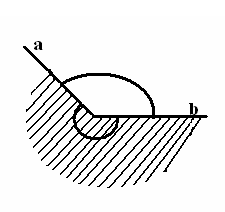 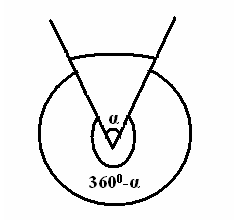 ұрыш жазықтықты екі бөлікке бөледі. Бұл бөліктердің әр қайсысы бұрыш деп аталады. Қабырғалары а және b сәулелері болатын АОВ және ВОА бұрыштары кескінделген. Қабырғалары ортақ бұрыштар бір-біріне толықтауыш бұрыштар деп аталады. ВОА бұрышы АОВ бұрышына немесе АОВ бұрышы ВОА бұрышына толықтауыш бұрыштар. ұрыш жазықтықты екі бөлікке бөледі. Бұл бөліктердің әр қайсысы бұрыш деп аталады. Қабырғалары а және b сәулелері болатын АОВ және ВОА бұрыштары кескінделген. Қабырғалары ортақ бұрыштар бір-біріне толықтауыш бұрыштар деп аталады. ВОА бұрышы АОВ бұрышына немесе АОВ бұрышы ВОА бұрышына толықтауыш бұрыштар. Егер бұрыштардың біреуінің градустық өлшемі α – ға тең болса, онда толықтауыш бұрыштың градустық өлшемі 3600- α болады. Төбесі шеңбердің центрінде жататын бұрыш центрлік бұрыш деп аталады. Бұрыштың ішінде орналасқан шеңбер бөлігі осы центрлік бұрышқа сәйкес шеңбер доғасы деп аталады. 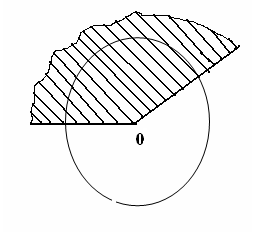 АКВ доғасы АОВ центрлік бұрышына сәкес. Шеңбер доғасының градустық өлшемі деп оған сәйкес центрлік бұрыштың градустық өлшемін атайды. АКВ доғасы АОВ центрлік бұрышына сәкес. Шеңбер доғасының градустық өлшемі деп оған сәйкес центрлік бұрыштың градустық өлшемін атайды. 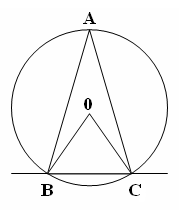 Төбесі шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін бұрыш шеңберге іштей сызылған бұрыш деп аталады. Төбесі шеңберде жататын, ал қабырғалары сол шеңберді қиып өтетін бұрыш шеңберге іштей сызылған бұрыш деп аталады. АВС бұрышы шеңберге іштей сызылған . Оның В төбесі шеңбер бойында жатыр, ал бұрыштың қабырғалары шеңберді А және С нүктелерінде қиып өтеді. А және С нүктелері шеңберді екі доғаға бөледі. В нүктесі жатпайтын доғаға сәйкес центрлік бұрыш іштей сызылған В бұрышына сәйкес центрлік бұрыш деп аталады. Сонымен шеңберге іштей сызылған АВС бұрышына сәйкес центрлік бұрыш АОС бұрышы болады. Теорема: Шеңберге іштей сызылған бұрыш өзіне сәйкес центрлік бұрыштың жартысына тең болады. Теореманы дәлелдеу үшін 3 жағдайды қарастырамыз: 1. Бұрыштың бір қабырғасы шеңбердің центрінен өтеді. АО радиусын жүргізсек, теңбүйірлі АВО үшбұрышы шығады, мұнда АО=ОВ, сондықтан 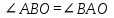 . 2∙∟АВО=∟AOD AOD бұрышы АВО бұрышына қатысты сыртқы бұрыш, сондықтан ол АВО және ВАО бұрыштарының қосындысына тең, яғни екі еселенген АВО бұрышына тең: . 2∙∟АВО=∟AOD AOD бұрышы АВО бұрышына қатысты сыртқы бұрыш, сондықтан ол АВО және ВАО бұрыштарының қосындысына тең, яғни екі еселенген АВО бұрышына тең: 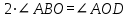 . Осы себепті АВО бұрышы AOD центрлік бұрышының жартысына тең: . Осы себепті АВО бұрышы AOD центрлік бұрышының жартысына тең: 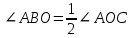 . . 2. Шеңбердің О центрі шеңберге іштей сызылған бұрыш қабырғаларының арасында жатады. ВD диаметрін жүргіземіз, сонда  . .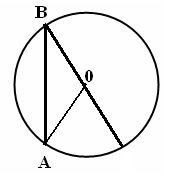 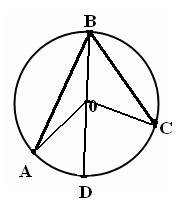 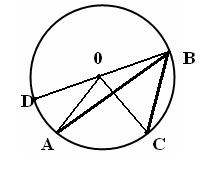 3. Шеңбердің О центрі шеңберге іштей сызылған АВС бұрышынан тысқары жатсын. ВD диаметрін жүргіземіз, сонда 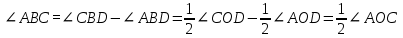 . .Теорема дәлелденді. | Тақырып бойынша ресурстарды қарап, танысады  Қажетті анықтамаларды жазып, сызбаны сызады. | | Интернет ресурстары | |||||||||
| 20 минут | Бекіту тапсырмасы | Оқулықпен жұмыс. №1, №3, №5, №6. Тест тапсырмалары 1).10 бұрыштың неше диагоналі бар? А) 7; В)30; С) 54 Д) 35 2) Көпбұрыштың бір төбесінен 16 диагональ жүргізуге болады. Бұл қандай көпбұрыш? А) 21; В) 20; С) 104 Д) 13 3) Сегізбұрыштың ішкі бұрыштарының қосындысы неге тең? А) 360; В) 1080; С) 1440; Д) 135 4) Он екі бұрыштың әр төбесінен неше диагональ жүргізуге болады? А)10 В)8 С) 7 Д) 9 Е)5 5)Дұрыс бесбұрыштың әр бұрышы? А) 3600 В) 900 С) 5400 Д) 1080 Е) 1200 6)Бір бұрышы 1440-қа тең көбұрыштың қабырғалар саны неге тең? А) 10 В) 12 С) 8 Д) 9 7)Бір доғаға тірелетін, АОВ центрлік бұрышы үшін іштей сызылған АОВ бұрышының градустық өлшемін табыңыз. АСВ бұрышы 800-қа тең. 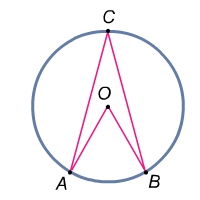 А) 600 В) 400 С) 1600 Д) 1800 Е) 1200 | Оқулықтан есеп шығарады. Оқушылар есептің сызбасын сызады. Берілген тапсырма бойынша есепті орындайды | Дескриптор: Білім алушы. - 1.Доғаның ұзындығының формуласын тұжырымдайды 2.Есептеулерді орындайды 3.Жауабын табады Дескриптор. Білім алушы. -Берілгені бойынша шартты дұрыс жазады. -Сектордың, сегменттің ауданының формуласын дұрыс қолданады. -Есептейді, жауабын есептейді. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||||||||
| 10мин | Жеке жұмыс | Тапсырма 1. Шеңбердің радиусы 8см. 1. Шеңбердің ұзындығын табыңыз. 2. Жарты доғаның ұзындығын табыңыз. 3. 900 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 4. 600 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 5. 420 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 6.Кез келген центрлік бұрышқа сәйкес доғаның ұзындығын қалай табуға болады? Есептер жинағынан тапсырмалар орындайды | Тапсырманы орындайды. | | Есептер жинағы | |||||||||
| 2 минут | |
1. Центірлік бұрыш дегеніміз не? 2. Центрлік бұрышқа сәйкес шеңбер доғасы деп қандай доғаны айтады? 3. Шеңбер доғасының градустық өлшемі қалай анықталады? 4. Шеңберге іштей сызылған бұрыш деп қандай бұрышты атайды? Кері байланыс:
Үйге тапсырма. №7. | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||||||||
Сабақ жоспары
Бекітемін:
| Мұғалімнің аты-жөні: | | |||||||||||||
| Пән/Сынып: | 9 сынып | |||||||||||||
| Күні: | | |||||||||||||
| Тарау немесе бөлім атауы: | 9.4АШеңбер. Көпбұрыштар. | |||||||||||||
| Сабақтың тақырыбы: | Іштей сызылған бұрыш анықтамасы және оның қасиеттері | |||||||||||||
| Оқу мақсаты: | 9.1.1.3 іштей сызылған бұрыш анықтамасын және оның қасиеттерін білу; | |||||||||||||
| Бағалау критериі: | -Іштей сызылған бұрыш анықтамасы біледі; -Іштей сызылған бұрыштың қасиеттерін түсінеді; | |||||||||||||
| Саралап оқыту тапсырмалары | ||||||||||||||
| Ұжымдық жұмыс Жаңа тақырыптың түсіндірілуі Сабақ мақсаты мен бағалау критерийлерін таныстыру; Бейнероликті қолдана отырып, бекіту тапсырмаларын орындату | Бірлескен жұмыс (1,2,3 тапсырма) Тапсырманы ұсыну және дұрыс жауапты ұсыну арқылы үйрету Бекітуге арналғантапсырмаларды орындату; Тапсырмалардың жауаптарын жазу. | Жеке жұмыс Тапсырманы ұсыну, оқушылар өз бетімен орындауы | ||||||||||||
| Уақыты | Кезең дері | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | |||||||||
| 3 минут | Ұйымдастыру | Сәлеметсіздерме! Бүгін, Шеңбер және дөңгелек. Доғаның ұзындығы. Дөңгелек, сектор және сегменттің аудандары тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: -Іштей сызылған бұрыш анықтамасы біледі; -Іштей сызылған бұрыштың қасиеттерін түсінеді; Үй тапсырмасын тексеру. | Амандасады, тақырыпты жазады. Сұрақтарға жауап береді |  | Whatsapp месенжерін қолдану. | |||||||||
| 5 мин | Жаңа сабақ | 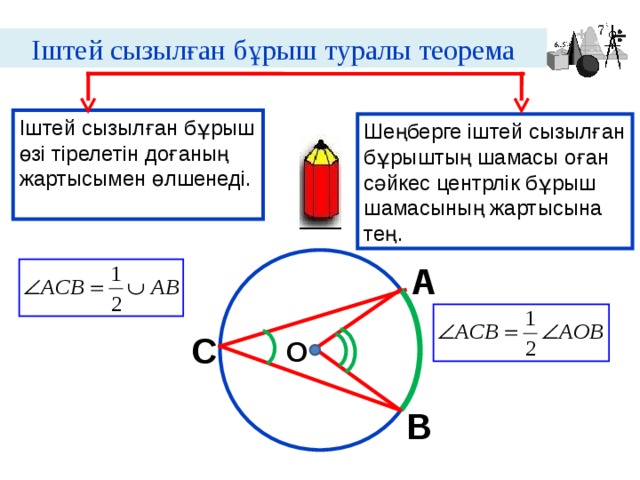 | Тақырып бойынша ресурстарды қарап, танысады  Қажетті анықтамаларды жазып, сызбаны сызады. | | Интернет ресурстары | |||||||||
| 20 минут | Бекіту тапсырмасы | Оқулықпен жұмыс. №1, №3, №5, №6. №1. АВС бұрышы шеңберге іштей сызылған. Оған сәйкес центрлік бұрыш 88°-қа тең. АВС бұрышын тап. Шешуі: шеңберге іштей сызылған бұрыш өзіне сәйкес центлік бұрыштың жартысына тең демек 88/2=44 №2. Шеңберге іштей сызылған бұрыш 22030/ - қа тең. Осы бұрыш тірелетін доғаның градустық шамасын есептеңдер. №3 Шеңбер хордаларымен 1:2:3 қатынасында бөлінген. Пайда болған үшбұрыштың бұрыштарын есептеңдер. №4. Іштей сызылған АВС бұрышы АС доғасына тіреледі. АС доғасы 570- қа тең. АВС бұрышы неге тең? В-тобы:Тест тапсырмалары 1) Сегізбұрыштың ішкі бұрыштарының қосындысы неге тең? А) 360; В) 1080; С) 1440; Д) 135 2) Он екі бұрыштың әр төбесінен неше диагональ жүргізуге болады? А)10 В)8 С) 7 Д) 9 Е)5 3)Дұрыс бесбұрыштың әр бұрышы? А) 3600 В) 900 С) 5400 Д) 1080 Е) 1200 4)Бір бұрышы 1440-қа тең көбұрыштың қабырғалар саны неге тең? А) 10 В) 12 С) 8 Д) 9 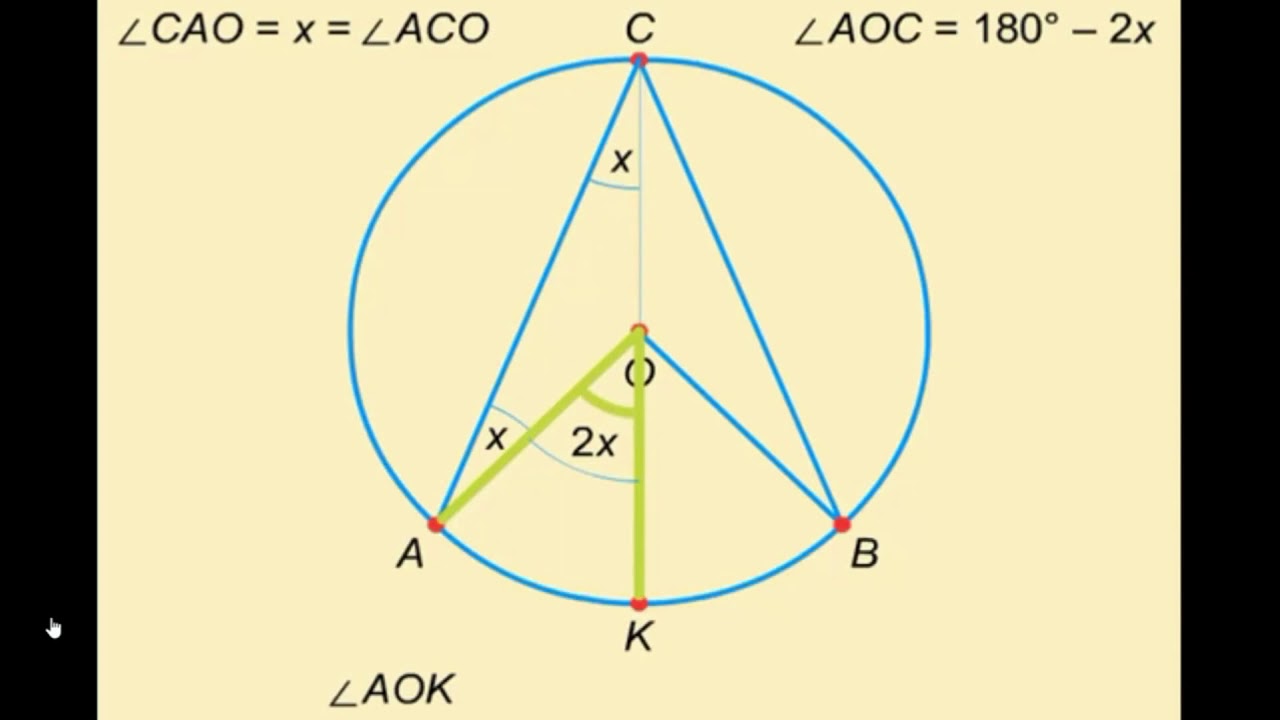 | Оқулықтан есеп шығарады. Оқушылар есептің сызбасын сызады. Берілген тапсырма бойынша есепті орындайды | Дескриптор: Білім алушы. - 1.Доғаның ұзындығының формуласын тұжырымдайды 2.Есептеулерді орындайды 3.Жауабын табады Дескриптор. Білім алушы. -Берілгені бойынша шартты дұрыс жазады. -Сектордың, сегменттің ауданының формуласын дұрыс қолданады. -Есептейді, жауабын есептейді. | Слайд Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: В.А.Смирнов, Е.А.Тұяқов Алматы «Мектеп» баспасы 2019 жыл Интернет ресурстары | |||||||||
| 10мин | Жеке жұмыс | Тапсырма 1. Шеңбердің радиусы 3,5 см. 1. Шеңбердің ұзындығын табыңыз. 2. Жарты доғаның ұзындығын табыңыз. 3. 1500 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 4. 1350 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 5. 800 –тық центрлік бұрышқа сәйкес доғаның ұзындығын табыңыз. 6.Кез келген центрлік бұрышқа сәйкес доғаның ұзындығын қалай табуға болады? Есептер жинағынан тапсырмалар орындайды | Тапсырманы орындайды. | | Есептер жинағы | |||||||||
| 2 минут | |
1. Центірлік бұрыш дегеніміз не? 2. Центрлік бұрышқа сәйкес шеңбер доғасы деп қандай доғаны айтады? 3. Шеңбер доғасының градустық өлшемі қалай анықталады? 4. Шеңберге іштей сызылған бұрыш деп қандай бұрышты атайды? Кері байланыс:
Үйге тапсырма. №15. | Тақырыпты меңгергенін анықтау Кері байланыс жасайды. |  | Whatsapp месенжерін қолдану Презентация | |||||||||