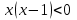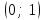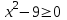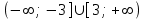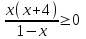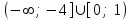Қысқа мерзімді жоспар Тексерілді:

Сабақтың тақырыбы: Рационал теңсіздік

Бөлімі:	Квадрат теңсіздік
Педагогтің аты-жөні:	Cуттибаева М
Күні:	10.04.2023
Сыныбы: 8	Қатысушылар саны: Қатыспағандар саны:
Сабақтың тақырыбы:	Рационал теңсіздік
Оқу бағдарламасына сәйкес оқу мақсаты:	8.2.2.9рационал теңсіздіктерді шешу
Сабақтың мақсаты:	рационал теңсіздіктерді шешу үйрену

Сабақтың барысы:

Сабақ кезеңі/ Уақыты	Педагогтің іс-әрекеті	Оқушының іс-әрекеті	Бағалау	Ресурстар
Сабақтың басы Өткен сабақты тексеру 5 мин.	Ұйымдаcтырy кезеңi:  Жалпы  cыныппен жұмыc. (оқyшылармен амандаcy, оларды түгендеy, cабаққа cәттiлiк тiлеy ) Үй тапсырмасын тексеру .Сызықтық теңсіздіктерді қасиеттері қандай? 2. Cызықтық теңсіздіктерді қалай шешеміз? 3.Квадрат теңдеуді шешу әдістері қандай	«Жақсы тілек- жан жылуы» оқушылар бір-бірлеріне тілектер айтып, жақсы көңіл күймен сабақты бастайды. Оқушылар сұрақтарға жауап береді. Мысалдар келтіреді. Оқушылар сұрақтарға жауап береді	Дескриптор: -Өткен сабақтағы ережелерді қайталайды.
Сабақтың ортасы 35 мин. ЕББҚ	. 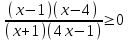түрінде жазамыз. Осы теңсіздікке аралықтар тәсілін қолдану үшін бөлшектің алымы мен бөліміндегі жай көбейткішті нөлге айналдыратын -2; 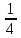; 1; 4 нүктелерімен сан өсін 5 бөлікке бөлеміз. Жауабы: х 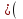- 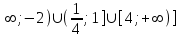1 тапсырма: «Ойлан-жұптас-бөліс» белсенді әдісі арқылы білімді жинақтау , ынтымақтаса отырып өз ойларын еркін жеткізе алады. а) х2-4х+3>0 ә) (х-4)(х+3)≤0 б) 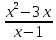≥0 Дескриптор: функцияның нөлдерін табады; ММЖ анықтайды; координаталық осьте белгілейді; функцияның таңбасын анықтайды; шешімін жазады. ҚБ: «Бас бармақ» әдісі Сұрақтар: 1)Тапсырмаларды орындау барысында қиындық туғызған қандай сұрақтар? 2)Шешімін жазған кезде қандай қателіктер кетті? (Т) 2 тапсырма: «Ойынды жалғастыр» белсенді әдісін қолданамын,себебі алдыңғы білімді бекіте отырып,тереңдеу, талдау мақсатын негізге алдым. 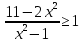теңсіздігін шешіп, бүтін шешімдерін тап. Дескриптор: P(х)≥ 0 түріне келтіреді; ММЖ анықтайды; интервалдар әдісін қолданады; шешімін жазады; бүтін шешімін табады «Сәйкестігін тап» Теңсіздіктерге бірнеше артық жауаптар беріледі. Оқушы есепті шығарып, ішінен дұрыс жауапты сол тұсқа жапсырады. 1 А 2 В 3 С 4 Д 5 Е	Түсінбеген тапсырмаларды бір- біріне түсіндіреді. Топтар келесі топтың тапсырмасын алмасып тексереді. Ерте аяқтаған топ тақтада қорғайды Берілген тапсырма бойынша есепті орындайды Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, топтық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп кестені толтырады. Оқушылар кітаптан есептер шығарады		Кітап Дәптер
Сабақтың соңы. 5мин Рефлекция Бағалау	Оқушылар сабақ соңында келесі сөйлемдерді толықтырады Бүгін сабақта мен.....үйрендім Бүгін сабақта маған....ұнады Бүгін сабақта мен.....қайталадым Бүгін сабақта мен өзіме....деген баға қойдым Үй тапсырмасы №	Оқушылар стикерлерге өз ойларын жазады.	тапсырмалар бойынша 10 балл	Дәптер Стикерлер

---

Мағынаны тану: түртіп алу әдісі/Оқушылар оқулықтағы тақырыпты пайдаланып квадрат теңсіздіктерді шешеді,қиындық келтіретін ұғымдарды белгілеп түсінбеген сұрақтарына сыныптастарынан,мұғалімнен көмек алып білімдерін толықтырады/. 2.тапсырма. 1. 2х2-5х-3≥ 0 д>0, а>0 Шешімі: 2 .5х2-8х+20<0 д<0, а>0 Шешімі жоқ. 3. - х2+3х+4>0 д>0 а<0 Шешімі: Дескриптор 1. квадрат теңсіздіктердің 1-ші коэффициенттің таңбасын анықтайды 2. квадрат теңсіздіктердің дискриминант табады 3. квадрат теңсіздіктердің түбірлерін табады 4. квадрат теңсіздіктердің графигін салады Бағдаршамдар Графиктік сызбалар

5. квадрат теңсіздіктердің шешімін жазады Қалыптастырушы бағалау: «БББ» кестесі бойынша. Кері байланыс: Мұғалім-оқушыға

Білемін Білгім келеді Білдім Жұптық жұмыс. «Кестемен жұмыс» әдісі /Кестедедегі квадрат теңсіздіктерді ажыратады./ 3. тапсырма. Семантикалық карта

Теңсіздік Квадрат теңсіздік 5х-3≥ 0 х2-5х-7≥ 0 2х2-х-3< 0 3х2-5х-3= 0 х-7≥ 0 9х2-3≥ 0 х(х-3) ≥ 0 Дескриптор 1. квадрат теңсіздікті ажырата алады 2. Кейбір теңсіздікті квадарт теңсіздікке келтіре алады Қалыптастырушы бағалау:Қате түсінікті тексеру Кері байланыс:оқушы-оқушыға Топтық жұмыс. «Ойлан,жұптас,бөліс» әдісі 4. тапсырма. Берілген теңсіздіктердің шешімін табыңыз 1. -х2-3х-2≥ 0 д>0, а<0 Шешімі: 2. 9х2-6х+1≤0 д=0 а>0 Шешімі: 3. - х2+4х-4≤0 д=0, а<0 Шешімі: 4. -х2+6х-11>0 д<0, а<0 Шешімі жоқ Дескриптор -Дискриминанттың оң,теріс,о-ге тең болғандағы мәндері бойынша квадрат теңдеудің түбірлерінің санын ажыратады -х-тің мәндері арқылы графигін салады. -графикті пайдаланып квадрат теңсіздіктің шешімдері жатқан аралықты белгілейді . -Белгіленген аралық арқылы квадрат теңсіздіктің шешімін жазады Қалыптастырушы бағалау: Бағдаршам әдісі Жасыл карточка көтерген оқушылар барлығын түсінді. -Не түсіндіңіз? Сары және қызыл карточка көтерген оқушылар:толық түсінбеді. Сіздерге не түсініксіз? білу. Кері байланыс: мұғалім-оқушыға Жеке жұмыс. Деңгейлік тапсырма: 5. тапсырма 1. -3х2-х-7≥ 0 2. -2х2+х-11>0 3. √????2−????−42????−11<0 Маркерлер

4. х2+6х-11>0 Дескриптор: 1.Теңсіздіктің екі жағын да квадраттайды. 2. Теңсіздіктің анықталу облысын табады. 3.Прапорцияның негізгі қасиетін пайдаланады. 4.Шыққан теңсіздікті шешеді. 5.Түбірлерін табады. 6.Түбірлерін сан аралықта белгілейді. 7. Квадрат теңсіздік көмегімен түбірі бар өрнектің мағынасын анықтайды. Қалыптастырушы бағалау:Температураны өлшеу/Не істеп жатырмыз сұрағына жауап арқылы тапсырманың қалай орындалып жатқанын біледі/ Кері байланыс:мұғалім-оқушыға Оқушылардың өзін-өзі бағалауға. Өзіндік жұмыс 6. тапсырма /Теңсіздіктің шешімін табыңыз/ 1.х2-х-7≥ 0 2.- х2-х-1≤0 3. 6х2-11х-30≤0 4. 2х2+7х-4>0 Қалыптастырушы бағалау:Қол белгісі/Қол белгілері арқылы

---

Квадрат теңсіздікті парабола әдісімен шешуді қарастырдық. Көп жағдайда квадрат теңсіздіктерді шешу үшін интервалдар әдісін қолданған ыңғайлы.

ax² + bx + c ˃ 0 (а ≠ 0) квадрат теңсіздігі берілсін. Бұл теңсіздікті интервалдар әдісімен шешу үшін, алдымен y = ax² + bx + c функциясы графигінің Ох осімен қиылысу нүктелерінің абсциссаларын, яғни функцияның нөлдерін табу керек. ax² + bx + c ˃ 0 (а ≠ 0) функциясының нөлдері деп ax² + bx + c = 0 теңдеуінің түбірлері айтылатыны белгілі.

y = ax² + bx + c функциясының нөлдері х₁ және х_2, (х₁ ˂ х₂ ). Сонымен бірге а ˃ 0 (егер а ˂ 0 болса, онда оны а ˃ 0 жағдайына келтіреміз) деп ұйғарайық.

16- параграфта қарастырылған 1- жағдайдың бірінші пунктіне сәйкес y = ax² + bx + c функциясы х˂ х₁ және х˃ х₂ аралығында оң міндерді, ал х₁ ˂ х ˂ х₂ аралығында теріс мәндерді қабылдайды.

Демек, функцияның нөлдері арқылы сан осінде алынған әрбір интервалда функция таңбасын сақтайды және ол таңба функцияның графигі нөлдерден өткенде өзгереді.

Осы қасиет теңсіздіктреді интервалдар әдісімен шешекенде қоданылады.

Теңсіздіктерді интервалдар әдісімен шешу үшін келесі алгоритм қолданылады:

1. 
   
   берілген теңсіздікті Р(х) ˂ 0, Р(х) ˃ 0, Р(х) ≥ 0, Р(х) ≤ 0 түрлерінің біріне келтіреміз;
   
2. 
   
   теңсіздіктің сол жағын нөлге теңестіріп, шыққан теңдеуді шешеміз, яғни сәйкес функцияның нөлдерін табамыз;
   
3. 
   
   теңдеудің түбірлерінің мәнін сан осіне белгілеп, сан осін интервалдарға бөлеміз;
   
4. 
   
   интервалдың кез келген біреуінде функцияның таңбасын анықтап, осы интервалға анықталған таңбаны қоямыз;
   
5. 
   
   теңдеудің түбірі қайталанбаған немесе тақ рет қайталанған жағдайда қалған интервалдардағы таңбаларды кезекпен қоямыз; ал егер түбір жұп рет қайталанса, осы түбірдің екі жағындағы интервалдардың таңбаларын бірдей етіп аламыз;
   
6. 
   
   таңбасы теңсіздік таңбасына сәйкес интервалдарды жауап ретінде аламыз
   

БЖБ№6 алгебра 3 тоқсан

1)Кестеде мектептегі оқушылардың жастары туралы мәлімет берілген. Кестені пайдаланып мәліметтерді гистограммамен беріңіз.

Жасы	7-9	9-11	11-13	13-15	15-17	17-19
Бала саны	230	260	200	250	290	90

---

2 . Кестеде магазиндегі 90 клиенттің кезекте тҧрып кҥту ҧзақтықтары зерттелді. Төмендегі кҥту ҧзақтықтары кестесін толтырыңыз:

Кҥту ҧзақтығы (????) секунд	Жиілік	Жинақтлған жиілік
0≤ ???? < 60		8
60≤ ???? < 120	16
120≤ ???? < 180		48
180≤ ???? < 240		67
240≤ ???? < 300	23

3. Кестеде 20 кҥнде сабаққа келмеген оқушылардың саны кӛрсетілген.

Келмеген оқушылар саны	0	1	2	3	4	5
Кҥндердің саны	4	5	4	3	2	2

Егер стандартты ауытқу 1,5-тен кіші болса, онда қалыпты жағдай болып саналады. Кестедегі берілгендерді пайдаланып, табыңыз:

а) дисперсияны;

b) стандартты ауытқуды;

с) кестедегі берілген жағдай қалыпты бола ма?

2 нуска БЖБ№6 алгебра 3 тоқсан

1. Кестеде мектептегі оқушылардың жастары туралы мәлімет берілген. Кестені пайдаланып мәліметтерді гистограммамен беріңіз.

Жасы	7-9	9-11	11-13	13-15	15-17	17-19
Бала саны	250	290	220	210	260	80

---

[2]

2 . Кестеде магазиндегі 85 клиенттің кезекте тҧрып кҥту ҧзақтықтары зерттелді. Тӛмендегі кҥту ҧзақтықтары кестесін толтырыңыз:

Кҥту ҧзақтығы (????) секунд	Жиілік	Жинақтлған жиілік
0≤ ???? < 60		9
60≤ ???? < 120	14
120≤ ???? < 180		38
180≤ ???? < 240		59
240≤ ???? < 300	26

3. Кестеде сыныптағы 24 оқушының бақылау жҧмысындағы берілген 5 тапсырманың қаншасын

орындағаны туралы саны кӛрсетілген.

Бақылау жҧмысындаағы тапсырмалар саны	5	4	3	2	1	0
Оқушы саны	3	8	5	4	2	2

Егер стандартты ауытқу 1,5-тен кіші болса, онда қалыпты жағдай болып саналады.

Кестедегі

берілгендерді пайдаланып, табыңыз:

а) дисперсияны;

b) стандартты ауытқуды;

с) кестедегі берілген жағдай қалыпты бола ма?0>0>0>0>0>0>

---

Смотрите также файлы

• Инструкция по технике безопасности при прохождении практики на.docx

• Конспект урока функциональной грамотности 5 класс Тема урока Здоровье Элементы структуры урока повторения Особенности реализации.pdf

• Интеграция урочной и внеурочной деятельности по информатике в условиях реализации фгос ооо.docx

• 43. Правила определения подследственности уголовных дел.docx

• Примеры Ученик решаетзадачу. У лошади четыре.doc