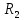Файл: Первое высшее техническое учебное заведение россии министерство науки и высшего образования российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования санктпетербургский горный университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ
Кафедра общей и технической физики
Отчёт
Тема работы: Измерение скорости пули с помощью баллистического маятника
Выполнил: студент гр. НБС-22 Чигинев В.В.
(шифр группы) (подпись) (Ф.И.О.)
Оценка:
Дата:
Проверил
руководитель работы:
(должность) (подпись) (Ф.И.О)
1).Цель работы:
Определить скорость полета пули с помощью крутильных колебаний баллистического маятника.
2). Краткое теоретическое содержание:
Явления, изучаемые в работе: Неупругие соударения, колебания.
Схема установки: Пояснение к схеме:
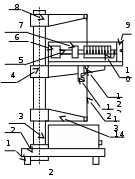 1 – основание;
1 – основание;2 – регулирующие ножки;
3 – колонка;
4, 8, 14 – кронштейны;
9 – стреляющее устройство;
10 – угловая шкала;
12 – фотоэлектрический датчик;
13– проволока;
6 – мисочки с пластилином;
7 – перемещаемые грузы;
5 – стержень;
11 –«водилка»
Скорость полета пули может достигать значительной величины в зависимости от стреляющего устройства. Ее прямое измерение, то есть определение времени, за которое пуля проходит известное расстояние, в учебной лаборатории не представляется возможным.
Для лабораторной работы разработана методика косвенного измерения скорости полета пули с помощью баллистического маятника.
В основе эксперимента лежит явление неупругого соударения тел, в результате которого баллистический маятник совершает крутильные колебания.
Если летящая пуля испытывает неупругий
удар с неподвижным телом большей массы, то скорость тела после удара будет существенно меньше первоначальной скорости пули и ее можно будет измерить достаточно простыми методами.
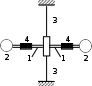
Рисунок 4.1. Баллистический маятник. 1 – стержни, 2 шт.; 2 – емкости с пластилином, 2 шт.; 3 – проволока;
4 – грузы.
Баллистическиймаятникпредставляет собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис. 4.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси, совершая крутильные колебания.
При выводе расчётных формул использованы формулы для момента инерции и периода крутильных колебаний физического маятника, а также законы сохранения момента импульса и полной механической энергии. Принято допущение при этом о малости неконсервативных сил.
На основании закона сохранения момента импульса можно написать
ml (J ml2 )
(4.1)
где m - масса пули; - величина скорости пули; l - расстояние от оси вращения маятника до точки удара пули; - величина угловой скорости маятника; J- момент инерции маятника.
Согласно закону сохранения полной механической энергии при повороте маятника кинетическая энергия маятника переходит в потенциальную энергию закручивающейся проволоки
1 J ml2 2 1 D2
, (4.2)
2 2 max
где max - наибольший угол поворота маятника; D- модуль кручения
Учитывая, что момент инерции пули ml2 существенно меньше момента инерции маятника J, из уравнений (1) и (2) получим

max
2 D2 J/(m2l2 ) . (4.3)
Модуль кручения проволоки Dможно определить, измерив период крутильных колебаний маятника Т.
При малых углах отклонения период крутильных колебаний маятника определяется по формуле
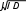 T 2
T 2Модуль кручения проволоки
42 J
(4.4)
D (4.5)
T2
Подставив выражение (4.5) в уравнение (4.3), выразим величину скорости пули
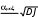 = 2
= 2ml T
J

ml max
(4.6)
Чтобы исключить измерения момента инерции J, запишем периоды колебаний маятника
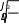 Т1 и Т2 при различных положениях грузов R1 и R2:
Т1 и Т2 при различных положениях грузов R1 и R2:отсюда
T1 2
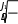 J T2
J T2T2 2
(4.7)
1 1
(4.8)


T
J
2
2 2
В силу того, что момент инерции величина аддитивная, момент инерции баллистического маятника с грузами выразим в виде суммы

0
J J 2MR2 (4.9)
где М- масса одного неподвижного груза; R- расстояние от центра масс груза до оси вращения; J0 - момент инерции маятника без грузов.
Для различных положений грузов на расстояниях R1и R2:
в первом положении
J1 J0
-
2MR2 ; во втором положении

1
J2 J0
-
2MR2

2
Разность моментов инерции
J J 2M(R2 R2 )
Решая уравнение (8) и (10) относительно J1найдем
2M(R2 R2 )T2
J 1 2 1
1 T2 T2
(4.11)
1 2
Подставив в формулу (4.6) период T1 и момент инерции J1 для положения грузов на расстоянии R1, получим окончательную формулу для расчета величины скорости
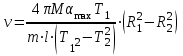
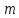 – масса пули, [кг];
– масса пули, [кг]; 
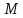 – масса груза, [кг];
– масса груза, [кг]; 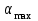 - наибольший угол поворота маятника, [рад];
- наибольший угол поворота маятника, [рад]; 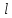 – расстояние от оси вращения маятника до точки удара пули, [м];
– расстояние от оси вращения маятника до точки удара пули, [м];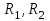 - расстояние от оси вращения до центра масс, [м];
- расстояние от оси вращения до центра масс, [м]; 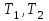 - периоды колебаний в положении R1 и R2 соответственно, [с].
- периоды колебаний в положении R1 и R2 соответственно, [с].3) Основные расчетные формулы:
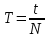 , где
, где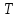 – период колебаний, с;
– период колебаний, с; 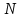 – количество колебаний; t – общее время колебаний. с
– количество колебаний; t – общее время колебаний. с
 – масса пули, кг;
– масса пули, кг; 
 – масса неподвижного груза, кг;
– масса неподвижного груза, кг;  - наибольший угол поворота маятника, рад;
- наибольший угол поворота маятника, рад;  – расстояние от оси вращения маятника до точки удара пули, м;
– расстояние от оси вращения маятника до точки удара пули, м; - расстояние от оси вращения до центра масс, м;
- расстояние от оси вращения до центра масс, м;  - периоды колебаний в положении R1 и R2 соответственно, с.
- периоды колебаний в положении R1 и R2 соответственно, с.4) Расчёт погрешностей:
Косвенная погрешность измерения периода колебаний:
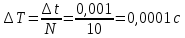 , где ∆t – приборная погрешность секундомера, а N – количество опытов.
, где ∆t – приборная погрешность секундомера, а N – количество опытов.Формула расчёта абсолютной погрешности косвенных измерений скорости пули с помощью баллистического маятника:
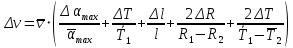
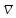 – средняя скорость пули, м/c
– средняя скорость пули, м/c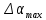 – приборная погрешность угловой шкалы, рад
– приборная погрешность угловой шкалы, рад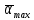 – среднее значение наибольшего угла поворота маятника, рад
– среднее значение наибольшего угла поворота маятника, рад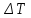 – косвенная погрешность измерений периода колебаний, с
– косвенная погрешность измерений периода колебаний, с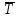 - среднее значение периода колебаний на расстоянии
- среднее значение периода колебаний на расстоянии 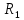 , м
, м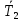 – среднее значение периода колебаний на расстоянии
– среднее значение периода колебаний на расстоянии