Содержание

Введение	3
1 Теоретические аспекты использования дисперсионного анализа в управленческой практике	5
1.1 Понятие и значение дисперсионного анализа	5
1.2 Методы дисперсионного анализа	7
2 Анализ управленческих данных средствами дисперсионного анализа с использованием пакета MS Excel	18
2.1 Инструменты пакета дисперсионного анализа в Microsoft Excel	18
2.2 Проект решения управленческой задачи средствами дисперсионного анализа в пакете Microsoft Excel	22
Заключение	27
Библиографический список	28

Введение

Когда генеральные совокупности распределены нормально и имеют одинаковую, хотя и неизвестную, дисперсию; математические ожидания также неизвестны и могут быть различными, тогда требуется при заданном уровне значимости по выборочным средним проверить нулевую гипотезу о равенстве всех математических ожиданий. Другими словами, требуется установить, значимо или незначимо различаются выборочные средние. Казалось бы, для сравнения нескольких средних можно сравнить их попарно. Однако с возрастанием числа средних возрастает и наибольшее различие между ними: среднее новой выборки может оказаться больше наибольшего или меньше наименьшего из средних, полученных до нового опыта. По этой причине для сравнения нескольких средних пользуются другим методом, который основан на сравнении дисперсий и поэтому назван дисперсионным анализом.

Актуальность данной работы обусловлена тем, что в современном обществе методы дисперсионного анализа применяются повсеместно, принося существенную экономическую выгоду и предупреждая финансовые крахи. Они позволяют принимать разнообразные управленческие решения в условиях риска и неопределенности.

---

Цель данной работы заключается в исследовании возможностей использования дисперсионного анализа в управленческой практике с помощью табличного процессора Microsoft Ехсеl.

Электронные таблицы Microsoft Ехсеl имеют огромный набор возможностей. Однако обычно пользователь в своей работе применяет только их небольшую часть. Происходит это не только от незнания, но и от отсутствия в этом острой необходимости. И действительно, все функции, заложенные в Ехсеl, можно условно разделить на те, знание которых просто необходимо знать, и те, изучать которые можно по мере надобности.

В соответствии с целью исследования были поставлены следующие задачи:

• 
  исследовать теоретические аспекты использования дисперсионного анализа в управленческой практике;
  
• 
  рассмотреть процесс анализа управленческих данных средствами дисперсионного анализа с использованием пакета MS Excel.
  

Объект исследования - дисперсионный анализ.

Предмет исследования – способы использования дисперсионного анализа в управленческой практике.

Основным методом исследования является изучение и анализ специальной литературы по исследуемому вопросу.

В работе были использованы труды следующих авторов: С. Бондаренко, В.И. Борисова, И.К. Васильева, С.В. Глушакова, А.Леоненкова и др.

1 Теоретические аспекты использования дисперсионного анализа в управленческой практике
1.1 Понятие и значение дисперсионного анализа
На практике часто возникает необходимость проверки существенности различия выборочных средних т совокупностей (т>2). Например, требуется оценить влияние различных свойств сырья на показатели качества продукции, плавок на механические свойства металла, количества вносимых удобрений на урожайность, и т.п.

Для эффективного решения такой задачи нужен новый подход, который реализуется в дисперсионном анализе.

Основной целью дисперсионного анализа является исследование значимости различия между средними. Если просто сравниваются средние, в двух выборках, дисперсионный анализ даст тот же результат, что, и обычный t-критерий. Для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий. Для зависимых выборок (если сравниваются две переменные на одном. И том же множестве объектов или наблюдений) [7, С. 72].

---

Фундаментальная концепция дисперсионного анализа предложена английским математиком - статистиком Р.А. Фишером. Для обработки результатов агрономических опытов по выявлению условий получения максимального урожая различных сортов сельскохозяйственных культур в 1918 году. Возможно, более естественным был бы термин анализ суммы квадратов или анализ вариации. Но, в силу традиции употребляется термин дисперсионный анализ. Сам термин «дисперсионный анализ» Фишер употребил позднее [7, С. 73]. По числу факторов, влияние которых исследуется, различают однофакторный. И многофакторный дисперсионный анализ.

Фактор (factors) - категориальная независимая переменная. Чтобы использовать дисперсионный анализ, независимые переменные должны все быть категориальными (неметрическими). Конкретная комбинация уровней факторов называется факторным экспериментам (условиями испытаний) (treatment).

Факторный эксперимент (условия испытаний) (treatment). В дисперсионном анализе конкретная комбинация категорий (уровней) факторов.

Однофакторный дисперсионный анализ (one-way analysis of variance) – метод дисперсионного анализа, при котором используется только один фактор. Однофакторный дисперсионный анализ включает только одну категориальную переменную или единственный фактор. Если существует два или больше факторов, то анализ называют многофакторным дисперсионным анализом. Многофакторный дисперсионный анализ (n-way analysis of variance) – модель дисперсионного анализа. Которая включает два или больше факторов. Взаимосвязь дисперсионного анализа. С t-критерием, другими методами анализа, такими как регрессионный анализ, показана на рис. 1.1 [13, С. 80].



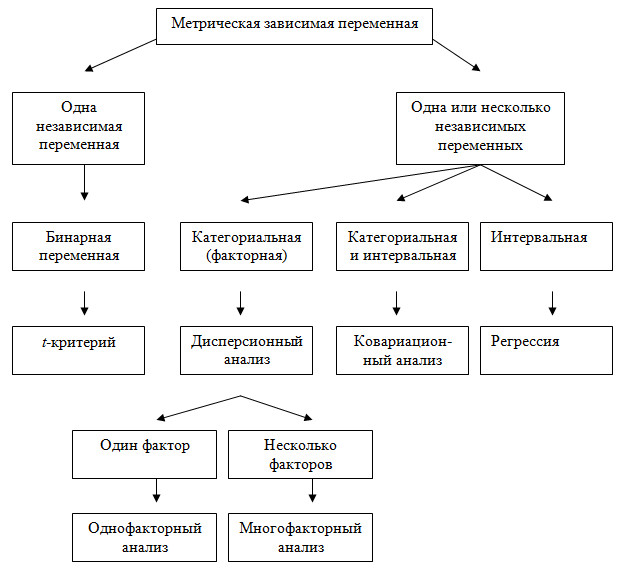
Рисунок 1.1 - Взаимосвязь между t-критерием, дисперсионным и ковариационным анализом и регрессией

Во всех представленных методах анализа (рис. 1.1) используется метрическая зависимая переменная. Дисперсионный и ковариационный анализ может включать несколько независимых переменных (степень использования продукта, лояльность к торговой марке, отношение, важность). Более того, одна из независимых переменных должна быть категориальной и категориальные переменные могут иметь больше двух уровней. С другой стороны, t-критерий предназначен для использования в случае с единственной бинарной независимой переменной. Например, различие в предпочтениях товара у лояльных и нелояльных респондентов можно узнать, выполнив проверку с помощью t-критерия. Регрессионный анализ, подобный дисперсионному и ковариационному, также может включать несколько независимых переменных. Однако все независимые переменные, в основном, измеряются интервальной шкалой, хотя бинарные или категориальные переменные могут приспосабливаться к анализу за счет введения фиктивных (dummy) переменных.

---

Итак, в настоящее время дисперсионный анализ определяется как статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, а также для последующего планирования аналогичных экспериментов.
1.2 Методы дисперсионного анализа
При проведении экономического анализа часто необходимо оценить влияние на целевую функцию y качественного фактора x. _. Таким фактором могут быть, например, партии сырья, отрасли промышленности, регионы и т.д.

На современном этапе выделяются следующие основные методы дисперсионного анализа

1. 
   Метод по Фишеру (Fisher) - критерий F. Данный метод применяется в однофакторном дисперсионном анализе, когда совокупная дисперсия всех наблюдаемых значений раскладывается на дисперсию внутри отдельных групп и дисперсию между группами.
   
2. 
   Метод «общей линейной модели», в его основе лежит корреляционный или регрессионный анализ, применяемый в многофакторном анализе.
   

Однофакторная дисперсионная модель имеет вид:

x_ij = μ + F_j + ε_ij, (1.1)


где х_ij – значение исследуемой переменой, полученной на i-м уровне фактора (i=1,2,...,т) c j-м порядковым номером (j=1,2,...,n);

F_i – эффект, обусловленный влиянием i-го уровня фактора;

ε_ij – случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменой внутри отдельного уровня.

Простейшим случаем дисперсионного анализа является одномерный однофакторный анализ для двух или нескольких независимых групп, когда все группы объединены по одному признаку.

В ходе анализа проверяется нулевая гипотеза о равенстве средних. При анализе двух групп дисперсионный анализ тождественен двухвыборочному t-критерию Стьюдента для независимых выборок, и величина F-статистики равна квадрату соответствующей t-статистики.

Для подтверждения положения о равенстве дисперсий обычно применяется критерий Ливена (Levene's test). В случае отвержения гипотезы о равенстве дисперсий основной анализ неприменим. Если дисперсии равны, то для оценки соотношения межгрупповой и внутригрупповой изменчивости применяется F-критерий Фишера.Если F-статистика превышает критическое значение, то нулевая гипотеза отвергается и делается вывод о неравенстве средних. При анализе средних двух групп результаты могут быть интерпретированы непосредственно после применения критерия Фишера.

---

Пусть данные о влиянии некоторого качественного фактора на количественный в форме таблицы 1.1 [13, С. 81].
Таблица 1.1 - Влияние качественного фактора на исследуемый показатель



Модель зависимости значений 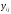от фактора столбцов можно представить в следующем виде:

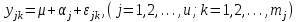(1.1)

где 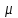- общее среднее,

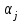-отклонение от общего среднего для j-го уровня фактора,

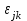- случайная составляющая.

По выборочным данным можно вычислить:

1. 
   среднее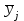 для каждого уровня фактора (среднее по столбцам) x_j (j=1,2,...u ), по m_j параллельным опытам, где m_j – число данных в столбце j:
   

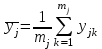(1.2)

2. 
   общее среднее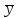 по всем N опытам, т.е. по всем m_j параллельным опытам на всех уровнях фактора x_j ( ):
   

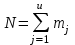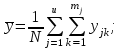(1.3)

3. 
   общую сумму квадратов отклонений Q₀:
   

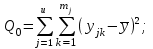(1.4)

3. 
   сумму квадратов, характеризующую влияние фактора x (отклонения между группами)
   

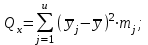; (1.5)

3. 
   остаточную сумму квадратов, зависящую от ошибки  (отклонения внутри групп)
   

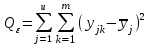(1.6)

Тождество дисперсионного анализа имеет вид:

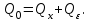(1.7)

На основании вычисленных сумм квадратов вычисляются:

1. 
   оценка дисперсии относительно общего среднего :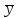
   

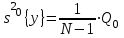(1.8)

где

---

Смотрите также файлы

• Реферат (Мектептегі гимнастика сабаыны дістемесі ) Тексерген Тугельбаев Ерик Нурмаханбетович.docx

• Программа курса английского языка Английский с удовольствием ("Enjoy English") для учащихся.doc

• Методика составления комплексов производственной гимнастики.docx

• Сздік (словарь).docx

• 9сынып аза тілі 4тосан 202021 4тосан бойынша жиынты баалауа арналан тапсырмалар.doc