Файл: 1 Теоретические аспекты использования дисперсионного анализа в управленческой практике.docx
Добавлен: 12.01.2024
Просмотров: 109
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- число степеней свободы;
2) оценка дисперсии «между группами», определяемыми уровнями xj:
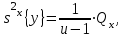 (1.9)
(1.9)
где число степеней свободы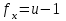 .
.
3) выборочная оценка дисперсии «внутри групп», вычисляемая как средняя оценка по всем u группам:
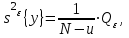 (1.10)
(1.10)
с числом степеней свободы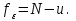
Числа степеней свободы должны удовлетворять соотношению
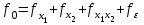 (1.11)
(1.11)
Для того, чтобы сделать вывод о том, влияет ли на исследуемые показатели качественный фактор, сопоставляют дисперсию между группами с общей дисперсией. При этом выдвигают следующие гипотезы [18, С. 315]:
H0: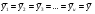 , т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.
H1: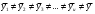 , , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.
Оценивание значимости влияния фактора x выполняется по F-критерию Фишера, для чего формируется следующее F-отношение:
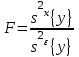 . (1.12)
. (1.12)
Фактор x признается незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости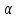 и числа степеней свободы сравниваемых дисперсий
и числа степеней свободы сравниваемых дисперсий 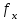 и
и 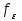 .
.
Табличное значение критерия Фишера определяется дл числа степеней свободы u-1 и N-1 и вероятности ошибки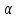
.
Т.е если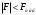 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
Если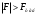 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
Результаты дисперсионного анализа сводятся в таблицу 1.2 [18, С. 316].

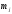 - число данных в столбце, u- число столбцов, m – число строк.
- число данных в столбце, u- число столбцов, m – число строк.
Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию двух одновременно действующих факторов x1 и x2 . Такими факторами могут быть, например, форма собственности предприятия x1 и вид экономической деятельности x2.
Модель двухфакторного дисперсионного анализа имеет вид:
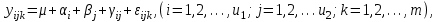 (1.13)
(1.13)
где - общее среднее,
- общее среднее, 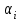 -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1,
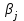 - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2,
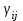 - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов, 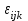 - случайная составляющая.
- случайная составляющая.
В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы:
В этом случае по выборочным значениям вычисляются:
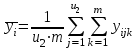 (1.14)
(1.14)
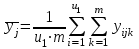 (1.15)
(1.15)
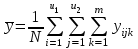 (1.16)
(1.16)
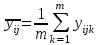 . (1.17)
. (1.17)
В таблице 1.3 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках [18, С. 320].
Таблица 1.3 - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
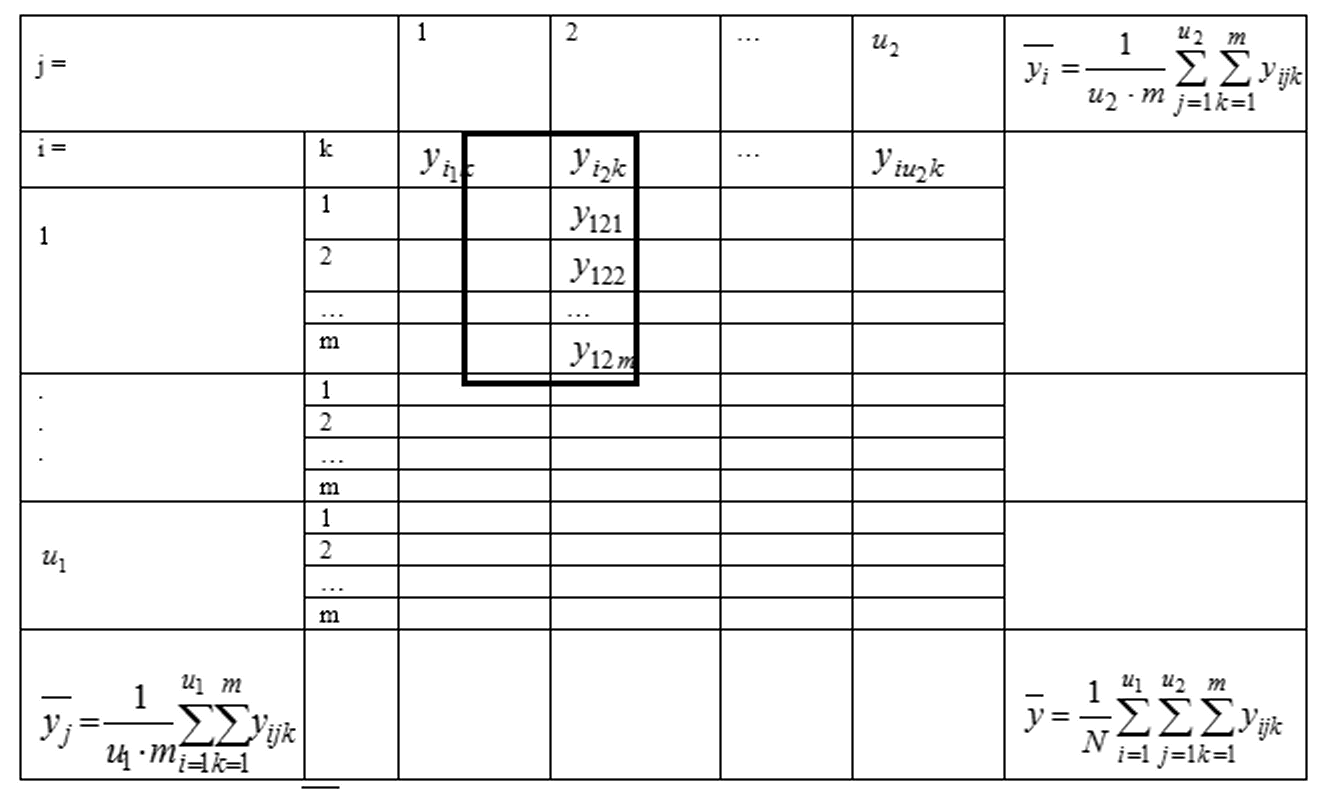
В табл. 1.3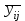
 вычисляется по выделенной части столбца, содержащей m параллельных опытов.
вычисляется по выделенной части столбца, содержащей m параллельных опытов.
Общая сумма квадратов отклонений Q0 рассчитывается по формуле:
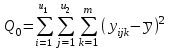 (1.17)
(1.17)
Эту сумму можно разложить на 4 составляющие:
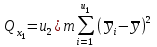 (1.18)
(1.18)
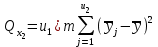 (1.19)
(1.19)
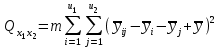 (1.20)
(1.20)
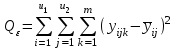 (1.21)
(1.21)
Указанные пять сумм, поделенные на соответствующее число степеней свободы, дают пять различных оценок дисперсии, если влияние факторов x1 и x2 незначимо. Для проведения дисперсионного анализа вычисляются следующие дисперсии:
 (1.22)
(1.22)
где -общее число наблюдений, а число степеней свободы
-общее число наблюдений, а число степеней свободы
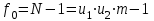 (1.23)
(1.23)
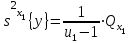 (1.24)
(1.24)
где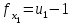 - число степеней свободы.
- число степеней свободы.
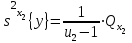 (1.25)
(1.25)
где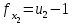 - число степеней свободы;
- число степеней свободы;
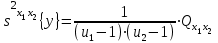 (1.26)
(1.26)
с числом степеней свободы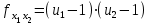 ;
;
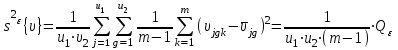 (1.27)
(1.27)
с числом степеней свободы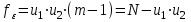 .
.
Числа степеней свободы должны удовлетворять соотношению
 (1.28)
(1.28)
Статистическое оценивание значимости влияния факторов x1 , x2 и взаимодействия x1x2 выполняются по F-критерию Фишера, для чего формируются следующие F-отношения:
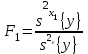 ,
, 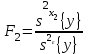 ,
, 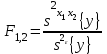 (1.29)
(1.29)
Фактор x1 или x2 , или взаимодействие x1x2 признаются незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости и числа степеней свободы сравниваемых дисперсий.
и числа степеней свободы сравниваемых дисперсий.
Для того, чтобы сделать вывод о том, влияют ли на исследуемые показатели качественные факторы, выдвигают следующие гипотезы:
H0: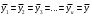
, т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
H1: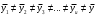 , т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
, т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
H0: , т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
H1: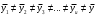 , , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
H0: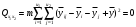 , т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо.
, т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо.
H1: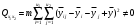 , фактор взаимодействия значим..
, фактор взаимодействия значим..
Если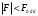 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
Если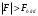 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
Результаты двухфакторного дисперсионного анализа представляются в виде таблице 1.4 [18, С. 321].
Таблица 1.4 - Двухфакторный дисперсионный анализ при равном числе наблюдений в ячейках

где m – число данных в строке (число повторов в ячейке),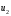 - число столбцов,
- число столбцов, 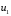 - число строк.
- число строк.
В заключении необходимо отметить, что существуют условия применения дисперсионного анализа:
2) оценка дисперсии «между группами», определяемыми уровнями xj:
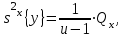 (1.9)
(1.9)где число степеней свободы
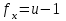 .
.3) выборочная оценка дисперсии «внутри групп», вычисляемая как средняя оценка по всем u группам:
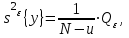 (1.10)
(1.10)с числом степеней свободы
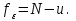
Числа степеней свободы должны удовлетворять соотношению
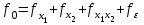 (1.11)
(1.11)Для того, чтобы сделать вывод о том, влияет ли на исследуемые показатели качественный фактор, сопоставляют дисперсию между группами с общей дисперсией. При этом выдвигают следующие гипотезы [18, С. 315]:
H0:
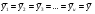 , т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.H1:
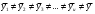 , , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.Оценивание значимости влияния фактора x выполняется по F-критерию Фишера, для чего формируется следующее F-отношение:
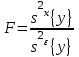 . (1.12)
. (1.12)Фактор x признается незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости
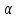 и числа степеней свободы сравниваемых дисперсий
и числа степеней свободы сравниваемых дисперсий 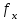 и
и 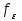 .
.Табличное значение критерия Фишера определяется дл числа степеней свободы u-1 и N-1 и вероятности ошибки
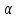
.
Т.е если
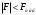 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.Если
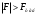 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.Результаты дисперсионного анализа сводятся в таблицу 1.2 [18, С. 316].
Таблица 1.2 - Однофакторный дисперсионный анализ

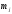 - число данных в столбце, u- число столбцов, m – число строк.
- число данных в столбце, u- число столбцов, m – число строк.Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию двух одновременно действующих факторов x1 и x2 . Такими факторами могут быть, например, форма собственности предприятия x1 и вид экономической деятельности x2.
Модель двухфакторного дисперсионного анализа имеет вид:
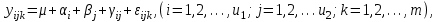 (1.13)
(1.13)где
 - общее среднее,
- общее среднее, 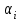 -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1, 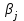 - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2, 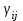 - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов, 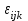 - случайная составляющая.
- случайная составляющая.В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы:
-
Qx1-по фактору x1, -
Qx2-по фактору x2, -
Q-остаточную сумму квадратов, зависящую от ошибки , -
Q x1x2-зависящую от взаимодействия (произведения) x1x2 двух факторов.
В этом случае по выборочным значениям вычисляются:
-
среднее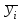 для каждого уровня фактора x1:
для каждого уровня фактора x1:
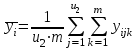 (1.14)
(1.14)-
среднее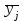 для каждого уровня фактора x2:
для каждого уровня фактора x2:
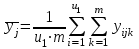 (1.15)
(1.15)-
общее среднее по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (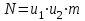 ):
):
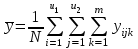 (1.16)
(1.16)-
среднее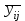 по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
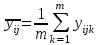 . (1.17)
. (1.17)В таблице 1.3 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках [18, С. 320].
Таблица 1.3 - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе

В табл. 1.3
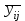
 вычисляется по выделенной части столбца, содержащей m параллельных опытов.
вычисляется по выделенной части столбца, содержащей m параллельных опытов.Общая сумма квадратов отклонений Q0 рассчитывается по формуле:
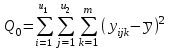 (1.17)
(1.17)Эту сумму можно разложить на 4 составляющие:
-
сумму, характеризующую влияние фактора x1:
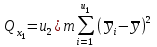 (1.18)
(1.18)-
сумму, характеризующую влияние фактора x2:
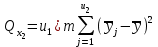 (1.19)
(1.19)-
сумму, характеризующую результат влияния взаимодействия x1x2:
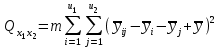 (1.20)
(1.20)-
сумму, характеризующую влияние ошибки :
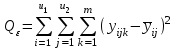 (1.21)
(1.21)Указанные пять сумм, поделенные на соответствующее число степеней свободы, дают пять различных оценок дисперсии, если влияние факторов x1 и x2 незначимо. Для проведения дисперсионного анализа вычисляются следующие дисперсии:
-
оценка дисперсии относительно общего среднего :
:
 (1.22)
(1.22)где
 -общее число наблюдений, а число степеней свободы
-общее число наблюдений, а число степеней свободы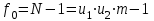 (1.23)
(1.23)-
оценка дисперсии «между строками», определяемыми уровнями x1j:
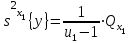 (1.24)
(1.24)где
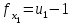 - число степеней свободы.
- число степеней свободы.-
оценка дисперсии «между столбцами», соответствующими уровням фактора x2:
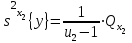 (1.25)
(1.25)где
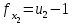 - число степеней свободы;
- число степеней свободы;-
оценка дисперсии «между сериями» по m параллельным опытам каждая
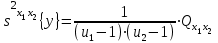 (1.26)
(1.26)с числом степеней свободы
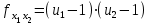 ;
;-
оценка дисперсии «внутри серий» по m параллельным опытам, вычисляемая как средняя оценка по всем u1u2 сериям:
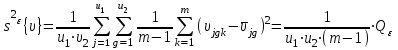 (1.27)
(1.27)с числом степеней свободы
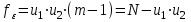 .
.Числа степеней свободы должны удовлетворять соотношению
 (1.28)
(1.28)Статистическое оценивание значимости влияния факторов x1 , x2 и взаимодействия x1x2 выполняются по F-критерию Фишера, для чего формируются следующие F-отношения:
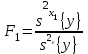 ,
, 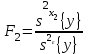 ,
, 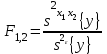 (1.29)
(1.29)Фактор x1 или x2 , или взаимодействие x1x2 признаются незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости
 и числа степеней свободы сравниваемых дисперсий.
и числа степеней свободы сравниваемых дисперсий.Для того, чтобы сделать вывод о том, влияют ли на исследуемые показатели качественные факторы, выдвигают следующие гипотезы:
H0:
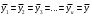
, т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
H1:
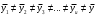 , т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
, т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.H0:
 , т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.H1:
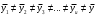 , , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.H0:
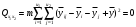 , т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо.
, т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо.H1:
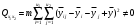 , фактор взаимодействия значим..
, фактор взаимодействия значим..Если
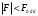 , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.Если
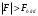 , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.Результаты двухфакторного дисперсионного анализа представляются в виде таблице 1.4 [18, С. 321].
Таблица 1.4 - Двухфакторный дисперсионный анализ при равном числе наблюдений в ячейках

где m – число данных в строке (число повторов в ячейке),
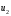 - число столбцов,
- число столбцов, 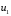 - число строк.
- число строк.В заключении необходимо отметить, что существуют условия применения дисперсионного анализа:
-
Задачей исследования является определение силы влияния одного (до 3) факторов на результат или определение силы совместного влияния различных факторов (пол и возраст, физическая активность и питание и т.д.). -
Изучаемые факторы должны быть независимые (несвязанные) между собой. Например, нельзя изучать совместное влияние стажа работы и возраста, роста и веса детей и т.д. на заболеваемость населения. -
Подбор групп для исследования проводится рандомизированно (случайный отбор). Организация дисперсионного комплекса с выполнением принципа случайности отбора вариантов называется рандомизацией (перев. с англ. - random), т.е. выбранные наугад. -
Можно применять как количественные, так и качественные (атрибутивные) признаки.