Файл: Обработка и анализ статистических данных о выездах пожарных подразделений по вызовам в городе.docx
Добавлен: 12.01.2024
Просмотров: 260
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
j-ого интервала.
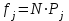
Проведем необходимые вычисления теоретической частоты
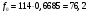
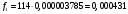
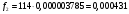
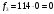
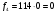
Визуальное сопоставление интервальных вариационных рядов эмпирического и теоретического распределений позволяет сделать вывод о сходстве либо о несходстве характеров распределений. Для того чтобы определить, какими можно считать расхождения между теоретическим и эмпирическим распределениями: случайными (т.е. следствием недостаточного числа наблюдений, использованных для построения эмпирического распределения) или закономерными (т.е. обусловленными неверным выбором теоретического закона распределения), используется статистический критерий согласия Романовского.
Рис. 7. Гистограммы эмпирического и теоретического распределений длительности времени обслуживания вызова пожарными подразделениями в городе
Визуальное сопоставление полигонов эмпирического и теоретического распределений позволяет сделать вывод о сходстве характеров рассматриваемых распределений. Более точное заключение можно сделать, если использовать статистический критерий согласия Романовского:
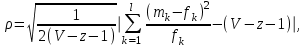
где V- число групп значений случайной величины, для каждой из которых должно выполняться условие fk ≥ 9, если для какой-либо k-ой группы это условие не выполняется, то эта группа объединяется с предыдущей или с последующей группой, а соответствующие им частоты складываются, для нашего примера V=3; z- число параметров закона распределения, для закона Пуассона и для показательного закона z=1.
Если значение критерия Романовского ρ < 3, то расхождения можно считать не существенными (случайными), если ρ ≥ 3 – существенными.
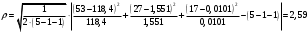
Расчетное значение
ρ=2,59 не превышает значения 3, т.е. расхождения между эмпирическим и теоретическим распределениями можно считать не существенными. Таким образом, закон Пуассона можно использовать для вероятностных расчетов распределения числа вызовов на различных временных интервалах.
Заключение
Если для рассматриваемого примера в состав дежурных караулов городских ПЧ включить 5 пожарных автомобилей, то будет обеспечен весьма высокий уровень противопожарной защиты города: в течение рассматриваемого периода времени (120 суток) для обслуживания вызовов в городе потребуется привлечь дополнительные пожарные автомобили извне лишь в единичных случаях.
Список литературы:
ВИПТШ МВД СССР. – М., 1988. – С. 100 – 107.
ник. – М.: ИНФРА-М, 2009. – 416 с.
лекций для слушателей очной и заочной форм обучения.– М.: Академия ГПСМЧС России, 2008. – 68 с.
318.
при разработке индивидуальных заданий расчетного характера // Материалы 6-й международной конференции "Системы безопасности" – СБ-97. – М.: МИПБ МВД России, 1997. – С. 124 – 125.
2010. – С. 270 – 272.
лекций. – М.: Академия ГПС МЧС России, 2007. – 68 с.
С. 119 – 120.
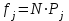
Проведем необходимые вычисления теоретической частоты
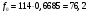
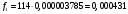
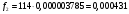
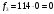
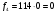
Визуальное сопоставление интервальных вариационных рядов эмпирического и теоретического распределений позволяет сделать вывод о сходстве либо о несходстве характеров распределений. Для того чтобы определить, какими можно считать расхождения между теоретическим и эмпирическим распределениями: случайными (т.е. следствием недостаточного числа наблюдений, использованных для построения эмпирического распределения) или закономерными (т.е. обусловленными неверным выбором теоретического закона распределения), используется статистический критерий согласия Романовского.

Рис. 7. Гистограммы эмпирического и теоретического распределений длительности времени обслуживания вызова пожарными подразделениями в городе
Визуальное сопоставление полигонов эмпирического и теоретического распределений позволяет сделать вывод о сходстве характеров рассматриваемых распределений. Более точное заключение можно сделать, если использовать статистический критерий согласия Романовского:
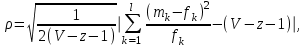
где V- число групп значений случайной величины, для каждой из которых должно выполняться условие fk ≥ 9, если для какой-либо k-ой группы это условие не выполняется, то эта группа объединяется с предыдущей или с последующей группой, а соответствующие им частоты складываются, для нашего примера V=3; z- число параметров закона распределения, для закона Пуассона и для показательного закона z=1.
Если значение критерия Романовского ρ < 3, то расхождения можно считать не существенными (случайными), если ρ ≥ 3 – существенными.
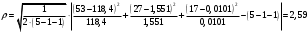
Расчетное значение
ρ=2,59 не превышает значения 3, т.е. расхождения между эмпирическим и теоретическим распределениями можно считать не существенными. Таким образом, закон Пуассона можно использовать для вероятностных расчетов распределения числа вызовов на различных временных интервалах.
Заключение
Если для рассматриваемого примера в состав дежурных караулов городских ПЧ включить 5 пожарных автомобилей, то будет обеспечен весьма высокий уровень противопожарной защиты города: в течение рассматриваемого периода времени (120 суток) для обслуживания вызовов в городе потребуется привлечь дополнительные пожарные автомобили извне лишь в единичных случаях.
Список литературы:
-
Брушлинский Н. Н., Соболев Н. Н. Анализ циклических изменений плотности потока вызовов пожарных подразделений в городе // Организация, тактика и техника тушения пожаров на объектах народного хозяйства: Сб. науч.тр./
ВИПТШ МВД СССР. – М., 1988. – С. 100 – 107.
-
Ефимова М. Р., Петрова Е. В., Румянцев В. Н. Общая теория статистики: Учеб-
ник. – М.: ИНФРА-М, 2009. – 416 с.
-
Организация и управление в области обеспечения пожарной безопасности. Учебное пособие / В. Л. Семиков, В. А. Рязанов, Н. Н. Соболев и др. – М.: Ака-демия ГПС МЧС России, 2009. – 329 с.
-
Соболев Н. Н. Моделирование организационно-управленческих ситуаций: Курс
лекций для слушателей очной и заочной форм обучения.– М.: Академия ГПСМЧС России, 2008. – 68 с.
-
Соболев Н. Н. Интернет-технология формирования индивидуальных учебных заданий и их выполнения // Материалы 22-й научно-технической конференции «Системы безопасности» – СБ-2013. – М.:АГПС МЧС России, 2013. – С. 316 –
318.
-
Соболев Н. Н. Использование компьютерной технологии в учебном процессе
при разработке индивидуальных заданий расчетного характера // Материалы 6-й международной конференции "Системы безопасности" – СБ-97. – М.: МИПБ МВД России, 1997. – С. 124 – 125.
-
Соболев Н. Н. Компьютерная имитационная модель для демонстрации процесса занятости пожарных подразделений обслуживанием вызовов в городе // Мате-риалы 21-й научно-технической конференции «Системы безопасности» – СБ-2012. – М.: АГПС МЧС России, 2012. – С. 168 – 171.
-
Соболев Н. Н. Компьютерная технология формирования индивидуальных рас-четных заданий в учебном процессе // Материалы 19-й научно-технической конференции «Системы безопасности» – СБ-2010. – М.: АГПС МЧС России,
2010. – С. 270 – 272.
-
Соболев Н. Н. Моделирование организационно-управленческих ситуаций: Курс
лекций. – М.: Академия ГПС МЧС России, 2007. – 68 с.
-
Соболев Н. Н., Коломиец Ю. И. Учебный комплекс по обработке статистиче-ских данных и математическому моделированию организационно-управленческих ситуаций в пожарной охране // Материалы 6-й международной конференции "Системы безопасности" – СБ-97. - М.: МИПБ МВД РФ, 1997. –
С. 119 – 120.
-
Соболев Н. Н. Статистические закономерности циклических изменений интен-сивности потока вызовов пожарных подразделений в городах // Материалы 23-й научно-технической конференции «Системы безопасности – 2014». – М.: Акаде-мия ГПС МЧС России, 2014. – С. 192 - 195.
-
Соболев Н. Н. Статистические закономерности циклических изменений часто-сти возникновения пожаров в городах со временем суток // Материалы 24-й на-учно-технической конференции «Системы безопасности – 2015». – М.: Акаде-мия ГПС МЧС России, 2015. – С.