6. 
   Проведем статистическое исследование и моделирование вероятностного распределения числа вызовов пожарных подразделений (ПП) в городе в интервале времени продолжительностью одни сутки.
   

6.1. Период времени наблюдения T_набл за процессом функционирования ПП в городе разбивается на интервалы одинаковой длительности  = 1 сут. Общее число M выделенных временных интервалов определяется по формуле
M = Tнабл/.

Так как длительность периода времени наблюдения для учебного диспетчерского журнала выездов ПП по вызовам в городе составляет Tнабл =120 суток, то число выделенных временных интервалов длительности

• 
  = 1 сут оказывается равным M = 120. На каждом из этих временных интервалов (т.е. в течение каждых суток) происходит то или иное число вызовов ПП, которые зафиксированы в диспетчерском журнале.
  

6.2. По диспетчерскому журналу подсчитывается число m_k интервалов времени (суток) с определенным числом k вызовов (k = 0, 1, 2,..). Подсчеты ведутся исходя из данных, представленных в графе "Время вызова: день". Вызовы, возникающие в течение одних суток, имеют одинаковые даты поступления.

Получаемые в результате подсчетов значения m_k, называемые эмпирическими частотами, связаны между собой соотношением:


mk M .

k 0
Определить значение m₀ непосредственно по диспетчерскому журналу затруднительно, так как для этого нужно подсчитать число суток, даты которых отсутствуют в журнале (в эти дни вызовов не происходило). Исхоя из соотношения, можно расчетным путем определить число m_o временных интервалов (суток), в течение которых не произошло ни одного вызова:

---

	 m2	 m3...).
m0 M  mk M (m1
k 1

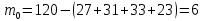
Эмпирическая вероятность _k() (называемая также частостью или относительной частотой) того, что в интервале времени продолжительностью  = 1 сут в городе произойдет определенное число k вызовов, оценивается как доля, которую в общем числе M выделенных временных интервалов (суток) составляют интервалы, в течение каждого из которых произошло ровно k вызовов:

k () 	mk	.
	M

Перечень различных значений k = 0, 1, 2, 3,..., каждому из которых поставлены в соответствие значения эмпирической частоты m_k и эмпирической вероятности _k(), образует дискретный вариационный ряд эмпирического распределения числа вызовов ПП в городе на интервале времени продолжительностью  = 1 сут (табл. 7).
Построим математическую модель, описывающую вероятностные закономерности потока вызовов ПП в городе, в виде закона распределения Пуассона (этот закон принимается в качестве теоретического распределения). Для этой цели произведем оценку параметра  для этого закона, который называется интенсивностью потока вызовов и представляет собой среднее число вызовов ПП в городе за единицу времени (например, за сутки или за час):

 = n / Tнабл (вызовов/ед.времени),

где n – общее число вызовов в диспетчерском журнале за период времени наблюдения T_набл.
Интенсивность потока вызовов ПП в городе, в котором за 365 суток зафиксированы 108 вызовов, оценивается по формуле следующим образом:

---

• 
  = 114 (вызовов) / 365 (сут) = 0,312 (вызова/сут) = 0,0131 (вызова/ч).
  

Таблица 7

---

Эмпирическое и теоретическое (пуассоновское) распределения числа вызовов ПП в интервале времени длительностью 1 сутки в городе

Число		Распределение
	эмпирическое		теоретическое
вызовов k
за время	частота	вероятность	вероятность	частота
 = 1 сут	mk	k ()	pk()	fk
0
	51	0,447	0,9869	118,4
1	36	0,315	0,01292	1,551
2	21	0,184	0,00008468	0,0101
3	6	0,052	0,0000007395	0,00008874
Более 3	-	-	0,00000000726	0,0000008719
Сумма	114	1,0000	1,0000	365,0

---

Проведем ряд расчетов теоретической вероятности














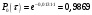
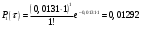
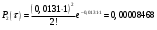
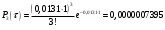
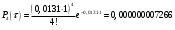
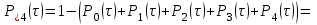
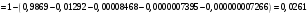
Проведем расчет теоретических частот












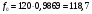
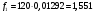
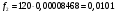
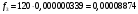
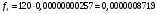
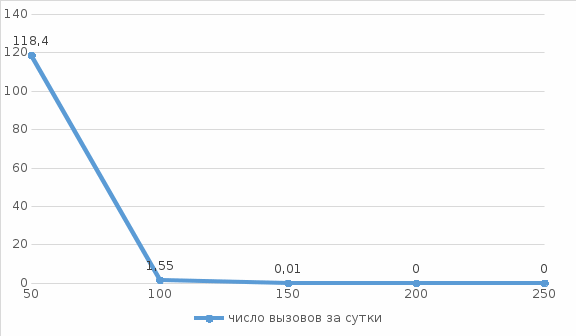
Рис. 6. Полигон частот эмпирического и теоретического распределений числа вызовов пожарных подразделений в городе Бор в интервале времени длительности одни сутки

7. 
   Произведем количественное описание закономерностей изменения интенсивности потока вызовов пожарных подразделений (ПП) в городе под влиянием временных факторов, имеющих циклический характер (период времени суток и месяц года).
   

7.1. Для количественной оценки совместного влияния i-го периода времени суток (i = 1, 2,..., I) и j-го месяца года (j = 1, 2,..., J) на интенсивность потока вызовов ПП в городе производится построение двухфакторной мультипликативной регрессионной модели, которая имеет вид:

ij ai bj,

где  – постоянная составляющая плотности потока вызовов ПП в городе; a_iи b_j–параметры модели,соответственно отражающие эффекты

влияния i-го периода времени суток и j-го месяца;
_ij – рассчитываемое с помощью модели значение плотности потокавызовов в i-й период времени суток j-го месяца.
На основе статистических данных, содержащихся в учебном диспетчерском журнале выездов ПП по вызовам в городе, параметры b_j

---

Смотрите также файлы

• Инструкция Один человек выполняет подтягивания, другие участники ведут счет и время. Далее используя необходимые расчеты, определяют мощность.docx

• Фотосинтез и хемосинтез.doc

• Анамнез 1) Были ли вирусные инфекции (эпид паротит, вирусный гепатит, энтеровирус Коксаки В, инф мононуклеоз, краснуха, ветряная оспа, герпес, цмв, корь, грипп).docx

• Политологи я.ppt

• Педагогика оулы ббк 74. 00 П24.doc