(j = 1, 2,..., J) представляется возможным оценить лишь для четырех месяцев (J = 4), суммарная продолжительность которых составляет период времени наблюдения T_набл = 120 суток = 2880 ч: январь – 31 суток, февраль

– 28 суток, март – 31 суток, апрель – 30 суток.

Таблица 8
Оценки эффектов влияния периодов времени суток на интенсивность потока
вызовов пожарных подразделений в городе

Номер	Период		Длительность	Число	Интенсивность	Эффект
периода	времени		периода	вызовов	потока	Влияния
i	суток, час		Ti,ч/год	mi	λi ,1/ч	ai
1	с 0	до 4	1460	20	0,0143	1,415
2	с 4	до 8	1460	17	0,0089	0,8811
3	с 8 до 12		1460	20	0,0082	0,8118
4	с 12	до 16	1460	18	0,0068	0,673
5	с 16	до 20	1460	14	0,0102	1,0099
6	с 20	до 24	1460	25	0,0123	1,2178
Итого	c 0 до 24		8760	114	0,0101	6,000

---

Таблица 9
Оценки эффектов влияния месяцев года на интенсивность потока

вызовов пожарных подразделений в городе

Номер	Месяц	Длительность	Число	Интенсивность	Эффект
месяца		месяца	вызовов	потока	влияния
	года
j		Tj,ч/год	mj	λj ,1/ч	bj
1	Январь	744	27	0,0362	2,763
2	Февраль	672	31	0,0461	3,519
3	Март	744	33	0,0443	3,381
4	Апрель	720	23	0,0319	2,435
Итого	2020 год	8760	114	0,0131	12,09

---

8. 
   Проведем статистическое исследование и моделирование вероятностного распределения длительности времени обслуживания вызова пожарными подразделениями (ПП) в городе.
   

8.1. Область возможных значений величины _обс длительности времени обслуживания вызова ПП, представляющая собой множество неотрицательных действительных чисел, разбивается на v интервалов. Выделенные интервалы последовательно нумеруются. Интервал, которому присвоен
порядковый номер j (j =1, 2,..., v), задается своими границами: нижней ^н_j и верхней ^в_j .
Выделим v = 5 интервалов со следующими границами: [0; 30), [30; 60), [60; 90), [90; 120), [120; ).
8.2. По результатам наблюдений за длительностью времени обслуживания n вызовов, зафиксированных в диспетчерском журнале, подсчитывается число m_j вызовов, длительность времени обслуживания каждого из которых попадает в j-й интервал (j = 1, 2,..., v), т.е. выполняется условие

• 
  ^н_j _обс< ^в_j . Для полученных в результате подсчетов значений эмпирических частот m_j (j = 1, 2, ..., v) должно выполняться соотношение
  

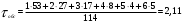
Таблица 10

---

Эмпирическое и теоретическое (показательное) распределения длительности времени обслуживания вызова пожарными подразделениями в городе

Номер	Границы интервала,			Эмпирическое		Теоретическое
		мин		распределение		распределение
интервала
	нj		вj	m j	j	p j	f j
j
1	0		30	27	0,236	0,6582	40,7
							23,8
2	30		60	17	0,149	0,00000358	0,000078
							2,6
3	60		90	8	0,071	0,00000358	0,000078
4	90		120	4	0,035	0	0
5	120			5	0,043	0	0
Всего	-		-	114	1,000	1,000

---

Для определения эмпирического распределения необходимо сделать следующее: по диспетчерскому журналу подсчитать число m_j вызовов, у которых длительность времени обслуживания τ_обсл. попадает в j-й интервал.

Полученные в результате подсчетов значения m_j называются эмпирическими частотами и связаны между собой соотношением:


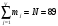
Эмпирическая вероятность ω_j (относительная частота) того, что τ_обсл попадет в j-й интервал, оценивается как доля, которую в общем числе N вызовов составляют вызовы, попавшие в j-й интервал:


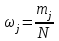
Для определения теоретической вероятности p_j того, что значение τ_обсл окажется меньше или больше какого-либо значения τ или попадет в j-й интервал используем показательное распределение








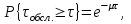
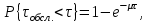
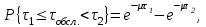
где µ - параметр показательного закона распределения µ=1/τ_{ср.обсл.}.
Средняя длительность времени обслуживания τ_{ср.обсл.} может быть вычислена двумя способами:

1) как среднее арифметическое:



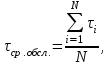
где τ_i – длительность времени обслуживания i-ого вызова, в нашем случае τ_{ср. обсл.} = 2,12 мин
2) как среднее арифметическое взвешенное:



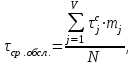
где - середина j-ого интервала, в нашем случае τ_{ср. обсл.}=2,39 мин.
Среднее арифметическое взвешенное является менее точным, чем простое арифметическое, но для его нахождения требуется меньший объем вычислений.
Проведем расчет теоретической вероятности для примерного варианта.












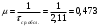
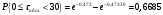
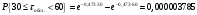
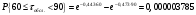
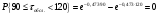
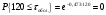
Далее, для каждого j-ого интервала определяем теоретическую частоту f_j вызовов, длительность времени обслуживания которых находится в пределах границ

---

Смотрите также файлы

• Инструкция Один человек выполняет подтягивания, другие участники ведут счет и время. Далее используя необходимые расчеты, определяют мощность.docx

• Фотосинтез и хемосинтез.doc

• Анамнез 1) Были ли вирусные инфекции (эпид паротит, вирусный гепатит, энтеровирус Коксаки В, инф мононуклеоз, краснуха, ветряная оспа, герпес, цмв, корь, грипп).docx

• Политологи я.ppt

• Педагогика оулы ббк 74. 00 П24.doc