ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 125
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Национальный минерально-сырьевой университет «Горный»
Кафедра общей и технической физики
физика
ФИЗИКА ТВЕРДОГО ТЕЛА
Методические указания к расчетно-графическим работам для студентов бакалавриата направлений подготовки 210100 и 140400
САНКТ-ПЕТЕРБУРГ
2015
УДК 531/534 (073)
ФИЗИКА. ФИЗИКА ТВЕРДОГО ТЕЛА. Методические указания расчетно-графическим работам/ Национальный минерально-сырьевой университет «Горный» / сост. Ю.И. Кузьмин, Н.С. Пщелко. СПб, 2015. —32 с.
Приведены рекомендации к выполнению расчетно-графических работ, теоретические основы дисциплины, задания для работ, пример решения задачи, библиографический список.
Предназначены для студентов направления подготовки бакалавриата 210100 «Электроника и наноэлектроника» по профилю «Промышленная Электроника» и 140400 «Электроэнергетика и электротехника» Национального минерально-сырьевого университета «Горный».
Табл. 2. Ил. 6. Библ.: 8 назв.
Научный редактор: проф. Н.С. Пщелко.
| | © Национальный минерально-сырьевой университет «Горный», 2015 г. |
РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ
РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
Вопросы и задачи, содержащиеся в пособие, охватывают существенную часть курса физики твердого тела, входящего в спецкурсы физики: «физика конденсированного состояния» и «физические основы полупроводниковой электроники» и способствуют более глубокому усвоению теоретического материала данного раздела.
Выполнение расчетно-графической работы предполагает достаточно большой объем самостоятельной работы студента.
При выполнении расчетно-графической работы (РГР) по физике твердого тела необходимо оформить отчет в печатном виде на листах формата А4 следующего содержания.
1. Титульный лист – согласно правилам университета Горный.
2. Теоретические основы работы:
2.1. Явление, изучаемое в РГР.
2.2. Определение основных физических понятий, объектов, процессов и величин, касающихся данной работы.
3. Расчетная часть:
3.1. Задание в соответствии с вариантом.
3.2. Расчет с пояснениями.
3.3. Графики.
4. Анализ результатов. Заключение.
При решении задачи необходимо:
а) сопровождать используемые при решении законы, уравнения и соотношения, пояснениями, мотивирующими решение;
б) представить результат в общем виде, т.е. преобразовать выражение для определяемой величины так, чтобы в него входили лишь буквенные обозначения величин, заданных в формулировке задания и необходимые физические константы;
в) проверить размерность величин, полученных в результате решения;
г) выполнить необходимые вычисления, представить результат в Международной системе единиц и сформулировать полный ответ в соответствии с вопросами задания.
При построении графиков, указанных в задании, следует:
— представить таблицы с данными для построения графиков;
— указать аналитическое выражение функциональной зависимости, которую необходимо построить;
— указать на осях координат физические величины и единицы их измерения.
Анализ и выводы по результатам работы должны отражать суть изучаемого физического явления.
К защите допускаются студенты, подготовившие отчёт в соответствии с требованиями по пунктам 1−4 и сдавшие его на проверку в установленные сроки. После проверки преподавателем содержания отчета, при наличии ошибок и недочетов, работа возвращается студенту на доработку. При соблюдении всех требований к оформлению отчета, правильном выполнении задания и решения соответствующей задачи студенту назначается аудиторная защита.
Для успешной защиты отчета необходимо изучить теоретический материал по данной теме, а также освоить математический аппарат, необходимый для решения задачи расчетно-графической работы. Во время защиты студент должен уметь ответить на вопросы преподавателя в полном объеме теоретического и методического содержания данной расчетно-графической работы, уметь самостоятельной вывести необходимые расчётные формулы, выполнить анализ полученных зависимостей и прокомментировать полученные результаты.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ФИЗИКИ ТВЕРДОГО ТЕЛА
ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
СОБСТВЕННЫЕ (БЕСПРИМЕСНЫЕ) ПОЛУПРОВОДНИКИ
К типичным полупроводникам относятся кремний (
) и германий (
). Эти элементы принадлежат к IV группе Периодической системы элементов. На внешней оболочке их атомов находятся четыре валентных электрона. Ширина запрещенной зоны германия равна 0,72 эВ, кремния — 1,12 эВ. Кристаллическая решетка этих полупроводников имеет одинаковую тетраэдрическую структуру. Двумерная (плоскостная) модель кристаллической решетки имеет вид, показанный на рис.1, а (на примере германия).
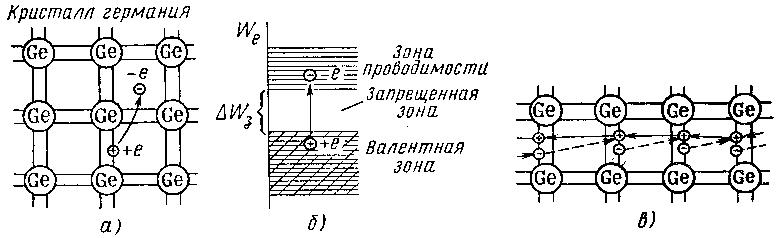
Рис. 1. Возникновение свободного электрона и дырки в кристалле полупроводника (а) и отражение этого процесса на энергетической диаграмме (б); схема движения дырки в кристалле полупроводника (в).
В отсутствие структурных дефектов и при Т = 0 К четыре валентных электрона внешней электронной оболочки каждого атома участвуют в так называемых парноэлектронных или ковалентных связях с соседними атомами. Эти связи характеризуются перекрытиями внешней электронной оболочки каждого атома с внешними электронными оболочками рядом расположенных четырех атомов кристалла. При таком перекрытии каждые два электрона принадлежат двум соседним атомам и все четыре электрона внешней оболочки атома участвуют в создании парноэлектронных связей с четырьмя соседними атомами. Парноэлектронные связи показаны на рис. 1, а в виде двух параллельных линий, связывающих атомы, расположенные в соседних узлах кристаллической решетки.
Участие всех электронов атомов кристалла в создании ковалентных связей между атомами свидетельствует о нахождении электронов на уровнях энергии валентной зоны (рис. 1, б). Повышение температуры кристалла вызывает увеличение энергии фононов. При некоторой температуре энергия фонона становится достаточной для освобождения электрона от связей с атомами кристаллической решетки. Валентный электрон освобождается от связей и становится свободным (рис. 1, а
). Освобождение электрона от связей с атомами соответствует на энергетической диаграмме (рис. 1, б). Свободный электрон способен изменять свою энергию и перемещаться между узлами кристаллической решетки под воздействием электрического поля, т.е. участвовать в создании тока.
Образование свободного электрона сопровождается разрывом ковалентной связи между атомами и появлением в месте разрыва так называемой дырки (рис. 1, а). Отсутствие электрона в ковалентной связи равносильно появлению в данном месте положительного заряда, который и приписывают дырке. На энергетической диаграмме (рис.1, б) образование дырки после перехода электрона в зону проводимости отождествляют с появлением вакантного уровня энергии в валентной зоне, позволяющего электронам валентной зоны (находящимся в ковалентных связях с атомами) изменять энергию под воздействием электрического поля, т.е. перемещаться в кристалле от атома к атому и участвовать в создании тока.
Фактическое перемещение валентных электронов под воздействием внешнего электрического поля при их последовательном заполнении образовавшегося разрыва ковалентной связи формально может быть заменено движением дырки между узлами кристаллической решетки в противоположном направлении. Действительно, валентный электрон, получив необходимую энергию, заполняет (компенсирует) дырку с приближением к ней. Дырка исчезает, и восстанавливается ковалентная связь у данного атома, но возникает новая дырка в той ковалентной связи, откуда ушел электрон. Исчезновение дырки в одном месте кристалла и ее появление в другом учитывают (условно) как движение дырки (рис.1, в).
Важность учета движения дырок как самостоятельных носителей заряда обусловливается различием в подвижностях свободных электронов и валентных электронов, перемещающихся по вакантным уровням энергии.
При температуре выше абсолютного нуля переход из валентной зоны в зону проводимости возможен у многих электронов. В результате этого процесса, получившего название термогенерации носителей заряда