где _Σ — результирующая подвижность носителей заряда в полупроводнике; _i— подвижность, обусловленнаяiмеханизмом рассеяния. Так, например, в области высоких температур _Σ контролируется вкладом в рассеяние тепловых колебаний решетки , и с ростом температуры уменьшается. В области низких температур, когда вклад решеточного рассеяния в _Σ мал, носители заряда, имеющие малую , длительное время оказываются в поле кулоновских сил (притяжения или отталкивания) ионизированных примесей. Именно этот механизм рассеяния «контролирует» _Σ в полупроводниках при низких температурах. Поэтому подвижность носителей заряда в зависимости от температуры определяются полуэмпирическим соотношением вида:

, (7)

где aи b — постоянные величины.

Качественная зависимость ln_Σ(T) в кристаллах вида (7) представлена на рис. 5. На этом рисунке кривые 1 и 2 иллюстрируют тот факт, что возрастание концентрации примесей (N_пр1<N_пр2) уменьшается _Σ в области низких температур, оставляя неизменным механизм решеточного рассеяния в кристалле.

_{Решеточное рассеяние на акустических фононах преобладает при T >100 K. При этом в области истощения примеси, когда можно положить}





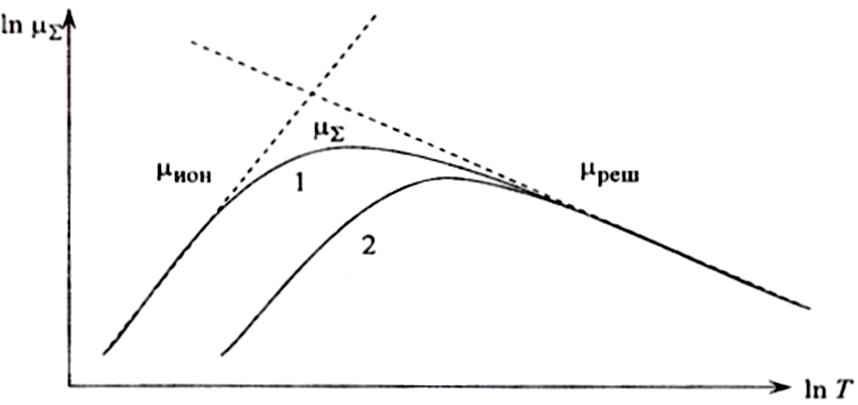
Рис. 5. Температурная зависимость подвижности носителей заряда
в полупроводниках с различными концентрациями примеси. N_пр1пр2.

удельная электропроводность может уменьшаться с увеличение температуры за счет уменьшения подвижности носителей _Σ(T) из-за рассеяния носителей заряда на акустических фононах.
ЗАДАНИЕ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ

РАБОТЫ
Тема: расчет температурной зависимости
электропроводности примесного полупроводника
Формулировка задания:

Имеется слабо легированный полупроводник на основе германия или кремния с донорной или акцепторной примесью. Электропроводность такого полупроводника определяется концентрацией основных носителей заряда и их подвижностью.

1. Определить аналитически температуру истощения примеси и температуру перехода к собственной проводимости . Определить концентрацию основных носителей заряда электронов (или дырок ) в трех температурных областях (рис. 4):

I  — область ( ) при Т = 20 К;

II — область ( ) при Т = 300 К;

III  — область ( ) при Т = 700 К.

2. Построить зависимость натурального логарифма проводимости электронного или дырочного проводника от обратной температуры в диапазоне 300 ─ 700 К.

Данные по типу полупроводника, виду и концентрации примеси, энергии ионизации выбрать по вариантам из табл. 1.
Таблица 1.

Варианты заданий

№	Полупроводник	Примесь	Тип примеси	Энергия ионизации,эВ	Концентрация примеси, 1/м3
1	Si	B	A	0,045	61021
2	Ge	B	A	0,0104	11021
3	Si	Al	A	0,057	31021
4	Ge	Al	A	0,0102	2,51021
5	Ge	P	Д	0,0120	21021
6	Si	P	Д	0,044	51021
7	Ge	As	Д	0,0127	41021
8	Si	As	Д	0,049	31021
9	Ge	Ga	A	0,0108	7,51021
10	Si	Ga	A	0,065	81021
11	Ge	In	A	0,0108	1,51021
12	Si	In	A	0,16	11021
13	Ge	Sb	Д	0,0096	6,51021
14	Si	Sb	Д	0,039	1,51021
15	Si	Bi	Д	0,3	91021
16	Si	Ni	Д	0,069	8,51021
17	Ge	Bi	Д	0,01	11021
18	Si	B	A	0,045	21021
19	Si	As	Д	0,049	11022
20	Ge	As	Д	0,0127	21022
21	Ge	Ga	A	0,0108	21021
22	Si	Ga	A	0,065	11021
23	Ge	Li	Д	0,0093	31021
24	Si	Li	Д	0,033	51021
25	Ge	Cu	Д	0,04	41021

Указания по выполнению:

1.Формулы для расчета концентрации электронов и дырок в области I имеют вид:

, (7)

, (8)

где  — энергия ионизации донорной примеси,  — энергия ионизации акцепторной примеси, и — концентрация донорной и акцепторной примеси; , — эффективные плотности состояний в зоне проводимости и в валентной зоне,  — эффективные массы электрона в зоне проводимости и дырки в валентной зоне, , — постоянная Больцмана,  — постоянная Планка.

Температура истощения примеси (рис. 4) находится из условия или (после логарифмирования) по формулам:

, . (9)

В области II истощения примеси для расчета концентрации электронов и дырок приблизительно можно принять , , поскольку процесс генерации носителей заряда за счет разрыва собственных связей в полупроводнике (область III) при этих температурах пренебрежем. Для более точного расчета к указанным значениям и надо прибавить собственную концентрацию основных носителей полупроводника.

Формулы для расчета концентрации электронов и дырок в области III имеют вид:

, (10)

где  — ширина запрещенной зоны.

Ширину запрещенной зоны принять для германия равной 0,66 эВ, а для кремния -1,08 эВ.

Температура перехода к собственной проводимости находится из условия или :

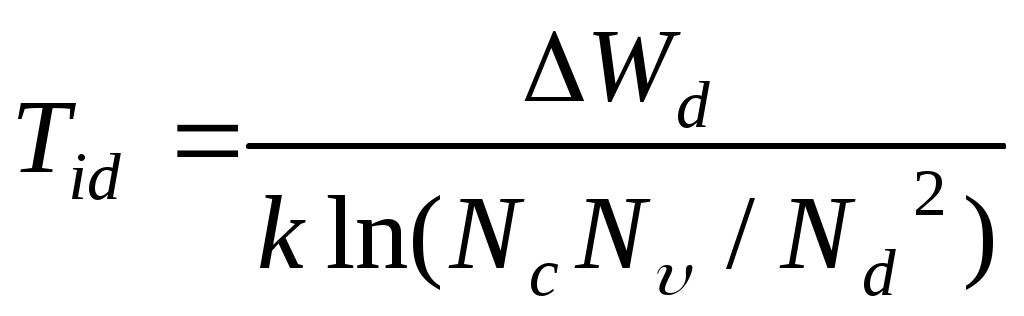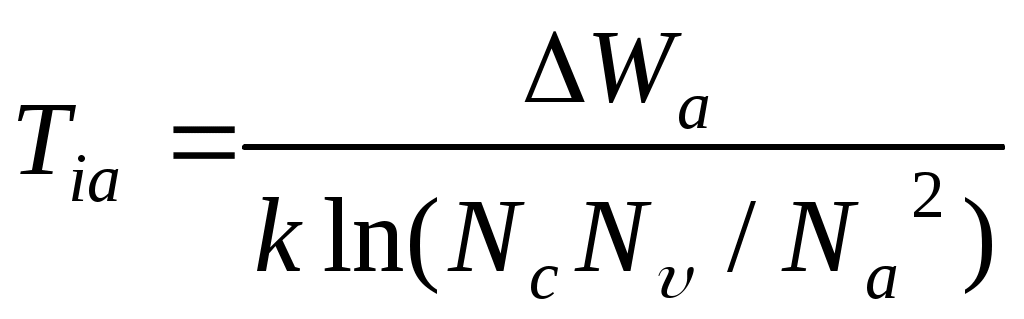, . (11)

Эффективные массы электронов и дырок для германия принять равными , а для кремния , . Здесь  — масса свободного электрона.

2. Определить электропроводность соответственно донорного полупроводника или акцепторного проводника в температурном диапазоне от 300 до 700 К по формулам:

, (12)

, (13)

где  — заряд электрона, и  — подвижности электронов и дырок. В этих формулах учитываются как носители, обусловленные наличием примесей, так и собственные носители полупроводника.

Температурную зависимость подвижности электронов и дырок, с учетом того, что в задании речь идет о температурах выше комнатной (и, следовательно, доминирующим будет механизм рассеяния на колебаниях атомов решетки), представить в виде:

, (14)

, (15)

где и  — подвижности электронов и дырок, измеренные при 300 К.

Принять для германия , , а для кремния , .

График температурной зависимости логарифма электропроводности от обратной температуры удобно строить в масштабе _.
ПРИМЕР ВЫПОЛНЕНИЯ
РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

Задание

Исследовать примесный полупроводник на основе германия (Ge) легированный мышьяком (As) с концентрацией донорной примеси =110²²1/м³ и энергией ионизации =0,0127 эВ. Определить концентрацию основных носителей (электронов) в трех областях при температурах Т = 20 К,

Т = 300 К, Т = 700 К. Определить аналитически температуру истощения примеси и температуру перехода к собственной проводимости . Определить электропроводность полупроводника на участке перехода от примесной к собственной проводимости в температурном диапазоне от 300 до 700 К. Построить график зависимости .
Решение

Приведем формулы для расчета эффективной плотности состояний в зоне проводимости и в валентной зоне к виду

= = =4,83×10²¹0,419 =2,02×10²¹ 1/м³, (16)

= = =4,83×10²¹0,225 =1,09×10²¹ 1/м³. (17)

Приведем формулу (10) для расчета концентрации донорных электронов в зоне проводимости к виду

= =(2,02×10²¹10²²) =

= 4,4910²¹ 1/м³.

Определим температуру истощения примеси из условия

.

Решая полученное трансцендентное уравнение, получим = 38 K.

Рассчитаем концентрацию электронов в зоне проводимости при Т = 20 К

n₁ = 4,49×10²¹ _{= 1,07·10}²¹ _1/м³<sub>,

то есть концентрация электронов проводимости при этой температуре на порядок меньше концентрации примесей.</sub>

Приведем формулу (10) для расчета собственных носителей заряда с учетом (16) и (17) к виду

= 1,484×10²¹ =

= 1,484×10²¹ 1/м³. (18)

Определим температуру перехода к собственной проводимости из условия

.

Решая полученное трансцендентное уравнение, получим .

Рассчитаем температурную зависимость электропроводности полупроводника по формуле (12). Для этого приведем формулу (18) к 300 К:

n_i = 1,484×10²¹ =

2,2310¹⁹ 1/м³ (19)

Рассчитаем концентрацию электронов в зоне проводимости n₂ при Т = 300 К. Для этого сложим концентрацию носителей заряда, обеспеченную всеми инизированными донорами с собственной концентрацией электронов, рассчитываемой по формуле (19)

n₂ = N_d + n_i = 1×10²² + 3,23×10¹⁹ = 1,022·10²² 1/м³,

то есть с точностью порядка двух процентов равна концентрации донорных электронов.

Рассчитаем концентрацию электронов n₃при температуре Т = 700 К по формуле (19) с учетом числа донорных электронов

n₃ = N_d + n_i = 1×10²² + 10,96×10²² = 11,96·10²² 1/м³.

Расчет показал, что при этой температуре количество собственных электронов превысило примерно на порядок количество примесных электронов.

Подставив (19), (14) и (15) в (12), получим

1,610^-192,2310¹⁹(0,39+0,18) +

+1,610^-1910²²0,39 =
= 2,03 +624 (20)

Результаты расчета по формуле (20) приведены в табл. 2.

Таблица 2

Результаты расчета

Температура полупроводника, К	300	350	400	450	500	550	600	650	700
1000/Т, К-1	3,33	2,86	2,50	2,22	2,0	1,82	1,67	1,54	1,43
Электропроводность полупроводника, (Ом·м)-1	626	507	453	480	618	912	1395	2122	3094
lnγd. (Ом·м)-1	6,44	6,23	6,12	6,17	6,43	6,82	7,24	7,66	8,06

На рис. 6. представлена искомая зависимость удельной электропроводности от обратной температуры для исследуемого полупроводника.



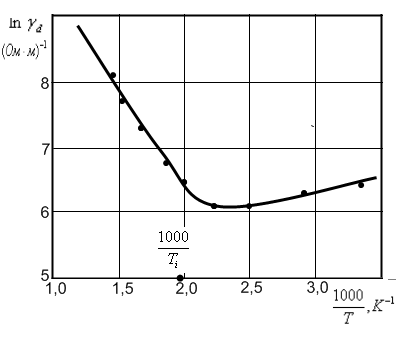
Рис.6. Зависимость удельной электропроводности от обратной температуры для исследуемого полупроводника
Как видно из данных табл. 2 и рис. 6, электропроводность полупроводника на участке истощения примесей ( ) при нагревании до температур выше комнатной, уменьшается с увеличением температуры вплоть до  — температуры перехода к собственной проводимости. В дальнейшем с увеличением температуры электропроводность резко растет (по экспоненте) за счет интенсивной генерации полупроводником собственных носителей заряда.




БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Основной:

1.  Савельев И. В. Курс физики. М.: Лань, 2008. — Т. 3.

2. Пщелко Н.С. Физические основы полупроводниковой электроники, учеб. пособие / Н. С. Пщелко, А. С. Мустафаев, К. Л. Левин — [Электронный ресурс], контрольный номер RU/IS/BASE/463508393 — СПб: Нац. минер.-сырьевой ун-т «Горный», 2013 — 254 с.

3. Чуркин Ю. В. Физика твёрдого тела / Ю. В. Чуркин, С. В. Субботин. — СПб.: Изд-во СЗТУ, 2008.

Дополнительный:

4. Трофимова Т. И. Курс физики / Т. И. Трофимова.— М.: Высшая школа, 2004 [и др. г. Изд

5. Детлаф А.А. Курс физики: учеб. пособие / А. А. Детлаф, Б. М. Яворский. — М.: Высш. шк., 2003 [и др. г. изд.].

6. Парфенова И. И.Квантовая механика, физика твёрдого тела и элементы атомной физики / И. И. Парфенова, С.В. Егоров, А.С. Мустафаев и др. — Сборник задач для студентов технических специальностей. — СПб.: СПГГИ (ТУ), 2010. — 112 с.

7. Томаев В. В., Общая физика. Физика твёрдого тела. Зонная теория твердых тел. Контактные и магнитные явления в твёрдых телах. Метод. указания к лабораторным работам / В. В. Томаев, Т. В. Стоянова, К. Л. Левин. — СПб.: 2012.

8. Шерстюк А.И. Физика твердого тела: лекции / А. И. Шерстюк. — СПб.: Изд-во СЗТУ, 2003. — 151 с.
ПРИЛОЖЕНИЯ
1. НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ

(ОКРУГЛЕННЫЕ ЗНАЧЕНИЯ)

Физическая постоянная	Обозначение	Значение
Постоянная Авогадро	NA	моль-1
Универсальная газовая постоянная	R
Постоянная Больцмана	k
Элементарный заряд	е	Кл
Скорость света в вакууме	с	м/с
Электрическая постоянная		Ф/м
Магнитная постоянная		Гн/м
Постоянная Планка		Дж
Масса электрона	m

2. МНОЖИТЕЛИ И ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ

ДЕСЯТИЧНЫХ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ
И ИХ НАИМЕНОВАНИЙ

Приставка
Наименование	Обозначение		Множитель
экса	Э		1018
пэта	П		1015
тера	Т		1012
гига	Г		109
мега	М		106
кило	к		103
гекто	г		102
Дека	да		101
Деци	д	10–1
Санти	с	10–2
Милли	м	10–3
Микро	мк	10–6
Нано	н	10–9
Пико	п	10–12
Фемто	ф	10–15
Атто	а	10–18

1   2   3   4   5

---

3. ЭЛЕКТРОФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ
НЕКОТОРЫХ ПОЛУПРОВОДНИКОВ

(температура комнатная)

Тип полупроводника	Ширина запрещенной зоны	Удельное сопротивление	Подвижность
	Еg		Электроны	Дырки
	эВ
Собственный германий	0,66	0,5	0,39	0,19
Собственный кремний	1,1		0,15	0,05
Арсенид галлия	1,43		0,85	0,042

4. ГРЕЧЕСКИЙ АЛФАВИТ

Обозначения букв	Названия букв
,	альфа
,	бета
,	гамма
Δ,	дельта
,	эпсилон
,	дзета
,	Эта
,	тхэта
,	йота
,	каппа
,	ламбда
,	мю
,	ню
,	кси
,	омикрон
,	пи
,	ро
,	сигма
T,	тау
,	ипсилон
,	фи
,	хи
,	пси
,	омега

---

СОДЕРЖАНИЕ
Рекомендации к выполнению расчетно-графических работ…......3

Теоретические основы физики твердого тела…………………......5

Задание для расчетно-графической работы………………………20

Пример выполнения расчетно-графической задачи……………..25

Библиографический список………………………………………..29

Приложения………………………………………………………...30

---

Смотрите также файлы

• История создания обезболивающих препаратов.docx

• Самостоятельная работа по теме Геометрические фигуры квадрат и прямоугольник. Нахождение периметра.docx

• Дипломный проектработа тема работы Разработка gsmконтроллера для систем управления беспроводным.pdf

• Кз мезгілі. 1 серуен картотекасы.docx

• В. К. Разуваев (И. О. Фамилия).docx