Файл: Сборник статей по итогам Международной научно практической конференции 04 мая 2018.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 1221
Скачиваний: 1
СОДЕРЖАНИЕ
ДОСТОВЕРИЗАЦИЯ ДАННЫХ В АСУТП НА ПРЕДПРИЯТИЯХ ПЕРЕРАБОТКИ НЕФТИ
Список использованной литературы
Список использованной литературы
Научный руководитель: Апасов Т.К.
МЕТОДЫ БОРЬБЫ С АСПО ПРИ ЭКСПЛУАТАЦИИ СКВАЖИН, ОБОРУДОВАННЫХ УЭЦН,
В УСЛОВИЯХ ДРУЖНОГО МЕСТОРОЖДЕНИЯ
Список использованной литературы
АНАЛИЗ ТЕХНИЧЕСКОГО ОТЧЕТА В СТРОИТЕЛЬСТВЕ
Список использованной литературы:
ФУНКЦИОНАЛЬНАЯ АРХИТЕКТУРА СИСТЕМЫ ДЛЯ ПРОФЕССИОНАЛЬНЫХ ИТ СЕРВИСОВ
Список использованной литературы:
ОПТИМИЗАЦИЯ РЕЖИМОВ ДОБЫВАЮЩИХ СКВАЖИН НА КАЛЬЧИНСКОМ МЕСТОРОЖДЕНИИ
ЗАРЕЗКА БОКОВЫХ СТВОЛОВ НА КАЛЬЧИНСКОМ МЕСТОРОЖДЕНИИ
Список использованной литературы:
Список использованной литературы
Список использованной литературы
В настоящее время к космической технике, используемой в военных и коммерческих целях, предъявляются все более высокие требования к ресурсу и надежности, при сохранении жестких требований по предельной массе и стоимости космического аппарата (КА). Кроме всех прочих, в космической технике остро стоит вопрос сохранения работоспособности электромеханических узлов, входящих в состав таких важных элементов КА, как гидронасосы системы терморегулирования, электромеханические исполнительные органы системы ориентации и стабилизации (СОС), приводы солнечных батарей и антенн. Самым критичным элементом данных электромеханических узлов КА является их опора, выполненная на основе шарикоподшипника. Шарикоподшипниковая опора в условиях космического пространства не может быть подвергнута обслуживанию или заменена, поэтому выход её из строя критичен как для узла КА, так и для всего КА.
Возможной альтернативой шарикоподшипниковой опоры может быть магнитная опора, желательно на постоянных магнитах, которая обеспечивает работы электромеханического узла без затрат энергии КА [1].
При разработке электромеханических узлов КА с магнитной опорой на постоянных магнитах остро встает вопрос построения адекватной модели данной опоры, путем моделирования электромагнитных полей. Поскольку взаимодействие магнитных полей в
зазоре между ротором и статором является труднопрогнозируемым, то рациональным будет применение специализированных программы для анализа процессов (САПР), происходящих в нем, что привело к необходимости численного моделирования процессов. Среди современных САПР существует ряд программ для моделирования электромагнитных полей:
-
пакет программ Femm. Достоинством является невысокая требовательность к мощности ЭВМ, доступность. Основной недостаток – это отсутствие возможности решения задач в трехмерной постановке [2]. -
пакет программ ELCUT. Достоинствами являются: отсутствие необходимости в построении густой сетки разбиения, при сохранении правильного вычисления значений на ребрах модели. При наличии в исходной модели симметрии существенно ускоряется решение задач. Кроме того, в данном пакете применен специальный вид граничных условий. Однако интерфейс остается неудобным [3]. -
пакет программ ANSYS Maxwell. Достоинствами пакета программ ANSYS Maxwell являются: наличие расширенной библиотеки свойств материалов, полная автоматизация разбиения модели на конечные элементы и расчетов при различных сочетаниях параметров, поддержка и редактирование скриптов в особых ситуациях. Также существуют дополнительные программы, расширяющие возможности Maxwell (ePhysics, Simplorer), а также программы, упрощающие процесс моделирования в Maxwell (RMxprt, PExprt, Optimetrics, Maxwell Circuit Editor, Q3D Extractor) [4]. -
пакет программ Ansys Multiphysics. Достоинством пакета программ Ansys Multiphysics является способность решать любые электромагнитные и тепловые задачи в 2D и 3D, с возможностью наложения механической составляющей. Недостатком является довольное большое время расчета, несовершенный построитель сетки, необходимость в серьезных компьютерных ресурсах [5].
Перечисленные ранее пакеты программ используют для расчетов метод конечных элементов, основанный на аппроксимации непрерывной функции (температуры, напряжённости магнитного поля, магнитной индукции, перемещения и т.д.) дискретной моделью, которая строится на множестве кусочно - непрерывных функций [6].
На фоне рассматриваемых аналогов наилучшей с точки зрения простоты освоения и широты возможностей для проведения электромагнитных расчетов наиболее подходит пакет программ ANSYS Maxwell [7].
Для решения задач магнитостатики ANSYS Maxwell использует в своем решателе основные уравнения (1.1 и 1.2)
Ax⃗H→ = ????→ , (1.1)
A · ⃗B→ = 0, (1.2)
кроме того, используется следующая важная зависимость (1.3):
????⃗→ = ????0(????⃗→ + ????⃗→) = ????0????????????⃗→ + ????0????⃗→???? , (1.3)
где:
????⃗→ – напряженность магнитного поля;
????⃗→ – плотность магнитного потока;
– плотность тока проводимости;
⃗ ⃗⃗⃗⃗
– постоянное намагничивание;
– магнитная проницаемость вакуума;
– относительная магнитная проницаемость.
Для создания в среде ANSYS Maxwell математической модели опоры построена геометрическая пространственная модель (рис. 1), состоящая из двух основных частей: ротора 1 и статора 2. Конические элементы ротора и статора выполнены из неодим - железа NdFe с коэрцитивной силой 837999,999 А / м с осевой намагниченностью однонаправленной относительно друг друга. Цилиндрические элементы модели выполнены из магнитомягкого металла с удельной электрической проводимостью 1610000 См / м и являются магнитопроводом.
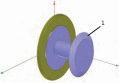
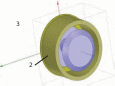
Рис. 1 Геометрическая пространственная модель
Задана поверхностная сетка (рис. 2) разбиения всех составных частей модели на конечные элементы. Определены граничные условия моделируемой области 3 (рис. 1), таким образом, чтобы исключить ошибку влияния границ на результаты расчетов, рассматривая ее в бесконечно пустом пространстве, и одновременно не завышая время анализа программы. Такая методика часто применяется при небольших объектах или частях сложных систем [6].
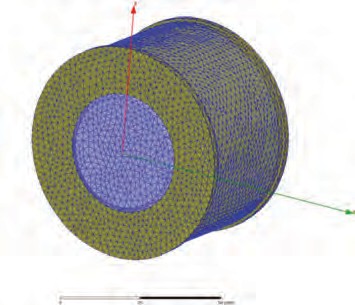
Рис. 2 Геометрическая пространственная модель
с поверхностной сеткой разбиения на конечные
элементы
По результатам просчета модели программой отображается распределение магнитного поля, направление вектора и величину напряженности магнитного поля (рис. 3). Как видно, рабочий магнитный поток, создающий взаимные силы отталкивания, сосредоточен на участках 1 и 2. Распределение магнитного потока на участке 2, представляет основной интерес, поскольку важно для функционирования опоры.
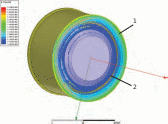
Рис. 3 Распределение магнитного поля в зазоре опоры
Модель позволяет рассчитать трехмерное пространственное распределение электрического магнитного поля, определить магнитную индукцию, напряженность магнитного поля в каждой точке зазора и на основании этого сделать вывод о величине и направлении силы магнитного взаимодействия ротора и статора магнитной опоры ЭМИО. Данная модель может быть применена для проектирования реальной магнитной опоры используемой в электромеханических устройствах космического аппарата, таких как двигатели - маховики или гиростабилизаторы системы ориентации.