ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 704
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Et , оцените относительную ширину / излучаемой спектральной линии, если не происходит ее уширения за счет других процессов.
Задача 624. Электрон движется в атоме водорода по третьей стационарной боровской орбите. Используя соотношение неопределенностей px , оцените неточность x в определении координаты электрона, если известно, что допускаемая неточность в определении его скорости движения составляет v 10 % от ее величины.
Задача 625. Приняв, что в атомном ядре минимальная энергия нуклона Еmin 10 МэВ, оцените, исходя из соотношения неопределенностей px , минимальные линейные размеры lmin ядра.
Задача 626. Среднее время жизни атома в возбужденном состоянии t 10 нс.
При переходе атома в нормальное состояние испускается фотон с длиной волны 600 нм. Оцените отношение естественной ширины E энергетического уровня, на который был возбужден электрон, к энергии Е, излученной атомом.
Задача 627. Неопределенность x координаты движущейся микрочастицы равна
дебройлевской длине волны . Используя соотношение неопределенностей px , оцените относительную неопределенность p/р импульса этой микрочастицы.
Задача 628. Координаты электрона и пылинки массой m2 1 нг установлены с одинаковой точностью. Вычислите отношение v1/v2 неопределенностей скоростей движения электрона и пылинки.
Задача 629. В возбужденном состоянии среднее время жизни атома t 10 нс. При переходе атома в нормальное состояние испускается фотон с длиной волны 400 нм.
Используя соотношение неопределенностей Et , оцените естественную ширину
излучаемой спектральной линии, если не происходит ее уширения за счет других процессов.
Задача 630. Моноэнергетический пучок электронов, прошедших в однородном электрическом поле ускоряющую разность потенциалов U 20 кВ, в центре экрана электроннолучевой трубки, длина которой l 0,5 м, высвечивает пятно радиусом r 103 см. Пользуясь соотношением неопределенностей px , оцените, во сколько раз радиус r пятна больше неопределенности координаты x электрона на экране в направлении, перпендикулярном оси трубки.
Задача 631. Частица находится в бесконечно глубоком
, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l в возбужденном состоянии, определяемом главным квантовым числом n 2. Определите, в каких точках интервала
0 x l плотность вероятности 2(x)2 нахождения частицы максимальна и минимальна. Решение поясните графически.
Задача 632. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l в возбужденном состоянии, определяемом главным квантовым числом n 2. Во сколько раз вероятность W1 местонахождения электрона в средней трети (1/3l x 2/3l) больше вероятности W2 местонахождения электрона в средней четверти (3/8l x 5/8l) ящика?
Задача 633. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l 0,2 нм. Определите (в электрон-вольтах) минимальную разность Emin энергетических уровней электрона.
Задача 634. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками в возбужденном состоянии, определяемом главным квантовым числом n 4. Какова вероятность W обнаружения частицы в крайней четверти (0 x 1/4l) ящика?
Задача 635. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками. Найдите отношение разности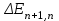
соседних энергетических уровней к энергии En частицы в следующих трех случаях: 1) n 3; 2) n 10; 3) n . Поясните полученные результаты.
Задача 636. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l. Определите, в каких точках интервала 0 x l плотности вероятности нахождения электрона на первом 1(x)2 и втором 2(x)2 энергетических уровнях одинаковы? Вычислите плотность вероятности для этих точек. Решение поясните графически.
Задача 637. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l. Вычислите отношение вероятностей W1/W2 обнаружения частицы на первом n1 1 и втором
n2 2 энергетических уровнях в средней трети (1/3l x 2/3l) ящика.
Задача 638. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с абсолютно непроницаемыми стенками шириной l 0,2 нм. Энергия электрона в ящике Е 37,8 эВ. Определите порядковый номер n энергетического уровня электрона и отвечающее электрону модуль волнового вектора k.
Задача 639. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l с непроницаемыми стенками в основном состоянии. Какова вероятность W обнаружения частицы в крайней трети (0 x 1/3l) ящика?
Задача 640. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l 6 нм в возбужденном состоянии, определяемом главным квантовым числом n 2. Определите температуру Т, при которой дискретность энергетического спектра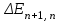
электрона сравнима с его средней кинетической энергией Ek теплового движения.
Задача 641. За время t 1 сут активность радиоактивного изотопа уменьшилась от А1 118 ГБк до А2 7,4 ГБк. Определите период полураспада Т1/2 этого нуклида.
Задача 642. Какая часть k начального количества атомных ядер распадется за время
t 1 год в радиоактивном изотопе тория 229Th?
Задача 643. Определите активность А радиоактивного изотопа фосфора 32Р массой
m 1 мг.
Задача 644. За время t 8 сут распалось часть k 3/4 начального количества атомных ядер радиоактивного изотопа. Определите период полураспада T1/2 этого нуклида.
Задача 645. Счетчик -частиц, установленный вблизи радиоактивного изотопа,
при первом измерении зарегистрировал за единицу времени число N1 1400 мин1 частиц, а при втором измерении через время t 4 ч зарегистрировал за единицу времени число N2 400 мин1 частиц. Определите период полураспада Т1/2 этого изотопа.
Задача 646. Определите, на сколько процентов уменьшится активность радиоактивного изотопа иридия 192Ir за время t 30 сут.
Задача 647. Какая часть k начального количества атомных ядер радиоактивного нуклида распадется за время
t, равное средней продолжительности жизни радиоактивного ядра этого нуклида?
Задача 648. Масса радиоактивного изотопа стронция 90Sr m1 1 мг. Какова масса m2 радиоактивного изотопа урана 238U, имеющего такую же активность?
Задача 649. Вычислите удельную (массовую) активность а радиоактивного изотопа
кобальта 60Со.
Задача 650. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, регистрирует поток -частиц. При первом измерении счетчик частиц зарегистрировал поток Ф1 87 с1, а по истечении времени t 1 сут счетчик зарегистрировал поток Ф2 22 с1. Определите период полураспада Т1/2 изотопа серебра.
Задача 651. Определите минимальную энергию Еmin, которую нужно затратить, чтобы оторвать один нейтрон от атомного ядра азота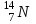
.
Задача 652. При ядерной реакции 9Be(, n)12C освобождается энергия Q 5,69 МэВ. Пренебрегая кинетическими энергиями ядер бериллия и гелия и принимая их суммарный импульс равным нулю, определите кинетические энергии Т1и Т2 и импульсы р1 и p2 продуктов реакции.
Задача 653. Определите удельную энергию Еуд связи атомных ядер алюминия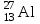
и свинца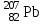
.
Задача 654. Вычислите энергию Q и определите тип следующих ядерных реакций,
записанных в сокращенном виде: а) 7Li(, n)10В и б) 19F(p, )16O.
Задача 655. Определите минимальную энергию Еmin, которую нужно затратить, чтобы разделить атомное ядро гелия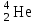
на две одинаковые части.
Задача 656. Атомное ядро углерода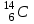
выбросило отрицательно заряженную
-частицу и антинейтрино. Определите полную энергию Q -распада ядра.
Задача 657. Атомное ядро, поглотившее -фотон с длиной волны 0,2 пм, пришло
в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные
стороны. Определите энергию связи
Есв атомного ядра, если суммарная кинетическая энергия нуклонов Т 0,6 МэВ.
Задача 658. Сокращенная запись ядерной реакции имеет вид: 9Be(n, )10Be. Вычислите энергию Q и определите тип этой ядерной реакции, если энергия связи атомного ядра изотопа бериллия 9Ве Есв1 58,16 МэВ, а энергия связи атомного ядра изотопа бериллия 10Ве Есв2 64,98 МэВ.
Задача 659. Удельные энергии связи атомных ядер неона 20Ne, углерода 12C и гелия 4Hе равны соответственно Еуд1 8,03 МэВ/нуклон, Еуд2 7,68 МэВ/нуклон и Еуд3
7,07 МэВ/нуклон. Определите минимальную энергию Еmin, необходимую для разделения атомного ядра неона 20Ne на атомное ядро углерода 12С и две -частицы.
Задача 660. Тепловая мощность атомной электростанции Р 10 МВт. Принимая,
что при распаде одного атомного ядра изотопа урана 235U выделяется энергия Q 200 МэВ, определите массовый суточный расход mt ядерного горючего в ядерном реакторе атомной электростанции, если ее КПД 20 %.
Задача 661. Найдите отношение кв/T средней энергии трехмерного квантового
осциллятора к средней энергии теплового движения молекул идеального газа при температуре Т E, где E – характеристическая температура Эйнштейна.
Задача 662. Пользуясь квантовой теорией теплоемкости Дебая, вычислите удельную теплоемкость с алюминия при температуре Т D, где D – характеристическая температура Дебая.
Задача 663. Характеристическая температура Эйнштейна для меди E 254 К. Используя квантовую теорию теплоемкости Эйнштейна, определите коэффициент квазиупругой связи атомов в кристалле меди.
Задача 664. При температуре Т 20 К молярная теплоемкость железа Cm
0,153 Дж/(моль·К). Считая условие Т D выполненным, вычислите характеристическую температуру D Дебая для железа.
Задача 665. Система, состоящая из числа N 1025 трехмерных квантовых независимых осцилляторов, находится при температуре Т E 300 К, где E – характеристическая температура Эйнштейна. Определите энергию U этой системы квантовых осцилляторов.
Задача 666. Цинк находится при температуре T 10 К. Считая условие Т D выполненным, по квантовой теории теплоемкости Дебая вычислите теплоемкость
Задача 624. Электрон движется в атоме водорода по третьей стационарной боровской орбите. Используя соотношение неопределенностей px , оцените неточность x в определении координаты электрона, если известно, что допускаемая неточность в определении его скорости движения составляет v 10 % от ее величины.
Задача 625. Приняв, что в атомном ядре минимальная энергия нуклона Еmin 10 МэВ, оцените, исходя из соотношения неопределенностей px , минимальные линейные размеры lmin ядра.
Задача 626. Среднее время жизни атома в возбужденном состоянии t 10 нс.
При переходе атома в нормальное состояние испускается фотон с длиной волны 600 нм. Оцените отношение естественной ширины E энергетического уровня, на который был возбужден электрон, к энергии Е, излученной атомом.
Задача 627. Неопределенность x координаты движущейся микрочастицы равна
дебройлевской длине волны . Используя соотношение неопределенностей px , оцените относительную неопределенность p/р импульса этой микрочастицы.
Задача 628. Координаты электрона и пылинки массой m2 1 нг установлены с одинаковой точностью. Вычислите отношение v1/v2 неопределенностей скоростей движения электрона и пылинки.
Задача 629. В возбужденном состоянии среднее время жизни атома t 10 нс. При переходе атома в нормальное состояние испускается фотон с длиной волны 400 нм.
Используя соотношение неопределенностей Et , оцените естественную ширину
излучаемой спектральной линии, если не происходит ее уширения за счет других процессов.
Задача 630. Моноэнергетический пучок электронов, прошедших в однородном электрическом поле ускоряющую разность потенциалов U 20 кВ, в центре экрана электроннолучевой трубки, длина которой l 0,5 м, высвечивает пятно радиусом r 103 см. Пользуясь соотношением неопределенностей px , оцените, во сколько раз радиус r пятна больше неопределенности координаты x электрона на экране в направлении, перпендикулярном оси трубки.
Задача 631. Частица находится в бесконечно глубоком
, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l в возбужденном состоянии, определяемом главным квантовым числом n 2. Определите, в каких точках интервала
0 x l плотность вероятности 2(x)2 нахождения частицы максимальна и минимальна. Решение поясните графически.
Задача 632. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l в возбужденном состоянии, определяемом главным квантовым числом n 2. Во сколько раз вероятность W1 местонахождения электрона в средней трети (1/3l x 2/3l) больше вероятности W2 местонахождения электрона в средней четверти (3/8l x 5/8l) ящика?
Задача 633. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l 0,2 нм. Определите (в электрон-вольтах) минимальную разность Emin энергетических уровней электрона.
Задача 634. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками в возбужденном состоянии, определяемом главным квантовым числом n 4. Какова вероятность W обнаружения частицы в крайней четверти (0 x 1/4l) ящика?
Задача 635. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками. Найдите отношение разности
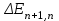соседних энергетических уровней к энергии En частицы в следующих трех случаях: 1) n 3; 2) n 10; 3) n . Поясните полученные результаты.Задача 636. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l. Определите, в каких точках интервала 0 x l плотности вероятности нахождения электрона на первом 1(x)2 и втором 2(x)2 энергетических уровнях одинаковы? Вычислите плотность вероятности для этих точек. Решение поясните графически.
Задача 637. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l. Вычислите отношение вероятностей W1/W2 обнаружения частицы на первом n1 1 и втором
n2 2 энергетических уровнях в средней трети (1/3l x 2/3l) ящика.
Задача 638. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с абсолютно непроницаемыми стенками шириной l 0,2 нм. Энергия электрона в ящике Е 37,8 эВ. Определите порядковый номер n энергетического уровня электрона и отвечающее электрону модуль волнового вектора k.
Задача 639. Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l с непроницаемыми стенками в основном состоянии. Какова вероятность W обнаружения частицы в крайней трети (0 x 1/3l) ящика?
Задача 640. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике с непроницаемыми стенками шириной l 6 нм в возбужденном состоянии, определяемом главным квантовым числом n 2. Определите температуру Т, при которой дискретность энергетического спектра
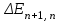электрона сравнима с его средней кинетической энергией Ek теплового движения.Задача 641. За время t 1 сут активность радиоактивного изотопа уменьшилась от А1 118 ГБк до А2 7,4 ГБк. Определите период полураспада Т1/2 этого нуклида.
Задача 642. Какая часть k начального количества атомных ядер распадется за время
t 1 год в радиоактивном изотопе тория 229Th?
Задача 643. Определите активность А радиоактивного изотопа фосфора 32Р массой
m 1 мг.
Задача 644. За время t 8 сут распалось часть k 3/4 начального количества атомных ядер радиоактивного изотопа. Определите период полураспада T1/2 этого нуклида.
Задача 645. Счетчик -частиц, установленный вблизи радиоактивного изотопа,
при первом измерении зарегистрировал за единицу времени число N1 1400 мин1 частиц, а при втором измерении через время t 4 ч зарегистрировал за единицу времени число N2 400 мин1 частиц. Определите период полураспада Т1/2 этого изотопа.
Задача 646. Определите, на сколько процентов уменьшится активность радиоактивного изотопа иридия 192Ir за время t 30 сут.
Задача 647. Какая часть k начального количества атомных ядер радиоактивного нуклида распадется за время
t, равное средней продолжительности жизни радиоактивного ядра этого нуклида?
Задача 648. Масса радиоактивного изотопа стронция 90Sr m1 1 мг. Какова масса m2 радиоактивного изотопа урана 238U, имеющего такую же активность?
Задача 649. Вычислите удельную (массовую) активность а радиоактивного изотопа
кобальта 60Со.
Задача 650. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, регистрирует поток -частиц. При первом измерении счетчик частиц зарегистрировал поток Ф1 87 с1, а по истечении времени t 1 сут счетчик зарегистрировал поток Ф2 22 с1. Определите период полураспада Т1/2 изотопа серебра.
Задача 651. Определите минимальную энергию Еmin, которую нужно затратить, чтобы оторвать один нейтрон от атомного ядра азота
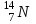.Задача 652. При ядерной реакции 9Be(, n)12C освобождается энергия Q 5,69 МэВ. Пренебрегая кинетическими энергиями ядер бериллия и гелия и принимая их суммарный импульс равным нулю, определите кинетические энергии Т1и Т2 и импульсы р1 и p2 продуктов реакции.
Задача 653. Определите удельную энергию Еуд связи атомных ядер алюминия
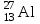
и свинца
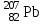.Задача 654. Вычислите энергию Q и определите тип следующих ядерных реакций,
записанных в сокращенном виде: а) 7Li(, n)10В и б) 19F(p, )16O.
Задача 655. Определите минимальную энергию Еmin, которую нужно затратить, чтобы разделить атомное ядро гелия
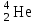на две одинаковые части.Задача 656. Атомное ядро углерода
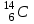выбросило отрицательно заряженную -частицу и антинейтрино. Определите полную энергию Q -распада ядра.
Задача 657. Атомное ядро, поглотившее -фотон с длиной волны 0,2 пм, пришло
в возбужденное состояние и распалось на отдельные нуклоны, разлетевшиеся в разные
стороны. Определите энергию связи
Есв атомного ядра, если суммарная кинетическая энергия нуклонов Т 0,6 МэВ.
Задача 658. Сокращенная запись ядерной реакции имеет вид: 9Be(n, )10Be. Вычислите энергию Q и определите тип этой ядерной реакции, если энергия связи атомного ядра изотопа бериллия 9Ве Есв1 58,16 МэВ, а энергия связи атомного ядра изотопа бериллия 10Ве Есв2 64,98 МэВ.
Задача 659. Удельные энергии связи атомных ядер неона 20Ne, углерода 12C и гелия 4Hе равны соответственно Еуд1 8,03 МэВ/нуклон, Еуд2 7,68 МэВ/нуклон и Еуд3
7,07 МэВ/нуклон. Определите минимальную энергию Еmin, необходимую для разделения атомного ядра неона 20Ne на атомное ядро углерода 12С и две -частицы.
Задача 660. Тепловая мощность атомной электростанции Р 10 МВт. Принимая,
что при распаде одного атомного ядра изотопа урана 235U выделяется энергия Q 200 МэВ, определите массовый суточный расход mt ядерного горючего в ядерном реакторе атомной электростанции, если ее КПД 20 %.
Задача 661. Найдите отношение кв/T средней энергии трехмерного квантового
осциллятора к средней энергии теплового движения молекул идеального газа при температуре Т E, где E – характеристическая температура Эйнштейна.
Задача 662. Пользуясь квантовой теорией теплоемкости Дебая, вычислите удельную теплоемкость с алюминия при температуре Т D, где D – характеристическая температура Дебая.
Задача 663. Характеристическая температура Эйнштейна для меди E 254 К. Используя квантовую теорию теплоемкости Эйнштейна, определите коэффициент квазиупругой связи атомов в кристалле меди.
Задача 664. При температуре Т 20 К молярная теплоемкость железа Cm
0,153 Дж/(моль·К). Считая условие Т D выполненным, вычислите характеристическую температуру D Дебая для железа.
Задача 665. Система, состоящая из числа N 1025 трехмерных квантовых независимых осцилляторов, находится при температуре Т E 300 К, где E – характеристическая температура Эйнштейна. Определите энергию U этой системы квантовых осцилляторов.
Задача 666. Цинк находится при температуре T 10 К. Считая условие Т D выполненным, по квантовой теории теплоемкости Дебая вычислите теплоемкость