Задача 115. Боёк (ударная часть) свайного молота массой т₁  500 кг падает с некоторой высоты на сваю массой т₂  120 кг. Принимая полезной энергию, затраченную на вбивание сваи в грунт, пренебрегая изменением потенциальной энергии сваи при ее углублении и считая удар неупругим, определите КПД  удара бойка о сваю.

Задача 116. Частица массой т₁  10^25 кг обладает импульсом р₁  510^20 кгм/с. Определите импульс 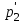, который передаст эта частица при лобовом (прямом, центральном) ударе, сталкиваясь абсолютно упруго с другой частицей массой т₂  410^25 кг, которая до соударения покоилась.

Задача 117. Два абсолютно неупругих шара массами т₁  2 кг и т₂  3 кг движутся
соответственно со скоростями v₁  8 м/с и v₂  4 м/с. Определите увеличение U внутренней энергии шаров при их прямом, центральном ударе в случае, когда меньший шар нагоняет больший.

Задача 118. Из артиллерийского орудия производилась стрельба в горизонтальном
направлении. Когда орудие было закреплено неподвижно, снаряд вылетел со скоростью
v₁  600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью v₂  580 м/с. Определите скорость v, с которой при этом откатилось орудие.

Задача 119. Два шара массами т₁  10 кг и т₂  15 кг подвешены на одинаковых тонких невесомых нерастяжимых нитях длиной l  2 м так, что шары соприкасаются между собой. Меньший шар отклонили от положения равновесия на угол   60 и отпустили. Считая удар шаров прямым, центральным и неупругим, определите высоту h, на которую поднимутся оба шара после удара.

Задача 120. В деревянный шар массой т₁  8 кг, подвешенный на тонкой невесомой
нерастяжимой нити длиной l  1,8 м, попадает горизонтально летящая пуля массой т₂  4 г. Пренебрегая размером шара и считая удар пули прямым, центральным, определите скорость v₂, с которой летела пуля, если известно, что нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол   3.

Задача 121. Масса Земли в n  81,6 раза больше массы Луны. Расстояние между центрами масс Земли и Луны l  60,3R, где R – радиус Земли. На каком расстоянии r (в радиусах Земли) от Земли на прямой, проходящей через центры Земли и Луны, находится точка, в которой суммарная напряженность

---

g гравитационного поля Земли и Луны равна нулю?

Задача 122. Определите работу А, которую нужно совершить, чтобы поднять с поверхности Земли материалы для постройки цилиндрической дымоходной трубы внутренним диаметром d  2 м, наружным диаметром D  3 м и высотой h  40 м, если плотность материала трубы   2,810³ кг/м³?

Задача 123. Ускорение свободного падения на поверхности Земли в k  6,09 раза больше ускорения свободного падения на поверхности Луны, а радиус Земли в n  3,66 раза больше радиуса Луны. Определите, во сколько раз плотность _З земного вещества больше плотности _Л лунного.

---

Задача 124. Пружина с коэффициентом жесткости k  1 кН/м была сжата на величину x₁  4 см. Какую работу А нужно совершить, чтобы сжатие пружины увеличить до величины x₂  18 см?

Задача 125. Начальная скорость v_ движения ракеты, запущенной с поверхности Земли вертикально вверх, равна первой космической скорости v₁. Определите высоту h, на которую поднимется эта ракета над ее поверхностью.

Задача 126. Стальной стержень длиной l  2 м и площадью поперечного сечения
S  2 см² растягивается некоторой силой; при этом его удлинение x  0,4 см. Вычислите
потенциальную энергию П растянутого стержня и объемную плотность w потенциальной энергии.

Задача 127. Тело массой m  1 кг падает на поверхность Земли. Считая известными
радиус R Земли и ускорение g свободного падения на ее поверхности, определите работу А, которую совершат силы гравитационного поля Земли, если это тело упадет на поверхность Земли: 1) с высоты h, равной радиусу R Земли; 2) из бесконечности.

Задача 128. Гиря, положенная на верхний конец спиральной пружины, поставленной на подставке, сжимает ее на величину x  2 мм. Каково будет сжатие l пружины, если та же гиря упадет на конец пружины с высоты h  5 см?

Задача 129. Спутник обращается вокруг Земли по круговой орбите на высоте h 
 520 км. Считая известными радиус R Земли и ускорение g свободного падения на ее
поверхности, определите период Т обращения спутника.

Задача 130. Стальной стержень длиной l  1 м имеет площадь поперечного сечения S  1 см². Какую работу А нужно совершить, чтобы растянуть стержень на x  1 мм?

Задача 131. В центре скамьи Жуковского стоит человек и держит в руках за середину тонкий стержень длиной l  2,4 м и массой т  8 кг, расположенный вертикально вдоль оси вращения скамьи. Суммарный момент инерции скамьи и человека J  6 кгм². Скамья с человеком вращается по инерции без трения с частотой п₁  1 с^1. С какой частотой n₂ будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение?

Задача 132. По горизонтальной плоской поверхности без скольжения катится круглый сплошной однородный диск со скоростью v  8 м/с. Определите коэффициент сопротивления f, если диск, будучи предоставленным самому себе, остановился, пройдя путь s

---

 18 м.

Задача 133. Человек массой т₁  80 кг стоит на краю горизонтальной платформы
массой m₂  240 кг, имеющей форму диска радиусом R  2 м. Платформа может вращаться вокруг неподвижной вертикальной оси, проходящей через ее центр. Пренебрегая трением
и рассчитывая момент инерции человека как для материальной точки, найдите угловую скорость , с которой начнет вращаться платформа, если человек будет двигаться относительно платформы вдоль ее края со скоростью v  2 м/с.

Задача 134. Через неподвижный блок массой т  0,2 кг перекинута тонкая невесомая нерастяжимая гибкая нить, к концам которой прикреплены грузы массами т₁  0,3 кг и т₂  0,5 кг. Пренебрегая трением в подшипниках оси блока и проскальзыванием нити по блоку, определите ускорение a, с которым движутся грузы, и силы натяжения T₁ и Т₂ нити по обе стороны от блока во время движения грузов, если масса блока равномерно распределена по ободу.

Задача 135. На краю платформы в виде круглого однородного диска радиусом R  1 м стоит человек массой т  80 кг. Момент инерции платформы J  120 кгм². Платформа
с человеком вращается по инерции без трения вокруг неподвижной вертикальной оси
с частотой п₁  6 мин^1. Рассчитывая момент инерции человека как для материальной точки, определите частоту п₂, с которой будет вращаться платформа, если человек перейдет в ее центр.

Задача 136. Шарик массой m  100 г, привязанный к концу тонкой невесомой нерастяжимой нити длиной l₁  1 м, вращается, опираясь на горизонтальную плоскость, с частотой n₁  1 с^1. Нить укорачивается, и шарик приближается к оси вращения до расстояния l₂  0,5 м. Пренебрегая трением шарика о плоскость, найдите частоту n₂, с которой будет при этом вращаться шарик. Какую работу А совершит внешняя сила, укорачивая нить?

Задача 137. В центре скамьи Жуковского стоит человек и держит в руках прямой стержень, расположенный вертикально вдоль оси вращения скамьи. Стержень служит осью вращения колеса, радиус которого R  20 см и масса m  3 кг, расположенного на верхнем конце стержня. Скамья неподвижна, а колесо вращается с частотой n₁  10 с^1. Суммарный момент инерции человека и скамьи J  6 кгм². Пренебрегая трением и считая массу колеса равномерно распределенной по ободу, определите частоту n₂

---

вращения скамьи, если человек повернет стержень на угол   180.

Задача 138. Тонкий прямой однородный стержень длиной l  1 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В нижний конец стержня абсолютно неупруго ударяет пуля массой m  7 г, летящая со скоростью v  360 м/с перпендикулярно стержню и его оси. Определите массу М стержня, если в результате попадания пули он отклонился от вертикали на угол   60.

Задача 139. Человек, стоящий на неподвижной скамье Жуковского, ловит рукой мяч массой m  0,4 кг, летящий в горизонтальном направлении со скоростью v  20 м/с, траектория которого находится на расстоянии r  0,8 м от вертикальной оси вращения скамьи. Пренебрегая трением и рассчитывая момент инерции мяча как для материальной точки, определите угловую скорость , с которой начнет вращаться скамья с человеком, поймавшим мяч, если суммарный момент инерции человека и скамьи J  6 кгм².

Задача 140. Маховик, момент инерции которого J  50 кгм², вращается согласно уравнению   А  Bt  Ct², где А  2 рад, В  16 рад/с, С  –2 рад/с². Напишите уравнения M(t) и N(t), по которым меняются соответственно вращающий момент М и мощность N. Какова мощность N в момент времени t  3 с?

Задача 141. Углекислый газ, плотность которого   7,5 кг/м³, течет по круглой гладкой длинной трубе с внутренним диаметром d  2 см. Найдите скорость v его течения
по трубе, если известно, что за время t  30 мин через поперечное сечение трубы протекает газ массой m  0,51 кг.

Задача 142. Дождевая капля диаметром d  0,3 мм падает в воздухе. Определите
максимальную скорость v_max, которую может достичь эта капля, если коэффициент динамической вязкости воздуха   12 мкПас.

Задача 143. Смесь свинцовых дробинок с диаметрами d₁  3 мм и d₂  1 мм опустили одновременно в большой широкий сосуд с глицерином высотой h  1 м. Определите промежуток времени t, через которое раньше на дно сосуда упадут дробинки большего диаметра по сравнению с дробинками меньшего диаметра.

Задача 144. При движении шарика радиусом r₁  2,4 мм в большом широком сосуде, наполненном касторовым маслом, ламинарное обтекание наблюдается при скорости движения шарика, не превышающей v₁  10 см/с. При какой минимальной скорости v₂ движения шарика радиусом r₂

---

Смотрите также файлы

• История доктринального исследования уголовной политики в России и за рубежом. Понятие и значение уголовной политики. Впервые понятие уголовная политика.docx

• Расчет цвд влажнопаровой турбины аэс.docx

• Водоросли.docx

• Поход в зоопарк Информацию 2 слайда оформить в виде схемы. Информацию 4 слайда оформить в виде таблицы.pptx

• Решение. 0,9 1 0,9 0,1 5 2.docx