ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 216
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Свойства логарифмов | Свойства логарифмов | Свойства логарифмов | Свойства логарифмов |
| Вариант – 5 | Вариант – 6 | Вариант – 7 | Вариант – 8 |
а) 4; б) 9; в) 2; г) -2
а) 2; б) -1; в)
а) 5; б)32; в) lg32; г) 6
а) 6; б) 2; в) -2; г) -6
а)24; б) 4; в) 2; г) – 24
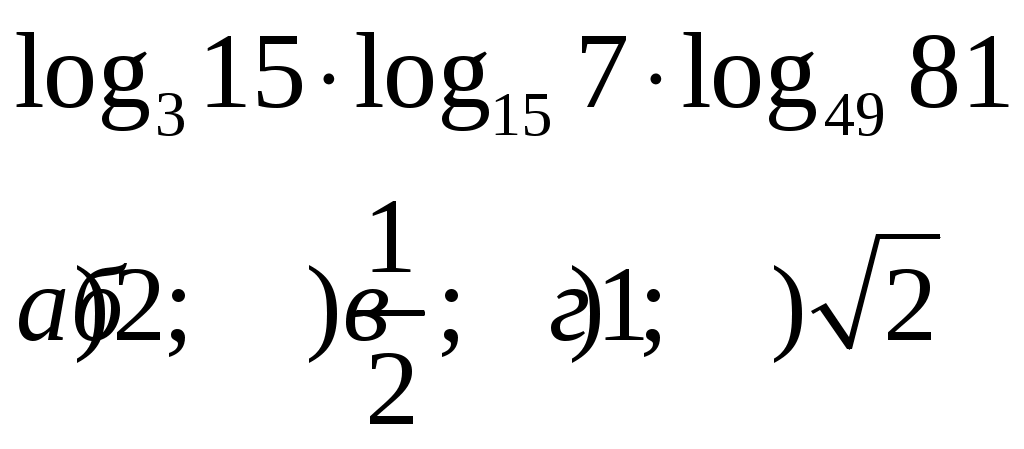
а) 2a+ 2b;б) 3a+ 2b; в) a - b; г) a + b
а) 2; б) 0,5; в) 1; г) -1 |
а) 125; б) 3; в) -3; г) 4
а) 1; б) 3; в) 0,5; г) 4
а) 4; б) 78; в) 27; г)lg27; .
а) 9; б) 0,5; в) -2; г) 2;
а) 7; б) 2; в) -7; г) -2
а) 15; б) 4; в) -15; г) 2 a)
а) 3 a+ 2b; б) 1 + a +2 b; в) 1+ a + b; г) a – b
а) -2; б) -1; в) 2 г) 1 |
а) 3; б) 32 в) 4; г) 16
а) 3; б) 0; в) 2; г) 1
а)16; б) 2; в) lg16; г) 4.
а) 16; б) 4; в) 8; г) 2
а) 1; б) 4; в) 2; г) 9; 7. Вычислить а) 7; б) 2; в) -2; г) -7
a) 0,5; б) 2; в) 1; г)
а) 2 a+ 2b;б) 2( a + b); в) 1 + 2a +b; г) 1+a + 2b
а) 2; б) 1; в) -2 г) -1 |
а) 3; б) -3; в) 9; г) -9
а) -1; б) 3 в) 1; г) 5
а) 9; б)
а) 1; б) 4; в) 3; г) 0,5
а) 3; б) 4; в) 5; г) 17
а) 15; б) 4; в) 8; г) 2
a) 1; б)
а) 2 a+ b; б) 1 + a + b; в) 3 a + b; г) 2 + a + b
а) -1; б) 1; в) 2; г) -2 |
| Свойства логарифмов | Свойства логарифмов | Свойства логарифмов | Свойства логарифмов |
| Вариант – 9 | Вариант – 10 | Вариант – 11 | Вариант – 12 |
а) 27; б) 9; в) -4; г) 4
а) 2; б) 1; в)
а)16; б) 60; в) lg16; г) 3
а) 6; б) 1; в) 2; г)
а) 13; б) 4; в) 2; г) -13
а) 3a+ 2b;б) 2a+ 3b; в) a - b; г) a + b
а) 2; б) 0,5; в) 1; г) -1 |
а) 13; б) 0,5; в) 4; г) 2
а) 3; б) 0; в) 1; г) 4
а) 4; б) 8; в) lg8; г) 12
а) 10; б) 8; в) 2; г) 4
а) 5; б) 2; в) -5; г) -2
а) 8; б) 3; в) 4; г) 16 a) 2; б) 1; в) 0,5; г)
а) 3 a+ 2b; б) 1 + a + b; в) a + b; г) a - b
а) -2; б) 1; в) 0,5 г) 2 |
а) -4; б) -8; в) 4; г) 8
а) 4; б) 1; в) 2; г) -2
a) 15; б) 2; в) lg15; г) lg210
а) 0,5; б) 4; в) 8; г) 2
а) 4; б) 3; в) 5; г) 16
а) 10; б) 2; в) -2; г) 5
a) 0,5; б) 2; в) 1; г)
а) 1+ a+ 2b; б) 1+ 2a + b; в) 1+ a + b; г) a + b
а) 2; б) 1; в) -2 г) -1 |
а) 2; б) 0,5 в) -2; г) 5
а) 1; б) -5; в) -1; г) 5
а)
а) 3; б) 4; в) 5; г) 0,5
а) 4; б) 3; в) 5; г) 29
а) 9; б) 4; в) 2; г) 3
a) 1; б)
а) 1 +2a+ b; б) 1 + a + b; в) 3 a + b; г) 2 + a + b
а) -1; б) 1; в) 2 г) -2 |
| Основные типы логарифмических уравнений: |
| |
| |
| |
| |
|
| Методы решения логарифмических уравнений. | ||
| Теорема. Уравнения | |
| Пусть Замечание. Потенцирование уравнения может привести к появлению посторонних корней. Пример. Уравнение lg (x2 – 4) = lg (4x – 7) приводит к уравнению – следствию (x2 – 4) = (4x – 7), имеющему корень 1, посторонний для исходного уравнения. | |
| Теорема. Уравнение | 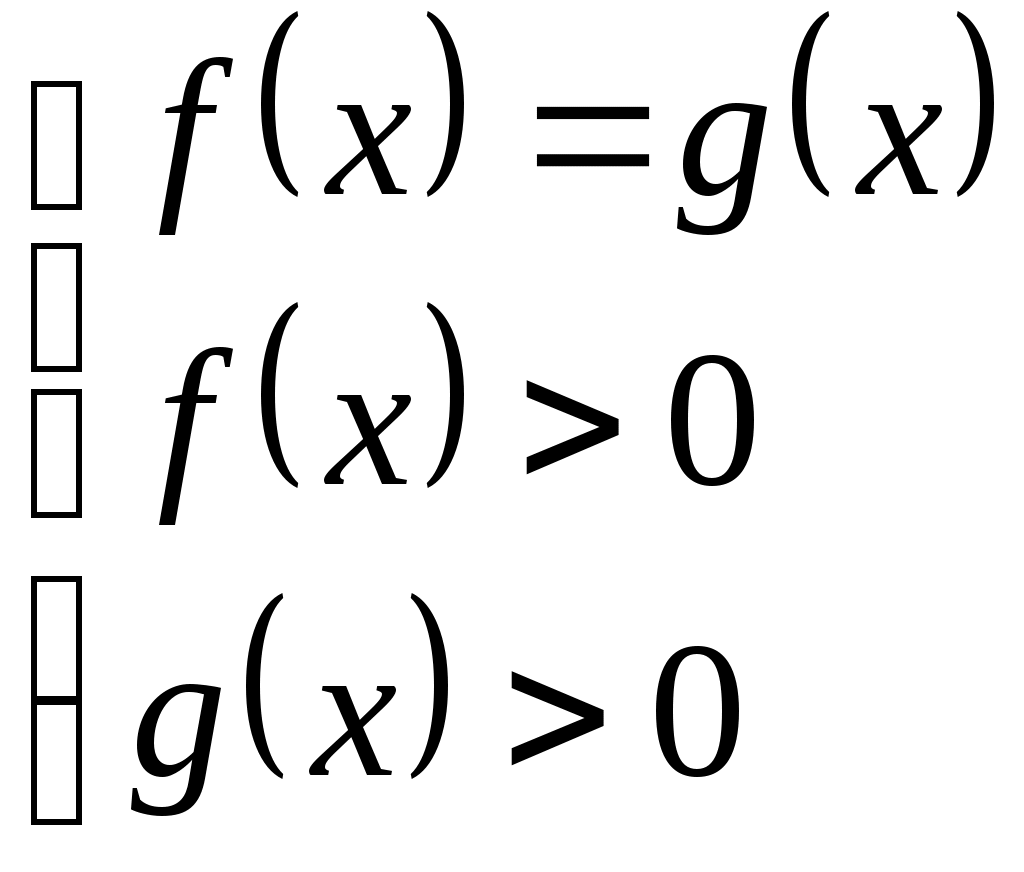 | 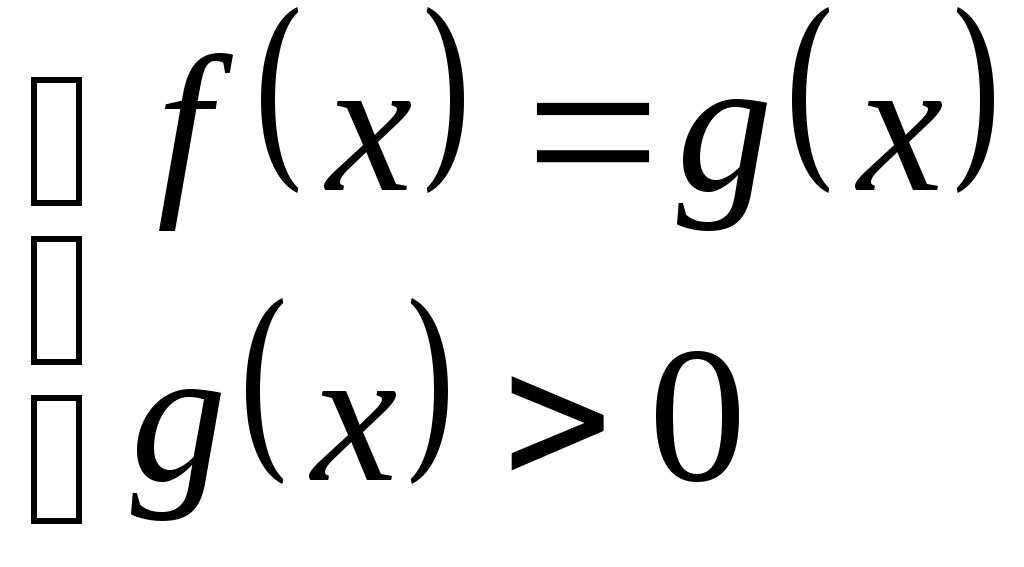 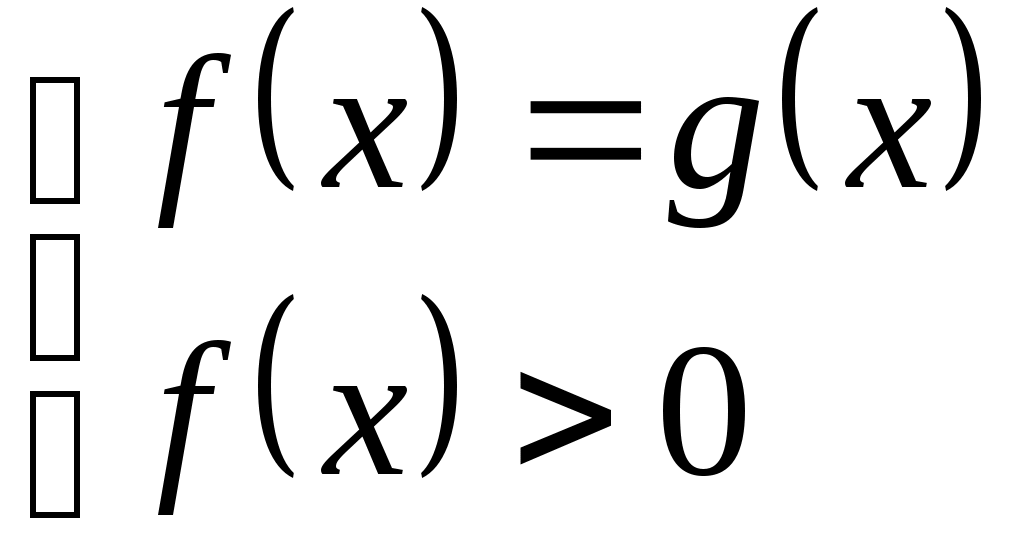 |
| Теорема. Уравнение | 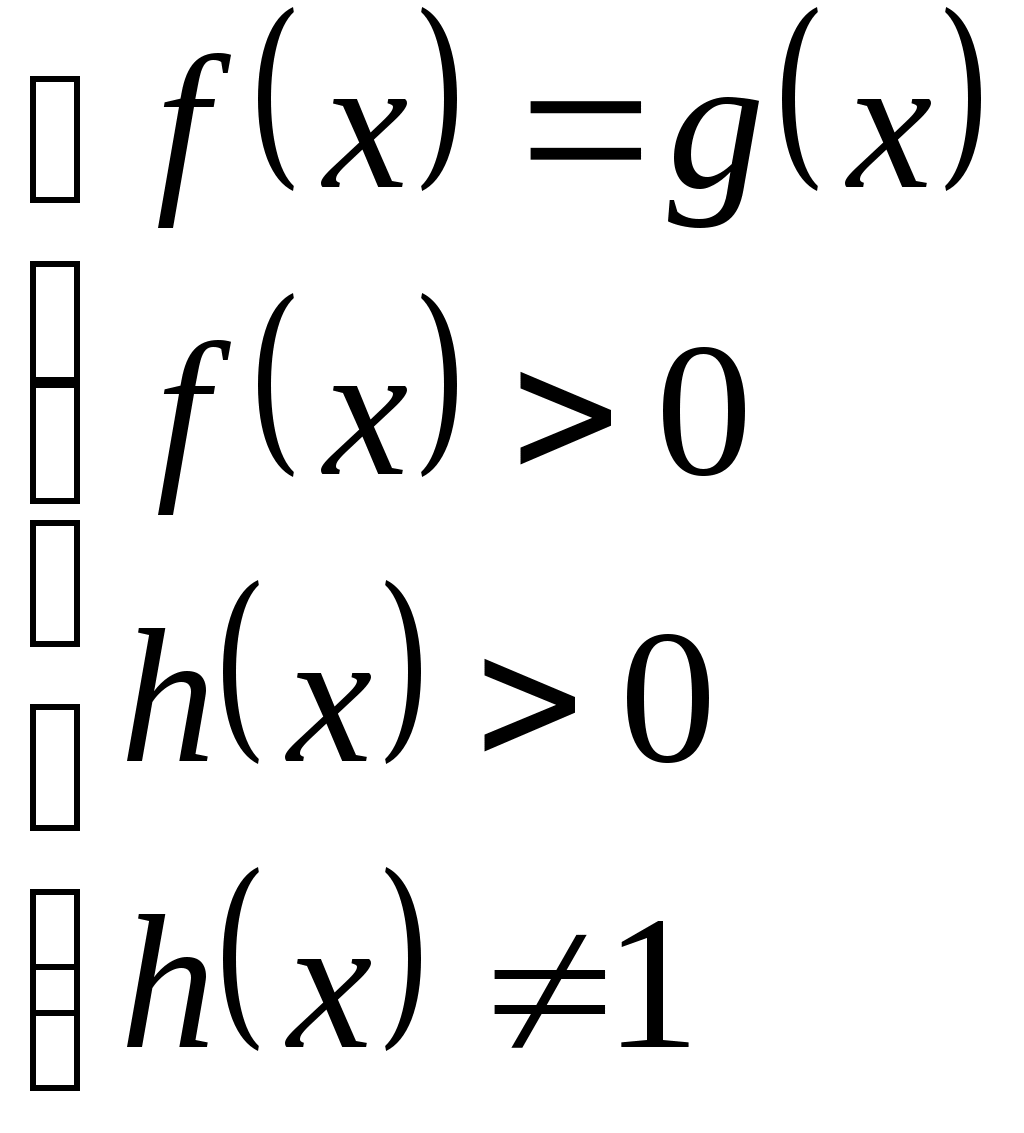 | 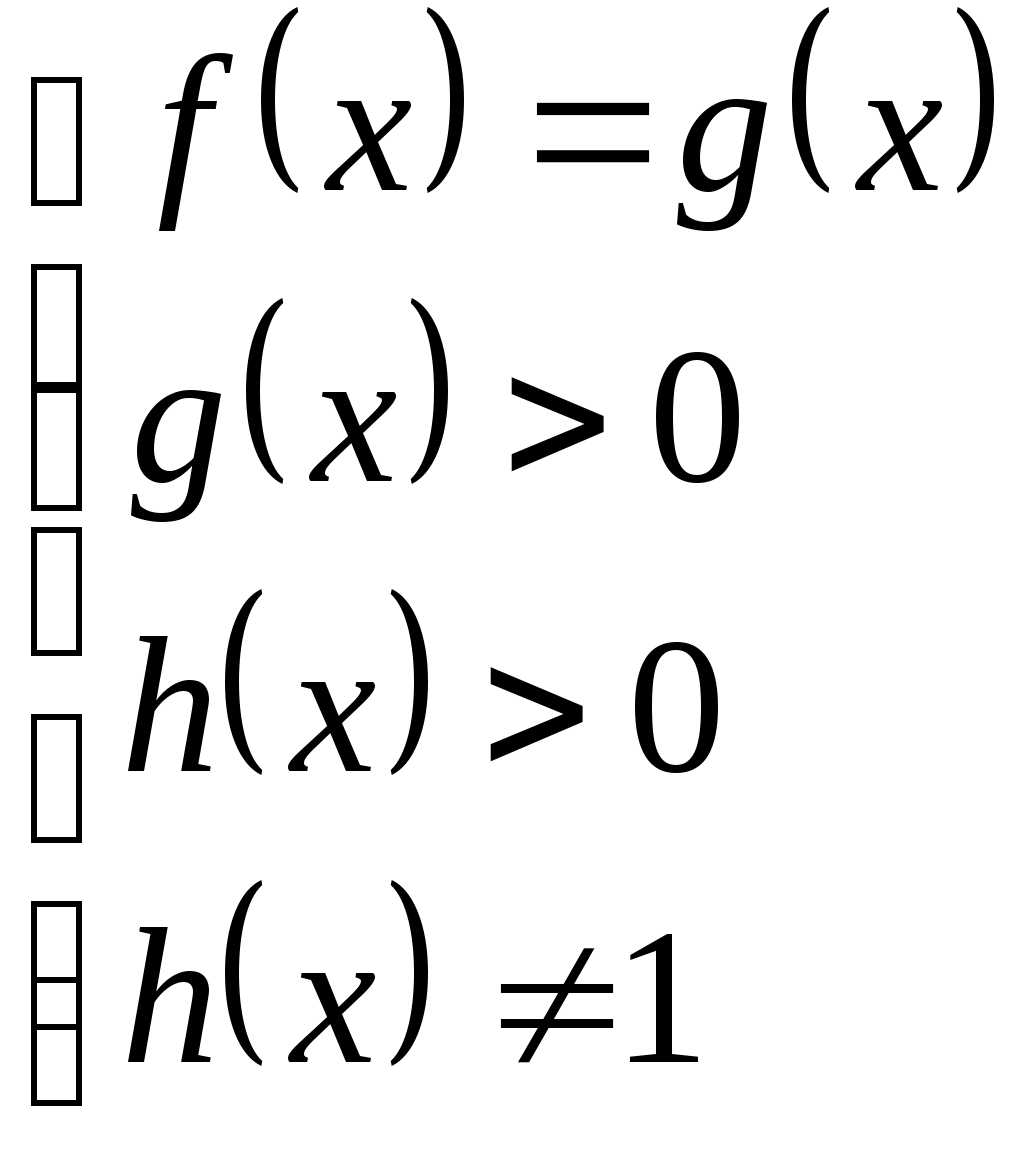 |
| Теорема. Уравнение | 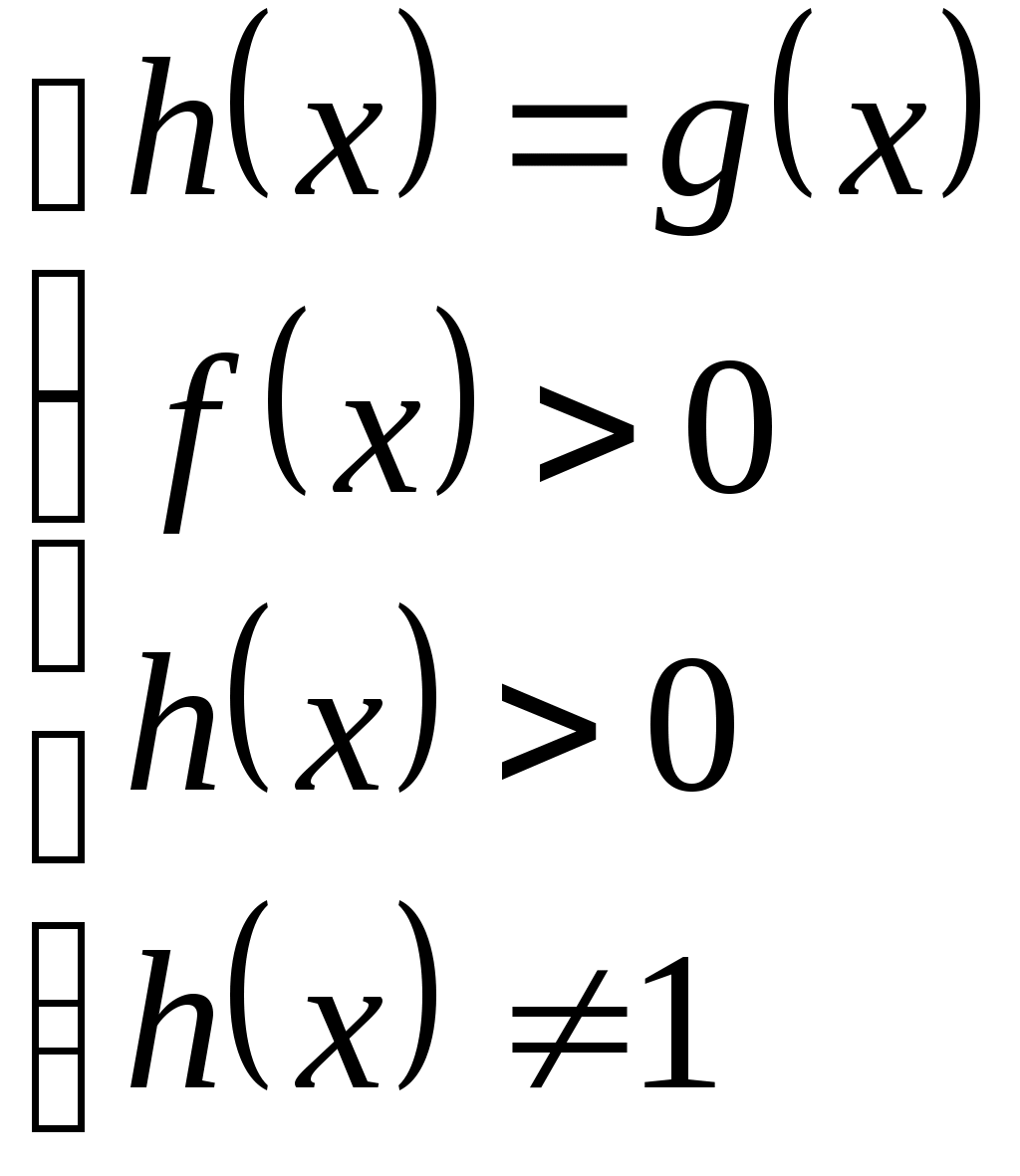 | 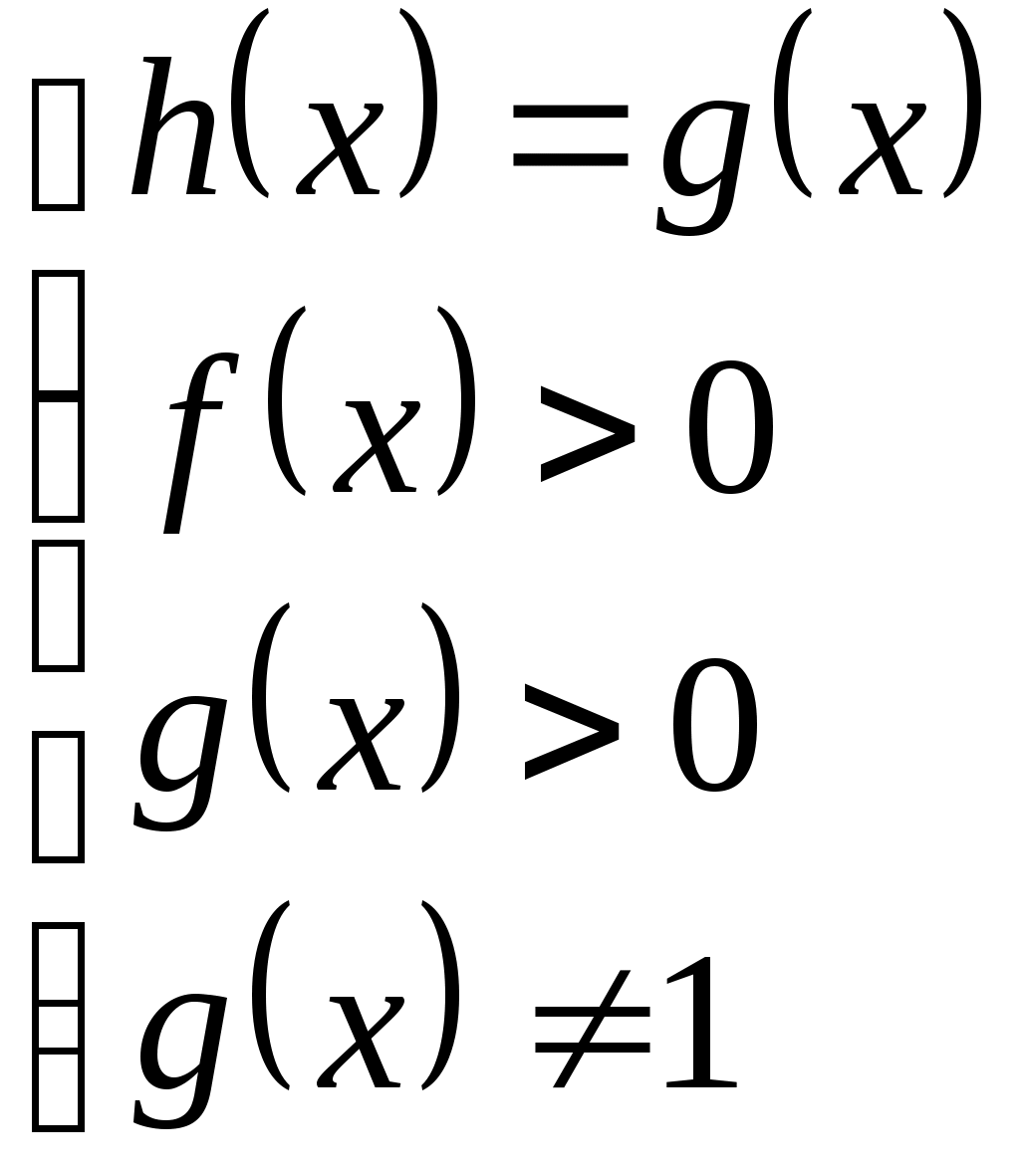 |
| Уравнение Обозначив Отметим, что часто исходное уравнение сводится к одному из указанных типов после некоторых преобразований. | |
| Тема: Решение логарифмических уравнений. | | | Тема: Решение логарифмических уравнений. | ||||||
| I Карточка | I Карточка | ||||||||
| Задание: решите уравнение | Задание: решите уравнение | ||||||||
| Решение: | Решение: | ||||||||
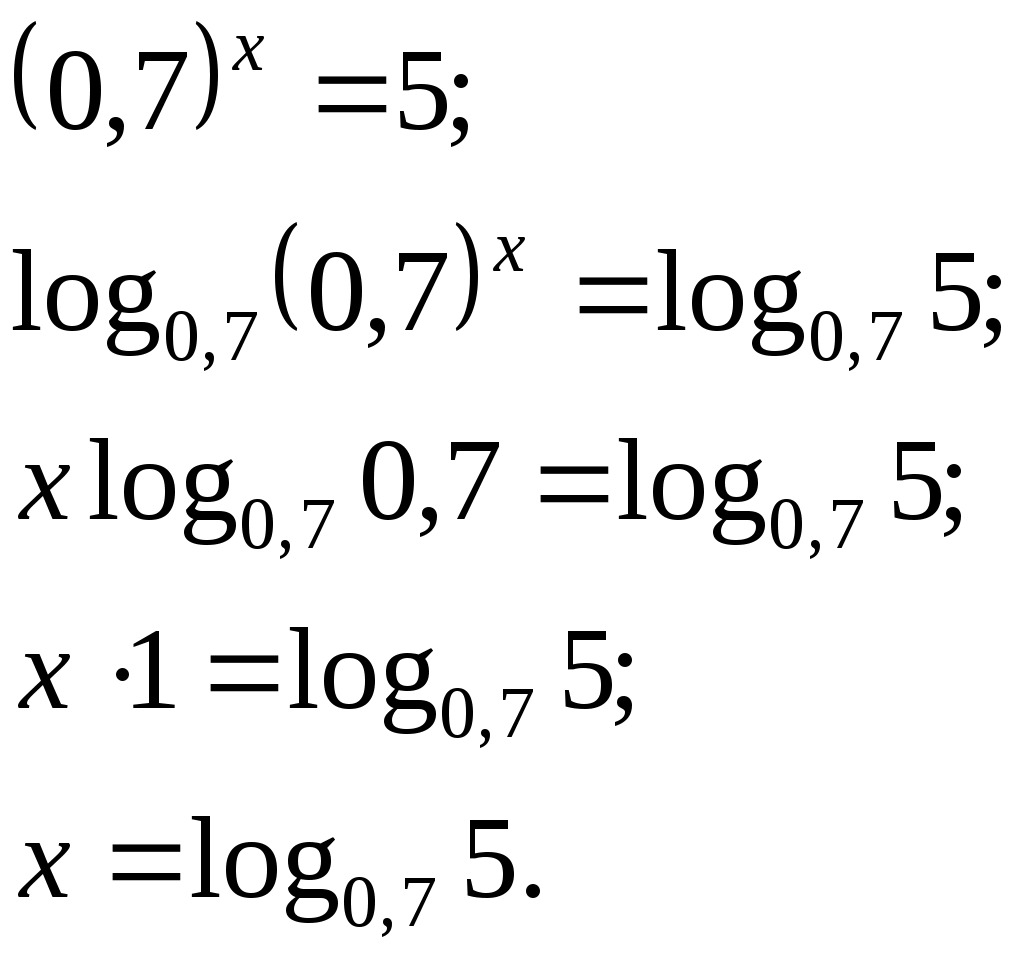 | 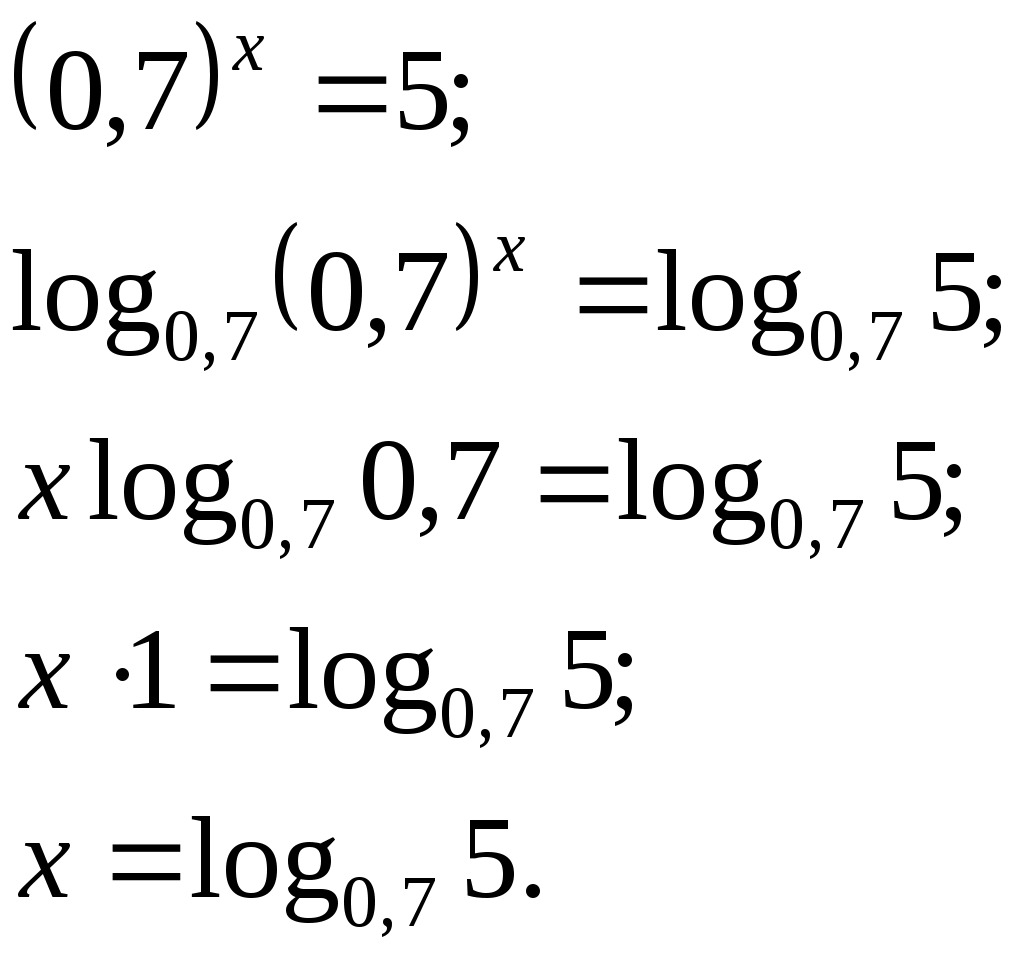 | ||||||||
| Ответ: | Ответ: | ||||||||
| Решите самостоятельно: | Ответы: | Решите самостоятельно: | Ответы: | ||||||
| 1. | | 1. | | 1. | | 1. | | ||
| 2. | | 2. | | 2. | | 2. | | ||
| 3. | | 3. | | 3. | | 3. | | ||
| 4. | | 4. | | 4. | | 4. | | ||