ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 14.04.2024
Просмотров: 26
Скачиваний: 0

ЛАБОРАТОРНАЯ РАБОТА 4
Исследование трехфазной цепи при соединении приемников в треугольник
-
Цель работы.
1.1. Установить соотношение между линейными и фазными токами и напряжениями при различной нагрузке фаз.
1.2.Выявить на опыте влияние обрыва линейного провода на работу трехфазного потребителя.
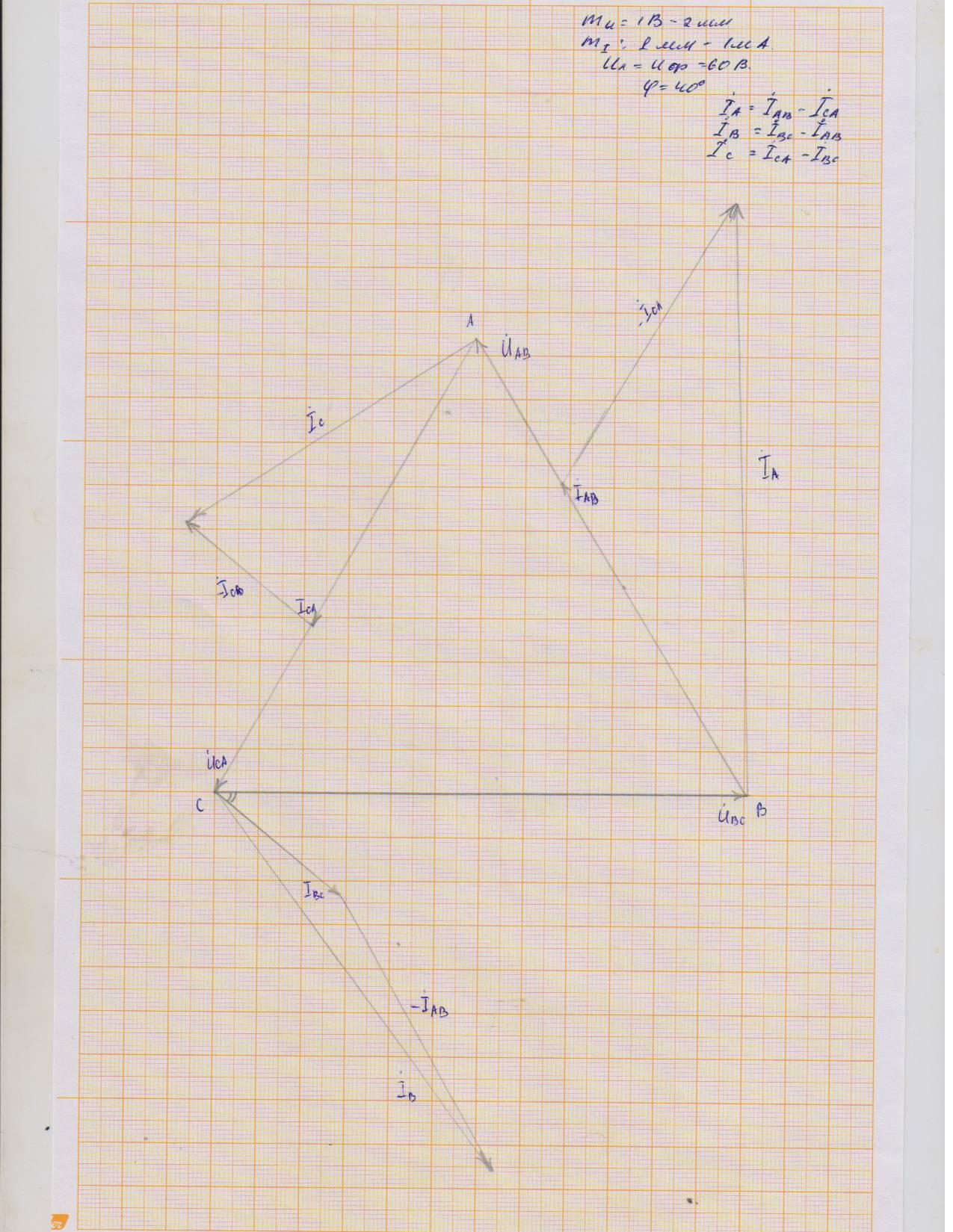
1.3. Построение векторных диаграмм
2. Оборудование.
2.1. Источник энергии переменного тока ~(0÷60) В
2.3. Мультиметр – 4 шт.
2.4. Магазин сопротивлений – 1 шт.
2.5. Набор катушек индуктивности – 1 шт.
2.6. Набор емкостей -1шт.
3. Краткие теоретические сведения
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи бывают несимметричными, очень важно на практике обеспечить независимость режима работы отдельных фаз. Кроме четырехпроводной цепи подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника треугольником. Соединением в треугольник называется соединение, когда конец одной фазы соединяется с началом другой, образуя замкнутый контур. Полученные узлы присоединяют к соответствующим началам фаз генератора линейными проводами (рис. 1).
В треугольник могут соединяться фазы
трансформаторов, электродвигателей,
фазы осветительной нагрузки и т. д. При
соединении фаз приемников с сопротивлениями
![]() в треугольник каждая фаза включается
на линейное напряжение источника.
Поэтому фазные напряжения
в треугольник каждая фаза включается
на линейное напряжение источника.
Поэтому фазные напряжения
![]() равны линейным напряжениям
равны линейным напряжениям
![]() ,
т.е.
,
т.е.
![]() .
.
Фазные токи
![]() определяются по формулам
определяются по формулам
![]() ;
;
![]() ;
;
![]() .
.
Линейные токи
![]() определяются по фазным токам из уравнений,
составленных по первому закону Кирхгофа
для узлов а, в, с (см. рис. 19).
определяются по фазным токам из уравнений,
составленных по первому закону Кирхгофа
для узлов а, в, с (см. рис. 19).

![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
(21)
.
(21)
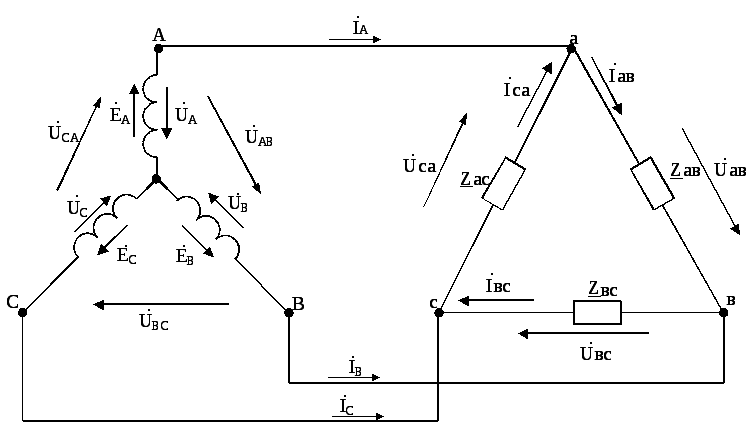
Рис. 1. Схема трехпроводной трехфазной цепи при соединении приемников в треугольник
Из уравнений (28) следует, что любой из
линейных токов равен геометрической
разности токов тех двух фаз нагрузки,
которые соединяются с данным линейным
проводом. Векторы линейных токов
![]() можно определить из векторной диаграммы,
построенной на основании уравнений
(21), для чисто активной нагрузки, например,
осветительной (рис. 20).
можно определить из векторной диаграммы,
построенной на основании уравнений
(21), для чисто активной нагрузки, например,
осветительной (рис. 20).
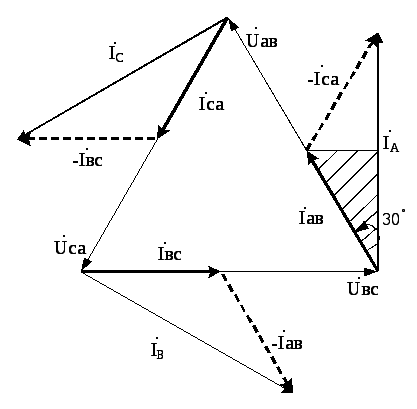
При симметричной нагрузке
|
Рис. 20. Векторная топографическая диаграмма напряжений и токов для симметричной нагрузки |
При этом линейный
|
 При
несимметричной нагрузке - при
изменении сопротивления одной из фаз,
режим работы других фаз останется
неизменным, так как сохраняется
постоянство напряжений на фазах нагрузки,
что является важной особенностью
соединения фаз приемника треугольником.
Поэтому схему соединения треугольником
используют для включения несимметричных
однофазных приемников, например,
осветительных приборов в трехпроводную
осветительную сеть.
При
несимметричной нагрузке - при
изменении сопротивления одной из фаз,
режим работы других фаз останется
неизменным, так как сохраняется
постоянство напряжений на фазах нагрузки,
что является важной особенностью
соединения фаз приемника треугольником.
Поэтому схему соединения треугольником
используют для включения несимметричных
однофазных приемников, например,
осветительных приборов в трехпроводную
осветительную сеть.
В зависимости от условий работы нагрузки целесообразно изменять способ соединения фаз – переключать со звезды на треугольник и обратно, при этом линейный ток нагрузки изменяется в три раза.
![]() ;
;
![]() ,
тогда отношение
,
тогда отношение
![]() ,
т. е.
,
т. е.
![]() .
.
Активную мощность каждой фазы можно определить по формуле
![]() ,
,
а всей цепи – как
![]() .
.
Активная мощность симметричного
трехфазного приемника, как и при
соединении фаз звездой:
![]() .
.
Реактивная мощность каждой фазы определяется по формуле
![]() .
.
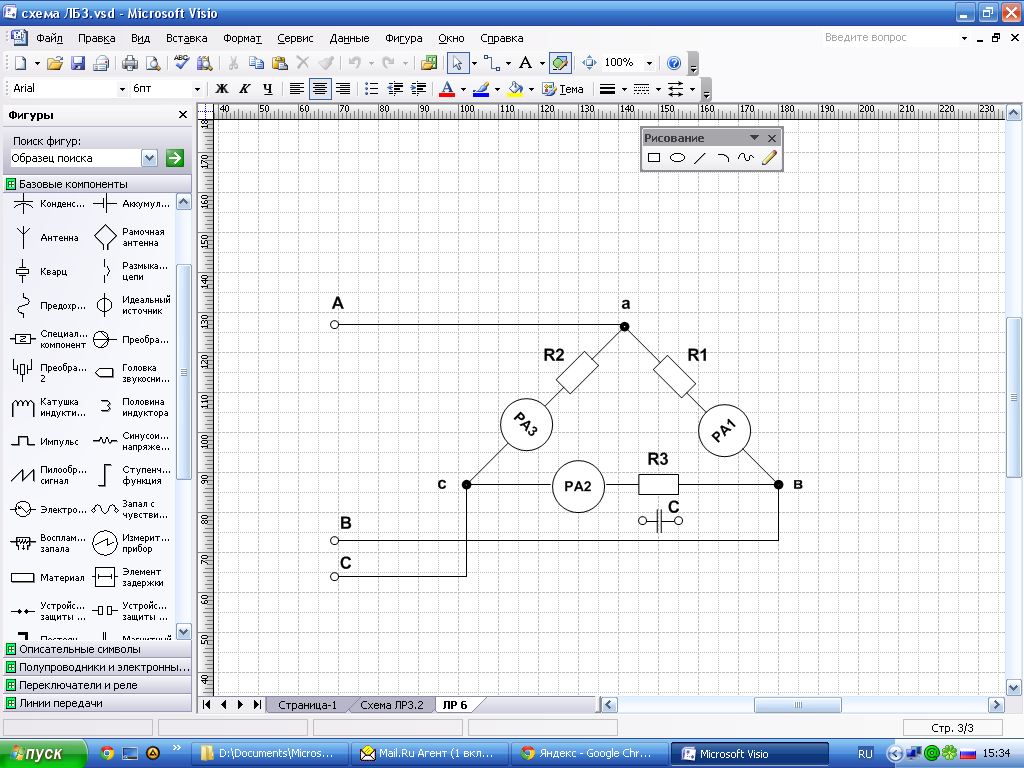

R1=750 Oм
R2=1000 Oм
R3=1200 Oм
С=3мкФ
UA=60В
![]()
IA+ICA=IAB; IA=IAВ-IAС;
IВ+IAВ-IB0=0; IB=IВC-IAB;
IC+IВC-ICA=0; IC=ICA-ICB;
IA=![]() IAВ
IAВ
IВ=![]() IВC
IВC
IC=![]() IAC
IAC
IA=139.8 (мА)
IВ=83,9 (мА)
IC=112 (мА)