ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 119
Скачиваний: 0
Строим точечный график и подбираем угловой коээфициент аппроксимирующей прямой:
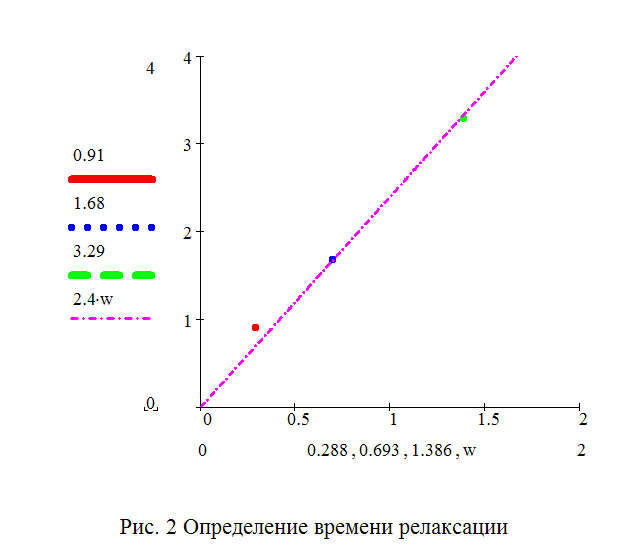
Отсюда хорошо
видно, что
![]() с.
с.
Тогда соответствующая формула (5) для определения вязкости дает результат:
![]() =4,710-5
(Пас),
=4,710-5
(Пас),
что хорошо согласутся с результатами предыдущих вычислений вязкости (без рассмотрения времени релаксации).

Тогда встает вопрос: Скорее всего результат, не схожий с табличными данными, обусловлен не погрешностями отдельных прямых измерений и погрешностью определения давления, обусловливающего протекание воздуха через капилляр, а чем-то иным. Например:
1) самим методом Пуазейля, например, невыполнимостью условий его применимости в используемой установке;
2) несовершенством самой установки (влияние соединительного шланга и пр.);
3) или тем, что найденные нами данные о вязкости воздуха не верны;
4) или тем, что в лаборатории МКТ ЕГУ им. И.А. Бунина вовсе НЕ воздух, а ИНОЙ газ!!!
А что скажите вы??????????????????
Оценка погрешности косвенного измерения
Способ №1.1
![]()
Погрешности прямых однократных измерений аргументов:
|
r, м |
(h1+ h2), м |
t, c |
H, м |
R, м |
L, м |
, Пас |
|
1
деление =
|
610-3 |
0,2 |
610-3 |
510-5 |
310-3 |
|
![]() частные производные
и их значения по данным опыта:
частные производные
и их значения по данным опыта:
![]() =0,656
=0,656
![]() =0,656210-5=1,31310-5;
=0,656210-5=1,31310-5;
![]() =0,00016
=0,00016
![]() =0,09810-5;
=0,09810-5;
![]() =0,0000029
=0,0000029
![]() =0,58610-5;
=0,58610-5;
![]() =-0,000492
=-0,000492
![]() =-0,295410-5;
=-0,295410-5;
![]() =0,042
=0,042
![]() =-0,209510-5;
=-0,209510-5;
![]() =0,000268
=0,000268
![]() =-0,0802610-5.
=-0,0802610-5.
Находим погрешность, обусловленную неточностью измерений аргументов:
![]() (Пас)
(Пас)
Видно, что даже одна только эта погрешность сравнима с истинным значением искомой вязкости.
Кроме этой погрешности результат отягощен методической погрешностью, обусловленной изменением давления в ходе опыта. А также, возможно, не соблюдением условий применения формулы Пуазейля.
Максимальный вклад в погрешность среди аргументов дает величина внутреннего радиуса капилляра и значение времени протекания воздуха через капилляр.
Субъективные погрешности учитывались при задании абсолютных погрешностей аргументов.
С учетом этого в
качестве меры ширины доверительного
интервала выберем удвоенное значение
![]() ,
т.е. примем за абсолютную погрешность:
,
т.е. примем за абсолютную погрешность:
=![]() Пас.
Пас.
Тогда полученный результат придется округлить до целых порядка 10-5.
Относительная погрешность:
![]()
Результат:
= (53)10-5
(Пас),
![]() ,
Р=0,95.
,
Р=0,95.
Выводы:
1) применение метода Пуазейля для измерения коэффициента вязкости воздуха на имеющейся в лаборатории МКТ ЕГУ установке (с учетом ее текущего состояния) позволяет точно определить порядок величины. Ввиду большой систематической погрешности, в частности методической, нельзя повысить точность результата за счет многократности измерений.
2) значение вязкости, полученное на основе определения времени релаксации (уровень №2), соответствует результату, полученному первым способом (уровень №1).
Итоги и размышления. Большая погрешность может объясняться несколькими различными факторами:
-
Погрешностью метода (изменение давления с течением времени. Надо подумать, как можно обеспечить примерное постоянство давления).
-
Большим числом аргументов, значения которых 1) определяются не достаточно точно и 2) взаимосвязаны (погрешность времени связана с погрешностью разности высот уровней жидкости в манометре).
-
Не идеальностью отдельных элементов установки (не ровная трубка, не одинаковые сечения колен манометра и др.).
-
Невозможностью осуществить рандомизацию.
-
И чем-нибудь еще!
Достижения по улучшению методики проведения работы и качества прямых измерений:
_________В ходе повторных испытаний обнаружен промах в определении внутреннего радиуса r капилляра. Ошибка устранена._Примененная методика «отсечения хвоста» также дает хороший результат в сравнении с результатом уровня №1.______ ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Работу выполняли: _______________________________________________
_______________________________________________
_______________________________________________
_______________________________________________
Молодцы!!! «О нас еще узнают!!!»
Приложения
Экспериментальная действительность данной работы в картинках

Определение радиуса капилляра с помощью катетометра.