Файл: Физика.doc

1)Основные кинематические величины

Перемещение— векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:

.

Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.

Средняя скорость— векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:

.

Мгновенная скорость— векторная физическая величина, равная первойпроизводнойот радиус-вектора по времени:

.

Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:

.

Единица измерения скорости в системе СИ—м/с, в системеСГС— см/с. Мгновенная скорость всегда направлена по касательной к траектории.

Мгновенное ускорение— векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:

.

Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить посопутствующему базису: на вектор нормального и тангенциального ускорения:

.

Здесь — единичныйвектор нормали,— единичный вектор касательной. Величинаназываетсянормальным ускорениеми характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость ирадиус кривизнытраектории:

---

.

В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.

Величина называетсятангенциальным ускорениеми характеризует величину изменения модуля скорости:

.

2) Первый закон Ньютона

     1-й закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет его из этого  состояния.

     -    I закон  Ньютона

 

       Этот закон называют законом инерции. Инерция - способность тела сохранять скорость. Движение по инерции - движение с постоянной скоростью.

       1-й закон Ньютона выполняется не во всех системах отсчета.  Системы отсчета, в которых выполняется 1-й закон Ньютона, называются инерциальными. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.

П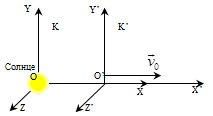римером инерциальной системы отсчета может служить гелиоцентрическая система отсчета, т. е. система отсчета, связанная с  Солнцем.

Любая система отсчета, движущаяся относительно гелиоцентрической равномерно и прямолинейно будет являться инерциальной.

Лабораторная система отсчета, оси координат которой жестко связаны с Землей, неинерциальная из-за суточного вращения Земли. Однако вращение Земли происходит очень медленно с а=0,034 м/с², и поэтому в большинстве задач лабораторную систему отсчета можно приближенно считать инерциальной.

Содержание 1-го з. Н. сводится к двум утверждениям:

1) все тела обладают свойством инертности;

2) существуют инерциальные системы отсчета.

Инерциальные системы отсчета играют особую роль не только в механике, но и в других  разделах физики, т. к. согласно принципу относительности Эйнштейна математическая запись любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчета.

---

 3) Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.

Примером такого движения является движение тела, брошенного под углом  к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением , направленным вертикально вниз.

При равноускоренном движении по прямой скорость тела определяется формулой:

Зная, что , найдём формулу для определения координаты x:

Примечание. Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора  и  противонаправлены). Равнозамедленное движение также является равноускоренным.

4) Свобо́дное падéние — равноускоренное движение под действием силы тяжести. На поверхности Земли, на уровне моря, ускорение свободного падения меняется от 9,81 м/с² на полюсах до 9,78 м/с² на экваторе.

В частности парашютист, в течение нескольких первых секунд прыжка, находится практически в свободном падении.

Свободное падение возможно на поверхность любого тела, обладающего достаточной массой (планеты и их спутники, звезды, и т. п.).

На объекте, находящемся в состоянии свободного падения, все физические процессы протекают так же, как и в состоянии невесомости. Это используется, например, при тренировке космонавтов: самолёт с космонавтами набирает большую высоту и пикирует, в течение нескольких минут находясь в состоянии свободного падения, при этом космонавты и экипаж испытывают состояние невесомости.

5) Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

---

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; — полная фаза колебаний, — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )

6) 2-й закон Ньютона.

Ускорение, полученное телом в результате взаимодействия, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела:. Выражение справедливо для любых сил любой природы.

7) Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

---

, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения^[1]. Период малых собственных колебанийматематического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

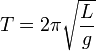
и не зависит^[2] от амплитуды колебаний и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

8) 3-й закон Ньютона.

Силы, с которыми два тела действуют друг на друга, равны по величине, направлены в противоположные стороны F₁₂ = - F₂₁.

F₁₂ - сила, действующая со стороны второго тела на первое, приложена к первому телу, F₂₁ - сила, действующая на второе тело со стороны первого, приложена ко второму телу

9) Момент импульса  материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы.

Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:

---