Файл: Физика.doc

Микроканоническое распределение Гиббса — распределение вероятностей различных состояний замкнутой макроскопической системы, т. е. системы, не взаимодействующей с окружающими телами и имеющей постоянную энергию. Подобная система в действительности не может быть получена и является идеализированной. Ее состояния являются вырожденными: каждому значению энергии могут соответствовать различные состояния. Кратностью вырождения данного состояния называется число состояний, обладающих энергией .

Микроканоническое распределение основано на предположении о равной вероятности различных состояний, имеющих одну и ту же энергию. При изображении состояния системы в фазовом пространстве каждому состоянию соответствует ячейка (клетка), и их совокупность с заданной энергией образует некоторую поверхность .
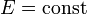Макроскопические системы, которые могут в течение достаточно большого времени пребывать в любом состоянии с данной энергией, называются эргодическими. Предположение, лежащее в основе микроканонического распределения, означает, что изобразительная точка в фазовом пространстве с равной вероятностью располагается в любой ячейке фазового пространства на поверхности .
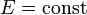Для эргодических систем, состояния которых с данной 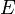энергией равновероятны, справедливо утверждение: если макроскопическая система в некоторый момент времени находится в данном состоянии с энергией 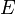, то с течением времени она будет самопроизвольно переходить в любые другие состояния с той же энергией и находиться в каждом из них (в среднем) одинаково долго.
Вероятность 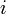-го состояния системы 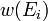выражается микроканоническим распределением Гиббса:

Коэффициент пропорциональности определяется из условия вероятностной нормировки

Микроканоническое распределение Гиббса лежит в основе канонического распределения Гиббса.

Каноническое распределение Править

Каноническое распределение Гиббса — распределение вероятностей различных возможных состояний некоторой квазизамкнутой подсистемы, т. е. некоторой части замкнутой макроскопической системы. Подсистема называется квазизамкнутой, если ее собственная энергия в среднем велика по сравнению с энергией ее взаимодействия с остальными частями замкнутой системы (называемыми термостатом). Например, каждая молекула идеального газа при не слишком низких температурах является квазизамкиутой подсистемой. Ее собственная кинетическая энергия в среднем намного превышает энергию ее взаимодействия с другими молекулами газа (термостатом).

Взаимодействие подсистемы с термостатом приводит к изменению ее состояний: она может переходить как в состояния с первоначальной энергией, так и в состояния с другими значениями энергии. При последних переходах подсистема обменивается энергией с термостатом, увеличивая или уменьшая свою энергию.
Вероятность состояния подсистемы зависит только от ее энергии. Согласно дискретному (квантовому) каноническому распределению Гиббса

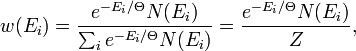
где — вероятность пребывания квазизамкиутой подсистемы в состоянии с энергией — кратность «вырождения» (кратность состояния с энергией ), — модуль канонического распределения, или статистическая температура — температура, выраженная в энергетических единицах. Универсальным коэффициентом пропорциональности, переводящим статистическую температуру из эргов в градусы, является постоянная Больцмана :

Величина называется суммой по состояниям, или статистической суммой.

Для систем, энергия состояний которых изменяется квазинепрерывно, т. е. расстояния между энергетическими уровнями которых малы сравнительно с 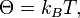дискретное (квантовое) распределение Гиббса переходит в классическое каноническое распределение:

где — число различных состояний, отвечающих интервалу энергий от до ,

— интеграл состояний или фазовый интеграл. Для системы тождественных частиц

где — элемент фазового объема, — постоянная Планка, — число степеней свободы системы, а интегрирование проводится по всему фазовому пространству данной системы. Интеграл состоянии истатистическая сумма связаны со свободной энергией системы соотношением

Для подсистемы с большим числом частиц каноническое распределение Гиббса имеет резкий максимум. Такая подсистема наибольшую часть времени находится в наиболее вероятном состоянии с соответствующей ему энергией. Если подсистемой является одна молекула идеального газа, то каноническое распределение Гиббса переходит в распределение Больцмана. Каноническое распределение Гиббса применяется при отыскании среднего значения 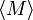физической величины 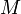, характеризующей состояние системы и зависящей от ее энергии:

При непрерывном изменении состояний

Вычисление 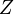позволяет отыскать термодинамические функции и уравнение состояния данной системы.

35) Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе.

Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физике ионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

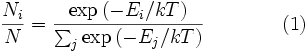где является числом молекул имеющих энергию при температуре системы , является общим числом молекул в системе и — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем , обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.