ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.04.2024
Просмотров: 107
Скачиваний: 1
27) Кеплера законы
Кеплера законы, три закона движения планет, открытые И. Кеплером в начале 17 в. Основной труд Кеплера "Новая астрономия", напечатанный в 1609, содержал два первых закона. Третий закон был открыт позднее: в 3-й главе 5-й книги "Гармония Мира" (1619) Кеплер отметил, что идея нового закона блеснула у него внезапно 8 марта 1618 года, а 15 мая он закончил все необходимые вычисления, которые показали, что закон верен. В дальнейшем К. з. уточнялись и окончательно получили следующую формулировку.
Первый К. з. В невозмущённом движении (т. е. в задаче двух тел) орбита движущейся точки есть кривая второго порядка, в одном из фокусов которой находится центр силы притяжения. Таким образом, орбита материальной точки в невозмущённом движении — это некоторое коническое сечение, то есть окружность, эллипс, парабола или гипербола. Второй К. з. В невозмущенном движении площадь, описываемая радиус-вектором движущейся точки, изменяется пропорционально времени. Первые два К. з. имеют место только для невозмущенного движения, происходящего под действием силы притяжения, обратно пропорциональной квадрату расстояния до центра силы. Третий К. з. В невозмущенном эллиптическом движении двух материальных точек произведение квадратов времен обращения на суммы масс центральной и движущейся точек как кубы больших полуосей их орбит, т. е.
,
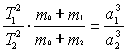где Т1 и Т2 — периоды обращения двух точек, m1 и m2 — их массы, m0 — масса центральной точки, a1 и а2 — большие полуоси орбит точек. Пренебрегая массами планет по сравнению с массой Солнца, получаем третий К. з. в его первоначальной форме: квадраты периодов обращений двух планет вокруг Солнца относятся как кубы больших полуосей их эллиптических орбит. Третий К. з. может быть применен только для случая эллиптических орбит, а поэтому не имеет такого общего значения, как два первых закона. Однако, будучи применен к планетам, спутникам планет, компонентам двойных звёзд, движущимся по эллиптическим орбитам, он позволяет определить некоторые характеристики небесных светил. Так, на основании третьего К. з. возможно подсчитать массы планет, принимая массу Солнца m0 = 1. Зная из наблюдений период обращения одного компонента двойной звезды относительно другого и измерив её параллакс, можно найти сумму их масс. Если параллаксы звёзд неизвестны, то на основании допущения, что массы компонентов соответствуют их физическим особенностям, по третьему К. з. можно вычислить расстояния до звёзд (это так называемы динамические параллаксы звёзд).
Открыв первые два закона, Кеплер составил основанные на них таблицы движения планет, опубликованные в 1627 под названием "Рудольфовых таблиц". Эти таблицы по своей точности далеко превзошли все прежние, ими пользовались в практической астрономии на протяжении 17 и 18 вв. Успех Кеплера в объяснении движения планет обусловлен новым методологическим подходом к решению вопроса: впервые в истории астрономии была сделана попытка определить планетные орбиты непосредственно из наблюдений.
Уже Кеплеру было ясно, что открытые им законы не являются совершенно строгими. Если для планет они выполняются с большой точностью, то для того, чтобы представить движение Луны, оказалось необходимым ввести эллипс с вращающейся линией апсид и добавить неравенства, называемые эвекцией и вариацией. Эти неравенства были открыты эмпирически ещё Птолемеем во 2 в. (эвекция) и Т. Браге в 16 в. (вариация) и объяснены только после открытия в 17 в. И. Ньютоном закона всемирного тяготения (см. Ньютона закон тяготения). К. з., найденные из наблюдений, были выведены Ньютоном как строгое решение задачи двух тел.
28) ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- ф-ция
для описания распределения вероятностей
значений случайной
величины. Для
всех возможных значений х
(
<х<
)случайной
величины x Ф. р.
где Р{x<=х}- вероятность
события x<= х. Ф.
p. Fx(x)
монотонно не убывает, она непрерывна
справа: Fx(x
+0)
==
,
и имеет пределы 
=1.
Если x, дискретна, то Ф. р. является
ступенчатой, увеличиваясь скачкообразно
в каждой точке xk на
величину P(x =
xk ). В
случае непрерывной случайной величины
x вероятность каждого возможного
значения х равна Р(x =
х )и
Ф. р. становится непрерывной. Если она
ещё и дифференцируема, то вводится P(x)
= dF(x)/dx - плотность
распределения вероятности, называемая
также п л о т н о с т ь ю в е р о я т н о с т
и или д и ф ф е р е н ц и а л ь н о й Ф. р.
Индекс x часто опускают.
В более общем случае Ф. р. задаётся не на прямой х, а на множестве значений x1, ..., xN случайных величин x1, ..., xN с учётом явной зависимости Ф. р. от времени.
30) ЛИУВИЛЛЯ ТЕОРЕМА - теорема механики, согласно к-рой фазовый объём системы, подчиняющейся ур-ниям механики в форме Гамильтона, остаётся постоянным при движении системы. Теорема установлена Ж. Лиувиллем (J. Liouville) в 1838.
Состояние
механич. системы, определяемое обобщёнными
координатами q=(q1, q2, .....,
qN)и
канонически сопряжёнными обобщёнными
импульсами P = (P1, Р2,
......, pN)
(N -
число степеней свободы системы), можно
изобразить точкой в пространстве 2Nизмерений
(фазовом
пространстве).
Изменение состояния системы во времени
представляется как движение такой
фазовой точки в 2N-мерном
фазовом пространстве. Если в нач. момент
времени фазовые точки 
непрерывно
заполняли нек-рую область 
в
фазовом пространстве, а с течением
времени перешли в др. область
этого
пространства, то, согласно Л. т.,
соответствующие фазовые объёмы (2N-мерные
интегралы) равны между собой:
Т. о.,
движение точек, изображающих 
состояния
системы в фазовом пространстве, подобно
движению несжимаемой жидкости.
Л. т.
является следствием того,
что якобиан преобразования
от переменных 
к
переменным р,
q (т.
е. якобиан канонич. преобразования) в
силу Гамильтона
уравнений равен
1:
поэтому
Л. т. позволяет ввести ф-цию распределения для плотности вероятности нахождения фазовых точек р, q в элементе фазового объёма dpdq и вывести для неё Лиувилля уравнение, являющееся основой статистич. физики.
31) Эне́ргия (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая системаявляется замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».
32) Энтропи́я (от др.-греч. ἐντροπία — поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, встатистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феноменаальтернативности истории (инвариантности и вариативности исторического процесса).
Энтропия в информатике — степень неполноты, неопределённости знаний.
Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
,
где 
—
приращение энтропии; 
—
минимальная теплота, подведенная к
системе; T — абсолютная температура
процесса;
33) Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая приходящуюся на однустепень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состоянии термодинамического равновесия.В Международной системе единиц (СИ) термодинамическая температура используется в качестве одной из семи основных физических величин, входящих в Международную систему величин (англ. International System of Quantities, ISQ), а её единицей является кельвин, представляющий собой, соответственно, одну из семи основных единиц СИ[2]. Кроме термодинамической температуры в СИ используется температура Цельсия, её единицей является градус Цельсия, входящий в состав производных единиц СИ, имеющих специальные наименования и обозначения, и по размеру равный кельвину[3]. На практике часто применяют градусы Цельсия из-за исторической привязки к важным характеристикам воды — температуре таяния льда (0 °C) и температуре кипения (100 °C). Это удобно, так как большинство климатических процессов, процессов в живой природе и т. д. связаны с этим диапазоном. Изменение температуры на один градус Цельсия тождественно изменению температуры на один кельвин. Поэтому после введения в 1967 г. нового определения кельвина, температура кипения воды перестала играть роль неизменной реперной точки и, как показывают точные измерения, она уже не равна 100 °C, а близка к 99,975 °C[4].
Существуют также шкала Фаренгейта и некоторые другие.
34) Распределение Гиббса — распределение вероятностей различных состояний термодинамической системы; впервые введено Дж. У. Гиббсом в 1878; различают микроканоническое и каноническое распределение Гиббса.