1. Метод прогонки решения разностных уравнений.

Пусть требуется решить стационарную краевую задачу математической физики, то есть когда искомая функция зависит лишь от одной пространственной координаты и не зависит от . Пусть краевая задача имеет вид:

Решение поставленной задачи ищем на равномерной сетке

Производные аппроксимируем конечно разностными формулами (то есть находим приближенное значение, путем выбора вспомогательной функции похожей на данную на определенном отрезке(рассматриваемом))

Таким образом (1)-(2) сведется к сист лин алг урав

где - заданные краевые условия.

Очевидно, что система (5) имеет трехдиагональную матрицу, матрицу, так как каждое уравнение содержит лишь 3 соседних неизвестных.

Суть метода: решение отыскиваем в виде

где - пока неизвестные коэффициенты, называемые прогоночными коэффициентами.

Если заменить в (8) j на j-1 и подставить:

в уравнение (5), то оно преобразуется к виду:

Сравнивая теперь (8) и (10) получаем рекуррентные формулы для прогоночных коэффициентов

Применяя (8) к j=0 и используя краевые условия, находим

.

Таким образом решение складывается из двух этапов

---

-прямой ход: вычисляются прогоночные коэффциенты по рекуррентным формулам (11) с начальными значениями (12).

-обратный ход вычисляются значения функций.

Задача 1.1. Дана краевая задача

Соответствующая ей система разностных уравнений имеет вид:

, ,

,

.

Решить эту систему методом прогонки для .

Решение: суть метода рассказывается чуть выше

) – общий вид уравнения,

- уравнения из условия задачи.

Перепишем его в виде

Используем равномерную сетку (то есть шаг изменения переменных постоянный)

Пусть N=4, тогда h=1/4, , j=1…4

Причем:

- граничная точка

- внутренние точки

- граничная точка

Используя трехточечную разностную схему, получим СЛАУ из трех уравнений

---

где

Имеем прямой ход метода прогонки и прогоночные коэффициенты

Прямой ход

и так далее до получаем, что

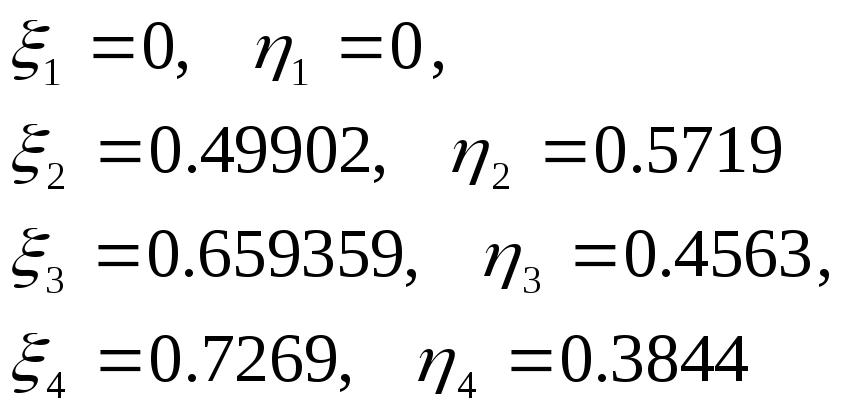
Обратный ход:

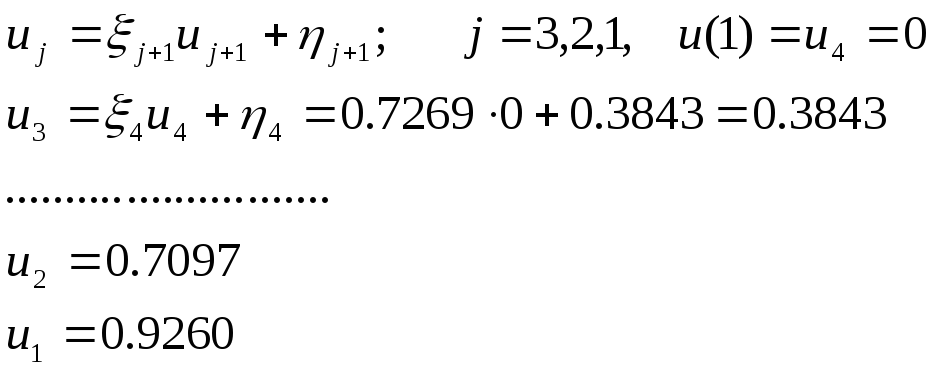
до N=4, тогда при ,

Ответ

x	0	1/4	1/2	3/4	1
u(x)	1	0.9260	0.7097	0.3843	0

Вычисления проведете сами по формулам

2. Основные понятия теории разностных схем: аппроксимация, устойчивость, сходимость.

Разностная схема это аппроксимирование некоторой дифференциальной задачи системой конечно- разностных уравнений.

Рассмотрим дифференциальную задачу с начальными и краевыми условиями в виде

B,L и так далее, более простыми отношениями, которые называются конечно разностными:

Здесь L_h, B_h-разностные операторы, u-решение разностных уравнений, функции f, ψ, θ – приближенные значения функций F, Ψ, Θ соответственно. Предположим, что известно точное решение диф задач(1)-(3), если поставить это решение в разностную схему (4), получится некоторое отклонение, которое называется невязкой и имеет вид:

---

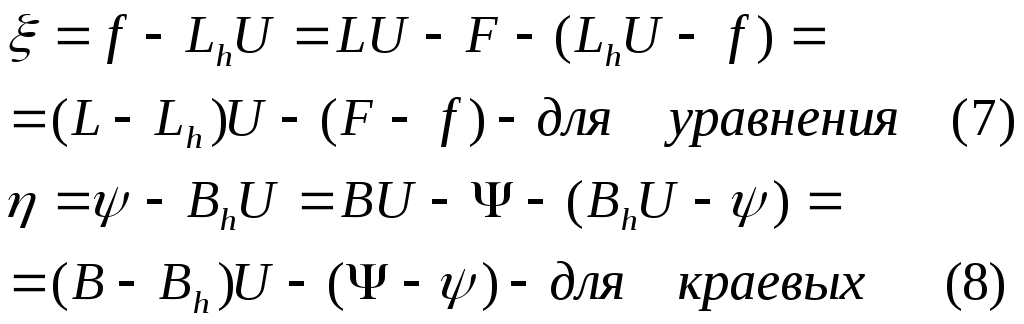
Аппроксимация - когда с уменьшением шагов невязка стремиться к нулю, то есть ее смысл состоит в том, что с уменьшением шагов конечноразностные уравнения стремятся к исходным. Обычно аппроксимация обозначается

Говорят, что разностная схема устойчива, если малые изменения исходных данных приводят к малым изменениям решения, то есть если

Говорят, что разностная схема сходится (к точному значению) если

Если погрешность решения :

Говорят, что разностная схема сходится кс к-ым порядком пот h и s-м порядком по τ.

Задача 2.1 . Используя метод конечных разностей составить решение краевой задачи с точностью , при h=0,1:

;

Решение:

Требуется найти значение искомой функции на [2; 2,3], h=0,1

задача ищется в виде:

Краевые условия примут вид

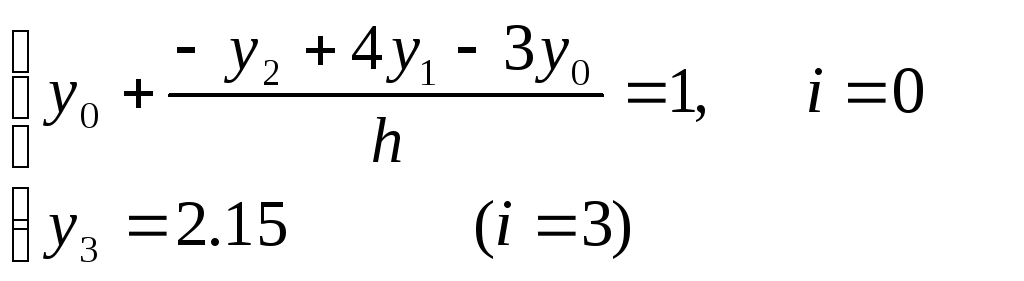
Таким образом задача сводится к решению системы лин уравнений

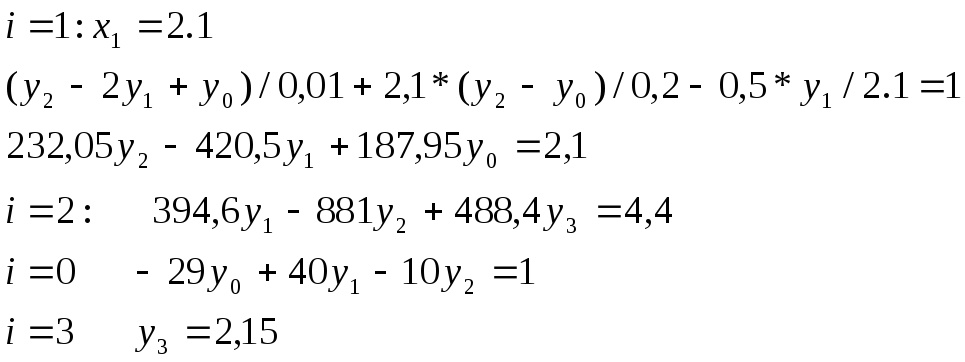
Неизвестные можно найти из системы

Таким образом получаем таблицу искомых значений

х	2	2,1	2,2	2,3
у	2,235	2,185	2,158	2,15

---

3.Разностная аппроксимация задачи Дирихле для уравнения Пуассона: постановка разностной задачи, оценка погрешности.

Уравнение элиптич типа имеет вид

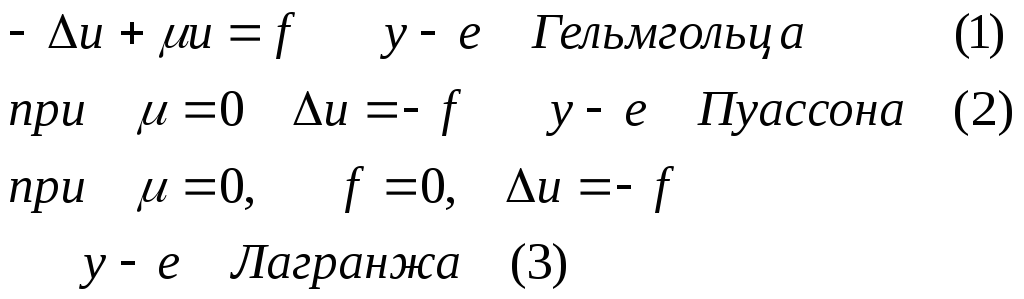
У-е Пуассона описывает распределение электрического потенциала в среде с плотностью заряда и электрической проницаемостью.

Рассмотрим так называемую задачу Дирихле или краевую задачу для уравнения Пуассона

Воспользуемся сеткой с узлами

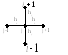
Если аппроксимировать 2- е производные в операторе

конечноразностными функциями на 5–ти точечном шаблоне «крест», то можно построить разностную схему

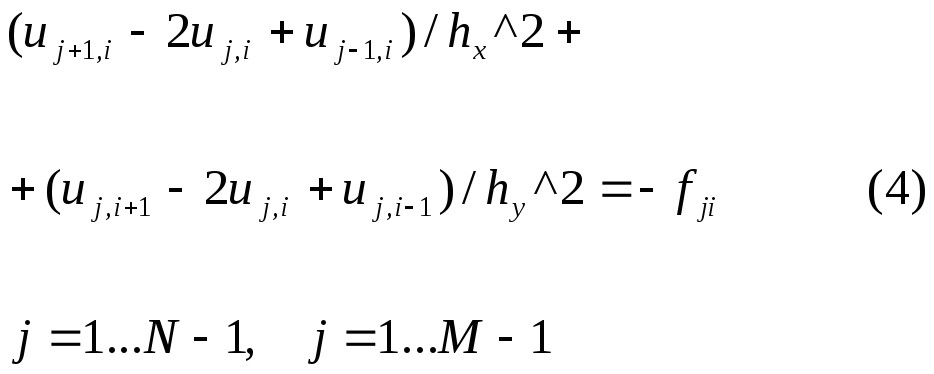
Схема (4) имеет погрешность аппроксимации , то есть эта схема второго порядка; значения

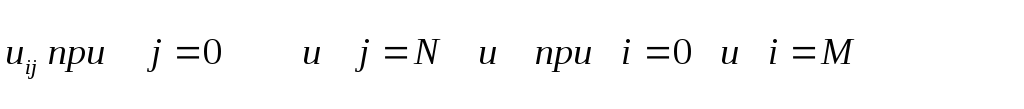
задаются краевыми условиями.

Задача 3.1.Используя метод сеток, составить приближенное решение задачи Дирихле для уравнения Лапласа в квадрате АВСD с вершинами А(0;0), В(0;1), С(1;1), D(1;0), взяв шаг h=0,5; Г – граница рассматриваемой области; .

Вычислим значения в граничных точках по заданной формуле

Е(0.5;1), F(1;0.5), G(0.5;0), H(0;0.5)

u(A)=u(0,0)=0

u(B)=u(0,1)=0+1=0

u(C)=u(1,1)=2

u(D)=u(1,0)=1

u(E)=u(0.5;1)=1.5;

u(F)=1.5

u(G)=0.5

u(H)=0.5

---

Смотрите также файлы

• Численные методы.doc

• Чегодаев.doc

• ЧАСТЬ 3 ГЛАВЫ 7.1-7-11.doc

• хакыкы курсовой.docx

• Философия.docx