ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.04.2024
Просмотров: 30
Скачиваний: 1
Для нахождения решения используем шаблон
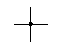
По формуле
найдем значение функции в точке I.
Решения запишем в виде таблицы
|
1 |
1.5 |
2 |
|
0.5 |
1 |
1.5 |
|
0 |
0.5 |
1 |
4. Двухслойные разностные схемы для уравнения теплопроводности: построение, исследование погрешности аппроксимации.
Рассмотрим уравнение теплопроводности,
которое дополняется начальными и краевыми условиями
В этих уравнениях u-температура, a^2-коэффициент теплопроводности, f(x,t)- описывает внутр-е источники тепла.
Для существования
и единственности решения уравнения (1)
не требуется согласования начальных и
краевых условий, то есть допускаются
разрывы функции u(x,0)
на границах в начальный момент времени
t=0.
Построим равномерную сетку, где
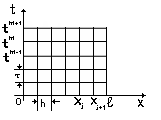
Значения сеточных
функций принято обозначать
.
Если выбрать четырехузловой шаблон
(смотрите рисунок, там где стрелочками
помеченно) то можно рассмотреть явную
разностную схему
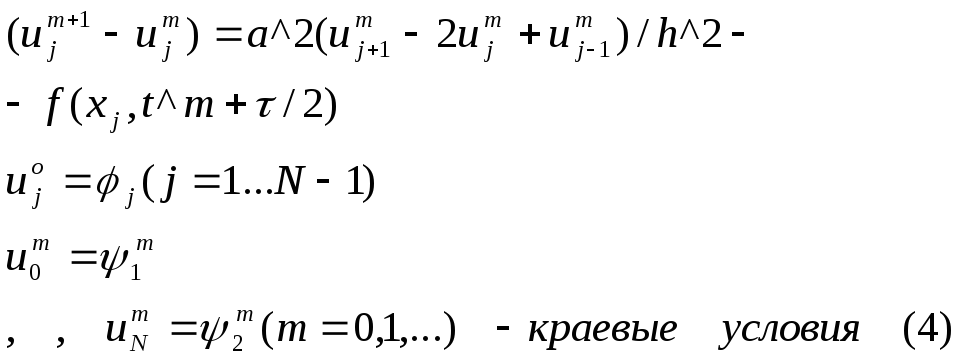Погрешность данной
аппроксимации равна
,
однако если при f=0
выбрать такое отношение шагов
,
что
=1/6,
то погрешности конечно-разностных
производных по x
и по t
взаимно компенсируется и порядок
аппроксимации возрастает до
.
Задача 4.1.
Используя метод сеток, составить решение
уравнения теплопроводности
при заданных начальных и краевых условиях
;
;
,
где
для
,
при h=0,2,
.
Решение:
-
начальное
условие
-
краевые условия
(так
как
, но по условию
)
(так как
=0
)
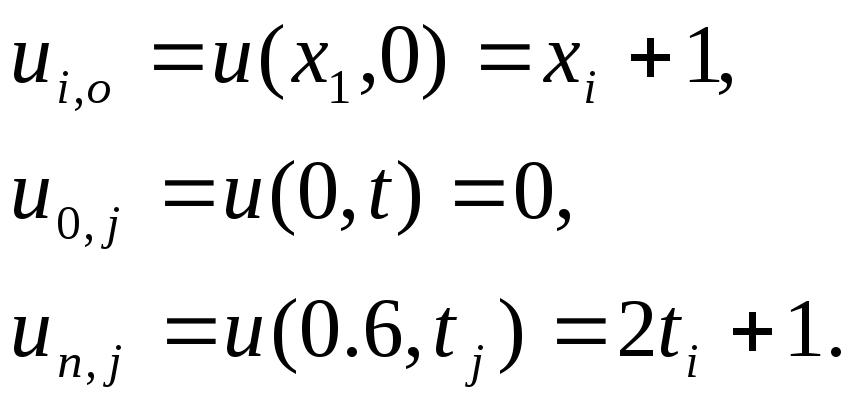
Для определения значения во внутренних точках, применим формулу
Все ручные расчеты будем оформлять в таблицу
|
|
i |
0 |
1 |
2 |
3 |
|
j |
|
0 |
0.2 |
0.4 |
0.6 |
|
0 1 |
0 0.01 |
0 0 |
1.2 0.95 |
1.4 1.25 |
1 1.02 |
5. Трехслойная разностная схема для уравнений гиперболического типа.
Рассмотри уравнение гиперболического типа, которое описывает распространение колебаний и волн (упругих, акустических и др) с её начальными и краевыми условиями.
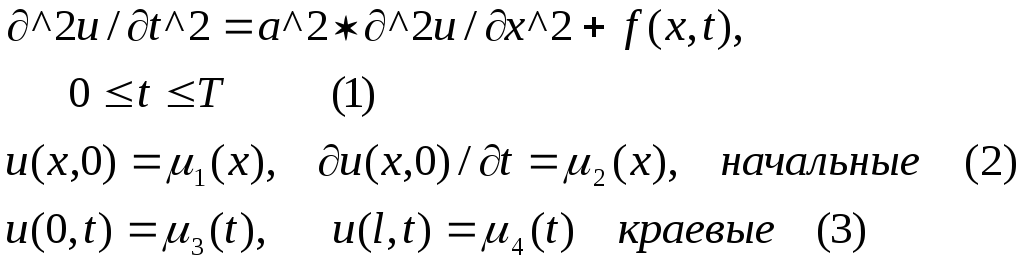
Для численного решения обычно используют простейшую трехслойную разностную схему, которая строится гна 5-ти узловом шаблоне
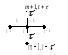
Тогда получается следующая трехслойная разностная схема
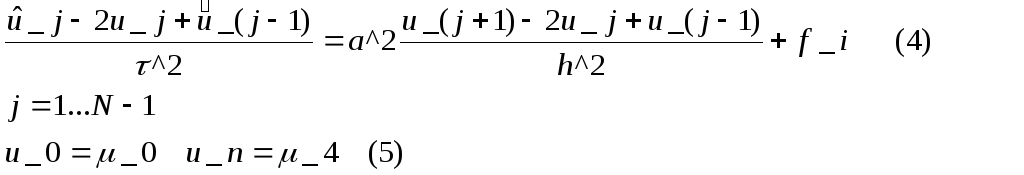
Для данной схемы
погрешность аппроксимирования
.
Чтобы начать вычисления по формуле (4), необходимо располагать значениями u0 и u1
---------------------------------------------------------------------------------------------------------------
Задача 5.1.
Используя метод сеток, составить решение
смешанной задачи для уравнения колебания
струны
с начальными условиями:
;
,
и краевыми условиями
;
,
взяв h=0,2
при
.
Решение: Суть метода заключается в том, что сначала находятся значения функции на конца, затем по ним соседние внутренние, по соседним соседние и так далее. На концах решения находятся по начальным условиям, у внутренние по специальным формула (они последние в решение)
количество
значений
количество
значений
Используя начальные
условия
,
и краевое
,
будем искать:
(значения
первой строки)
(значения
второго столбца)
(значения последнего
столбца таблицы)
Остальные значения внутренних точек ищем по формулам
(найдем значения,
которые записываются во вторую строчку,
где
)
где
даны по условию,
и
(по этой формул найдем значения третей
и четвертой строки)
все вычисления будем оформлять в виде таблице. (в ней подсчитаны значения лишь 1,2 и последн столбца и первой строки, остальное посчит сами )
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
0 0,2 0,4 0,6 |
0 0.04 0.16 0.36 |
0.04 |
0.16 |
0.36 |
0.64 |
0 0 0 0 |
