Файл: Численные методы.doc

1. Квадратурные формулы прямоугольников, трапеций и парабол (формула Симпсона).

- формулы прямоугольников: это простейшие квадратурные формулы, вытекающ из определения опред интеграла, как площади криволинейной трапеции. Разобьем наравных частей, получим,

, тогда

- формула левых прямоугольников

- формула правых прямоугольников

где предельная абсолютная погрешность определяется условием

- формула трапеции

где предельная абсолютная погрешность определяется условием

- формула парабол (формула Симсона). Обязательно должно быть четным.

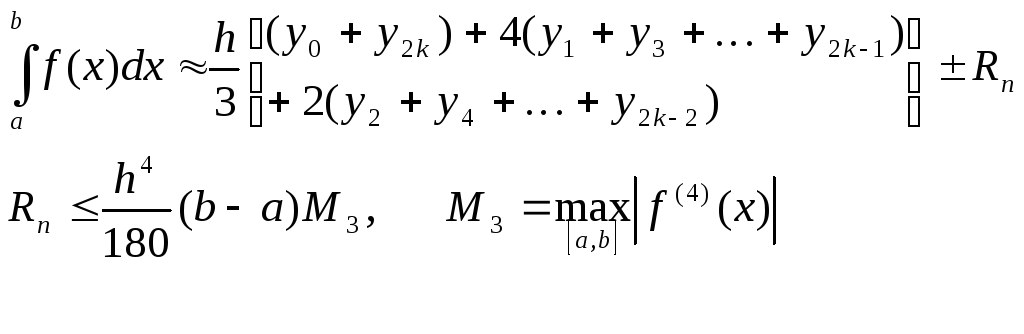
Задача 1.1. Вычислить по формуле Симпсона , принявn=8. Оценить погрешность по методу удвоения шага вычислений. Вычисления вести с пятью знаками после запятой. Сравнить со значением, найденным по формуле Ньютона - Лейбница.

Решение: рассчитаем шаг по формуле .

Рассмотрим подынтегральную функцию

По этим двум формулам подсчитаем значения

---

	4	4,5	5	5,5	6	6,5	7
	0,33333	0,32038	0,30902	0,29894	0,28990	0,28173	0,027123

* Таблица не влезла, вот её продолжение

	7,5	8
	0,26748	0,26120

*в конце некоторых дробей стоя нули, тем самым показываем что точность 5 знаков после запятой достигнута во всей таблице.

Общий вид формулы имеет вид

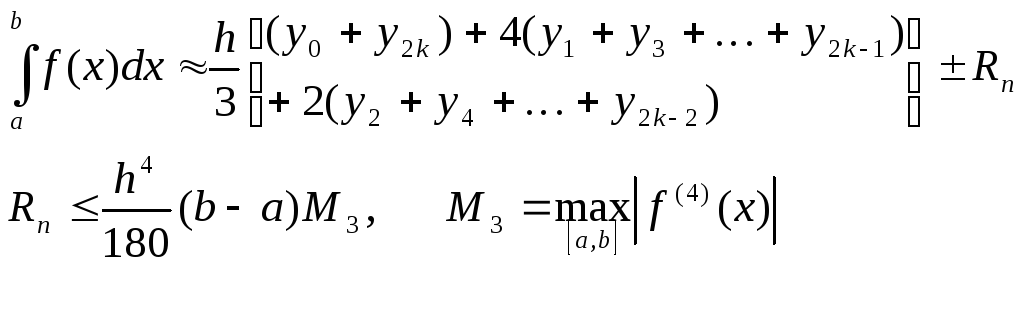
Найдем для п=8

Вычисли два интеграла, первый с шагом , обозначим его как, второй с шагом(из условия нахождения погрешности) и обозначим его

---

Вычислим погрешность

Следовательно искомый интеграл равен

Найдем интеграл по формуле Ньютона – Лейбница

Задача 1.2.Вычислить по формуле Симпсона , принявn=10. Оценить погрешность. Сравнить со значением, найденным по формуле Ньютона - Лейбница.

Решение :

Шаг вычислений

Подынтегральная функция

По этим формулам найдем значения для таблицы

	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
	1	0.90909	0.83333	0.76923	0.71429	0.66667	0.625	0.58824	0.55556	0.52632	0.5

В общем случае формулы нахождения:

Для случая получим формулы

---

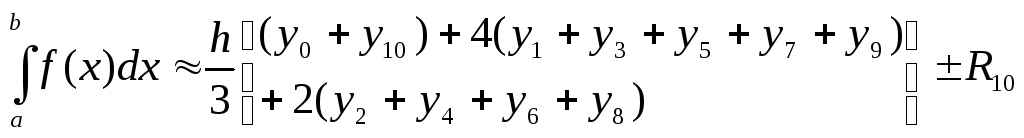
I – значение интеграла без учета погрешности

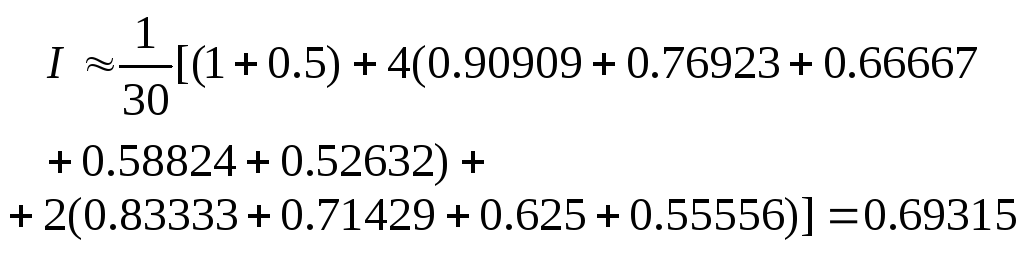
Точное значение находится по формуле Ньютона – Лейбница

Задача 1.3.Вычислить по формуле трапеций принявn=10 . Оценить погрешность. Сравнить со значением, найденным по формуле Ньютона – Лейбница

Решение:

Шаг вычислений

Подынтегральная функция

По этим формулам найдем значения для таблицы

	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
	1	1.0488	1.09545	1.14018	1.18322	1.22474	1.26491	1.30384	1.34164	1.3784	1.41421

В общем случае формулы нахождения:

---

Для случая получим формулы

I – значение интеграла без учета погрешности

е

Точное значение находится по формуле Ньютона – Лейбница

2. Методы Ньютона (касательных) и секущих (хорд) для решения нелинейных уравнений.

Метод секущих

Пусть требуется вычислить действительный корень уравнения, изолированный на отрезке(отделение корня произвольно, любым способом). Рассмотрим график функции, он будет иметь следующий вид, тогда. Соединим точки графикахордой. Уравнение прямой (хорды), проходящей через точкиимеет вид. За приближенное значение искомого корня примем абсциссуточки пересечения хорды АВ, проходящей через точкиимеет вид:

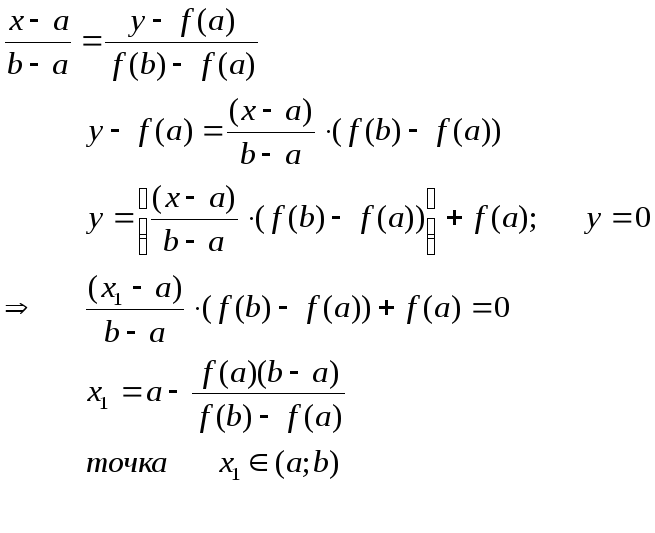
Если , то искомый корень найден,ес ли значении отлично от 0, то метод хорд применяют дальше. Если, то за новый, более узкий отрезок принимаюти соединяют хордой точки

. Точкой пересечения хорды с Ох (её асциссой) будет значение значение , которые вычисляются по формуле

---