ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.09.2024
Просмотров: 83
Скачиваний: 0
СОДЕРЖАНИЕ
Равноускоренное прямолинейное движение
3. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.
4. Инерция. Инерциальные системы отсчета. 1-й закон Ньютона.
5. Взаимодействие тел. Сила. Принцип суперпозиции сил. Проявления взаимодействия тел. Сила
6. Законы динамики Ньютона. Второй закон Ньютона
Третий закон Ньютона. Обратная задача динамики
7. Сила упругости. Виды деформаций. Закон Гука.
8. Сила трения: скольжения, качения, покоя. Коэффициент трения.
9. Закон всемирного тяготения. Гравитационное поле. Невесомость
10. Импульс тела. Закон сохранения импульса. Реактивное движение.
11. Механическая энергия и ее виды. Закон сохранения энергии.
12. Механическая работа и мощность. Кпд.
13.Колебательное движение и его характеристики. Виды колебаний.
Колебательное движение и его характеристики
14. Свободные и вынужденные колебания. Резонанс и его учет в технике.
15. Механические волны. Виды волн. Длина волны.
Скорость распространения волны
16. Звуковые волны. Ультразвук и его использование в технике и медицине.
10. Импульс тела. Закон сохранения импульса. Реактивное движение.
Импульс
тела(материальной точки)![]() –
векторная физическая величина, равная
произведению массы этого тела (материальной
точки) на его скорость:
–
векторная физическая величина, равная
произведению массы этого тела (материальной
точки) на его скорость:
![]()
Единицей импульса в СИ является 1 кг·м/с.
Изменение
импульсаматериальной точки![]() за
некоторый промежуток времени – вектор,
равный разности конечного и начального
вектора импульса:
за
некоторый промежуток времени – вектор,
равный разности конечного и начального
вектора импульса:![]() (рис.
1).
(рис.
1).
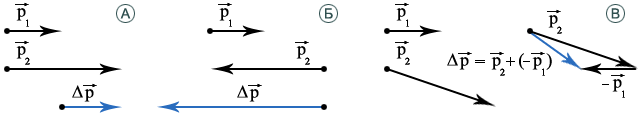
Рис. 1
Импульс
силы– это векторная физическая
величина, равная произведению среднего
значения силы на промежуток времени ее
действия:![]() .
.
Второй закон Ньютона для материальной точки может быть записан с использованием понятий импульса силы и импульса материальной точки (в импульсном виде):
![]() ,
,
следовательно,
![]()
При скоростях близких к скорости света следует пользоваться другим определением импульса материальной точки.
Импульсом системы телназывается сумма векторов импульсов всех тел этой системы.
Силы, действующие между телами системы, называются внутренними.Силы, характеризующие воздействие тел, не входящих в систему, на тела системы, называютсявнешними.
На основе второго и третьего законов Ньютона может быть доказан закон сохранения импульса системы тел: в инерциальной системе отсчета импульс системы тел остается неизменным, если на систему не действуют внешние силы.
Приближенно он выполняется и в случаях, когда внешние силы конечны, а процессы, происходящие в системе, являются быстрыми и вызваны большими внутренними силами (столкновение тел, взрыв, выстрел и т. п.). Кроме того, если сумма внешних сил не равна нулю, но проекция суммы внешних сил на выбранную ось равна нулю, то сохраняется проекция импульса системы на эту ось.
На рисунке 2 приведены примеры реальных процессов, в которых закон сохранения импульса системы тел выполняется точно, приближенно и в проекции на выбранную ось.
|
|
|
|
|
|
|
|
Рис. 2
Следует иметь в виду, что импульс тела – векторная физическая величина и его сохранение в случае равенства нулю суммы внешних сил означает выполнение векторного равенства. Например, при взаимодействии двух тел, движущихся в одной плоскости, это означает выполнение двух скалярных уравнений для проекций импульсов одновременно. Примером может служить нецентральный удар бильярдных шаров:
m1![]() 1x
+ m2
1x
+ m2![]() 2x
= m1u1x
+ m2u2x
2x
= m1u1x
+ m2u2x
m1![]() 1y
+ m2
1y
+ m2![]() 2y
= m1u1y
+ m2u2y
2y
= m1u1y
+ m2u2y
Реактивное движение– движение тела, возникающее при отделении от него с какой-либо скоростью некоторой его части. Если отделение частей тела происходит быстро, то для этих частей (осколки снаряда, ракета (рис. 3) и вылетающая порция продуктов сгорания топлива, тело медузы и порция выброшенной воды) выполняется закон сохранения импульса.
|
|
11. Механическая энергия и ее виды. Закон сохранения энергии.
Кинетическая энергия– скалярная физическая величина, характеризующая движущееся тело и равная для материальной точки половине произведения ее массы на квадрат ее скорости:
![]()
Единицей кинетической энергии в СИ является джоуль (Дж).
При скоростях, близких к скорости света, следует пользоваться иным определением кинетической энергии.
Кинетическая энергия протяженного тела равна сумме кинетических энергий его малых частей, которые можно считать материальными точками.
Используя второй закон Ньютона, можно доказать теорему об изменении кинетической энергии тела: в инерциальной системе отсчета изменение кинетической энергии тела равно работе всех сил, как внутренних, так и внешних, действующих на это тело.
Если
на прямолинейном участке траектории
на тело, совершающее перемещение x,
действуют две постоянные силы![]() и
и![]() ,
направленные под углами1
и 2
к перемещению, то изменение кинетической
энергии тела равно:
,
направленные под углами1
и 2
к перемещению, то изменение кинетической
энергии тела равно:
12. Механическая работа и мощность. Кпд.
Механическая
работаAпостоянной силы![]() на
перемещение
на
перемещение![]() –
это скалярная физическая величина,
равная произведению модуля силыF,
модуля перемещенияsи косинуса угла
между направлениями силы и перемещения.
–
это скалярная физическая величина,
равная произведению модуля силыF,
модуля перемещенияsи косинуса угла
между направлениями силы и перемещения.
А = Fs cos =Fxs,
где Fx– проекция силы на направление перемещения (рис. 4).
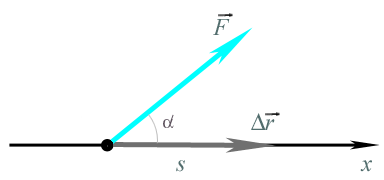
Рис. 4
Работа
постоянной силы в зависимости от угла
между векторами силы
![]() и
перемещения
и
перемещения![]() может
быть положительной, отрицательной и
равной нулю (рис. 5).
может
быть положительной, отрицательной и
равной нулю (рис. 5).
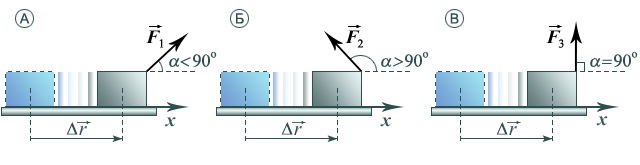
Рис. 5
Единицей работы в СИ является джоуль (Дж).
В общем случае действия переменной силы на криволинейном участке траектории расчет работы оказывается более сложным.
Мощность– скалярная физическая величина, равная отношению работы силыAк промежутку времениt, в течение которого она была произведена:
![]()
Мощность силы может измеряться во времени N(t)
Единицей мощности в СИ является ватт (Вт).
При
воздействии силы
![]() на
тело, движущееся со скоростью
на
тело, движущееся со скоростью![]() (рис.
7), мощность этой силы равна:
(рис.
7), мощность этой силы равна:
N
= F![]() cos .
cos .
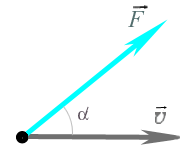
Рис. 7
Часто термины работаи мощность относят к устройству, благодаря которому возникают силы, совершающие работу. Говорят о работе человека, мощности электродвигателя или двигателя автомобиля вместо работы и мощности силы натяжения веревки, с которой человек тянет сани, или работы и мощности внутренних сил или мощности сил сопротивления воздуха при движении автомобиля. В простейших случаях (подъемный кран поднимает груз) это вполне допустимо, однако в ряде случаев требует более аккуратного рассмотрения. Так, в случае движения автомобиля силой тяги является сила трения шин об асфальт, а ее работа равна нулю. В случае вертолета, зависшего над землей, сила тяги равна силе тяжести, мощность силы тяги равна нулю, однако энергия сгорающего топлива затрачивается на сообщение кинетической энергии потокам воздуха, отбрасываемого вниз.
При использовании простейших механизмов человек стремится совершить действия, которые не под силу выполнить «голыми руками» (поднять груз, сдвинуть тело и т.д.). Такие механизмы характеризуются физической величиной, называемой коэффициентом полезного действия(КПД). В механике обычно под КПД механизма понимают отношение полезной работы к затраченной.
![]()
Когда
говорят о затраченной работе, то имеют
в виду работу силы
![]() ,
которой человек воздействует на механизм.
Если речь идет о полезной работе, то
имеют в виду работу силы
,
которой человек воздействует на механизм.
Если речь идет о полезной работе, то
имеют в виду работу силы![]() ,
приложенной к телу при его равномерном
перемещении. Так, если человек поднимает
груз с помощью системы блоков, перемещая
конец веревки на длинуs1,
а груз при этом перемещается (поднимается)
на высоту s2
под действием силы F2
= mg,
то КПД механизма, обозначаемый буквой
,
будет равен:
,
приложенной к телу при его равномерном
перемещении. Так, если человек поднимает
груз с помощью системы блоков, перемещая
конец веревки на длинуs1,
а груз при этом перемещается (поднимается)
на высоту s2
под действием силы F2
= mg,
то КПД механизма, обозначаемый буквой
,
будет равен: