Файл: Bil-mekhan.doc

13.Колебательное движение и его характеристики. Виды колебаний.

Математический и пружинный маятники.

Колебательное движение и его характеристики

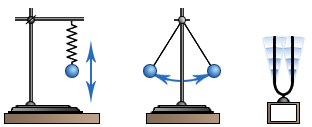
Рис. 1

Механические колебания– это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве. Различают периодические и непериодические колебания.Периодическиминазывают колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени.

Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него (рис. 1). В физике рассматривают и другие колебания – процессы, обладающие той или иной степенью повторяемости во времени (например, электромагнитные колебания.)

Колебания можно классифицировать по условиям возникновения (свободные, вынужденные, автоколебания) и по характеру изменения во времени кинематических характеристик (пилообразные, гармонические, затухающие).

Если колебания совершаются в системе за счет первоначально сообщенной энергии, то они называются свободными. Примером таких систем являются модели колеблющихся тел:математическиймаятник ипружинный.

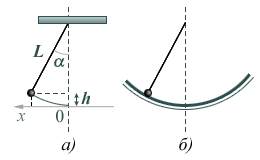
Математический маятник – колеблющаяся материальная точка, подвешенная на невесомой и нерастяжимой нити. К этой модели ближе всего массивное тело (шар), размер (диаметр) которого много меньше длины нити. Если его отклонить от положения равновесия, увеличив при этом потенциальную энергию системы «шар–нить», то будут наблюдаться колебательные движения этой системы. Колебательное движение системы «шар–нить» будет наблюдаться и в том случае, если шару сообщить кинетическую энергию, т.е. заставить его двигаться.

Рассмотрев малые колебания математического маятника (рис. 4), при которых отклонение его от положения равновесия х(t) <<L, можно получить выражение для периода его колебаний. Как мы знаем, в любой момент времени для этой системы выполняется закон сохранения механической энергии:

Выразив высоту hчерез координатуxпо оси 0Х(рис. 4,а) и учитывая, что при малых значенияххугол между нитью и вертикалью тоже мал, используем что для такого угла отклонения соотношение sintg.

Поэтому можно утверждать что малые колебания математического маятника происходят по гармоническому закону

x = A sin (t + ₀),

где

,

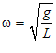т.е. с периодом

По гармоническому закону y=Asin (t+ĵ₀) колеблется и пружинный маятник, состоящий из груза массойmи пружины жесткостьюk(рис. 5).

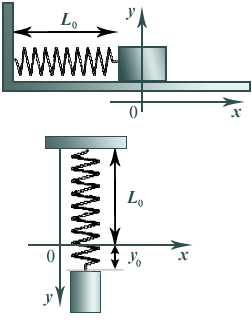
Рис. 5

При этом период его колебания равен

Если горизонтальный пружинный маятник колеблется относительно положения равновесия, где пружина не растянута, то вертикальный пружинный маятник колеблется относительно положения равновесия, где ky₀=mg.

Период и частота свободных гармонических колебаний в обоих случаях определяются только собственными параметрами системы: длиной нити математического маятника или жесткостью пружины и массой груза пружинного маятника, поэтому свободные колебания часто называют собственными колебаниями, а частоту, с которой они происходят,собственной частотой колебанийсистемы.

14. Свободные и вынужденные колебания. Резонанс и его учет в технике.

Если колебания совершаются в системе за счет первоначально сообщенной энергии, то они называются свободными. Примером таких систем являются модели колеблющихся тел:математическиймаятник ипружинный.

Вынужденные колебания– колебания, происходящие под действием меняющейся во времени внешней силы, которая совершает работу. За счет этого энергия колебательной системы увеличивается. Такой процесс можно описывать как процесс притока энергии в систему извне в ходе самих колебаний. Примером систем, в которых происходят вынужденные колебания, являются качели, раскачиваемые человеком, груз, висящий на пружине, точку подвеса которой периодически поднимают и опускают.

Если внешняя сила, действующая на систему, изменяется с течением времени по закону косинуса или синуса, то возникающие в системе вынужденные колебания будут гармоническими. При этом частота вынужденных колебаний будет совпадать с частотой изменения внешней силы.

Если при вынужденных колебаниях энергия, поступающая непрерывно или периодически от внешнего источника, восполняет потери, возникающие за счет работы силы трения, то колебания оказываются незатухающими.

Амплитуда вынужденных колебаний определяется амплитудой колебаний внешней силы, а также соотношением между частотой изменения этой силы и собственной частотой колебательной системы.

При вынужденных колебаниях может наблюдаться явление резкого возрастания амплитуды Aвынужденных колебаний системы –резонанс. Это явление возникает тогда, когда частота вынуждающей силы приближается к собственной частоте колебаний этой системы. При этом энергия, поступающая в колебательную систему, также равна потерям энергии за счет работы силы трения, однако баланс энергий наступает при другой амплитуде колебаний.

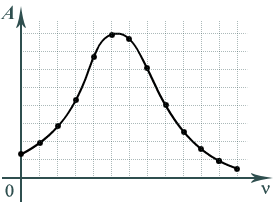
Рис. 7

Резонанс может возникать и тогда, когда частота колебаний вынуждающей силы кратна собственной частоте колебаний системы.

Зависимость амплитуды колебаний системы от частоты вынуждающей силы (рис. 7) называется резонансной кривой.

В технике используются устройства, в которых незатухающие колебания поддерживаются за счет энергии источника, автоматически включаемого и выключаемого самой колебательной системой. Момент, когда требуется подать энергию в колеблющуюся систему, отслеживает система обратной связи, которая открывает и закрывает клапан поступления энергии. Такие системы с регулированием поступления энергии за счет обратной связи называются автоколебательными, а сами колебания в таких системах – автоколебаниями.Примером такой системы могут служить маятниковые часы, где источником энергии является гиря на цепочке, роль обратной связи и «клапана» выполняет анкерный механизм, а автоколебания совершает маятник, который имеет собственную частоту колебаний, равную 1с

15. Механические волны. Виды волн. Длина волны.

В среде между ее частицами существуют силы взаимодействия. Если за счет внешнего источника энергии (внешней силы) вызвать колебания одних частиц среды, то возникают вынужденные колебания соседних частиц, которые, в свою очередь, вызывают колебания следующих частиц среды. Процесс распространения колебанийчастиц среды или другого типа возмущения среды называютмеханической волной.

Волны, в которых колебания частиц происходят вдоль направления распространения волны, называются продольными.

Волны, в которых колебания частиц происходят перпендикулярно направлению распространения волны, называются поперечными.

В продольной волне возмущения представляют собой сжатие (или разрежение) среды, а в поперечной – смещение (сдвиг) одних слоев среды относительно других. Пример продольных волн – распространение звука (зон сжатия) в газах, жидкостях и твердых телах, пример поперечных волн – распространение звука в твердом теле, волны на поверхности воды, на веревке или на пружине.

Деформация сжатия всегда сопровождается возникновением силы упругости, в то время как деформация сдвига приводит к появлению сил упругости только в твердых телах; сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому продольные волны могут распространяться во всех средах: жидких, твердых, газообразных, а поперечные – только в твердых.

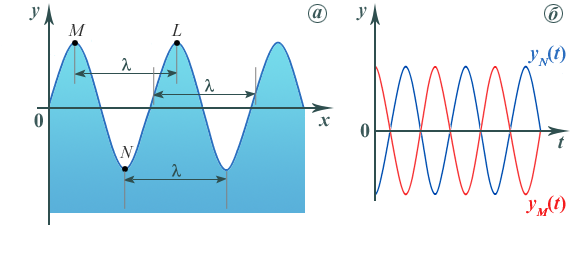
Рис. 2

График зависимости смещения каждой частицы среды от времени представляет собой синусоиду, сдвинутую относительно синусоиды для частицы в другой точке в соответствии со сдвигом фаз (рис. 2,б) Минимальное расстояние между точками волны, колеблющимися в фазе, т.е. с разностью фаз, равной 2, называютдлиной волны.

Геометрическое место положений точек волны в момент времени tтакже представляет собой синусоиду (см. рис. 2,а) вида

y(x) = A sin (kx).

где

 = 2/T, k = 2/

Аналогичные соотношения можно записать и для продольной волны, только в ней y(t,x) будет смещением частиц среды относительно положения равновесия вдоль осиx, по которой распространяется волна.