Файл: Bil-mekhan.doc

Для поиска искомых сил может помочь и третий закон Ньютона, так как, решив задачу с одним телом и рассчитав силы, действующие на него, можно сделать вывод и о другой силе, входящей в третий закон Ньютона. Так, определив силу, действующую на человека, качающегося на качелях, в нижней точке траектории, можно по третьему закону Ньютона сделать вывод о силе, с которой человек давит на качели в этой точке, т.е. о весе человека при таком движении. Рассмотрение равномерного движения самолета с летчиком по окружности, расположенной в вертикальной плоскости, с помощью второго и третьего законов Ньютона приводит к выводу, что вес летчика наибольший в нижней точке траектории

7. Сила упругости. Виды деформаций. Закон Гука.

Силой упругостиназывается сила, характеризующая действие, которое оказывает деформированное тело (нить, пружина, трос и др.) на соприкасающееся с ним другое тело.

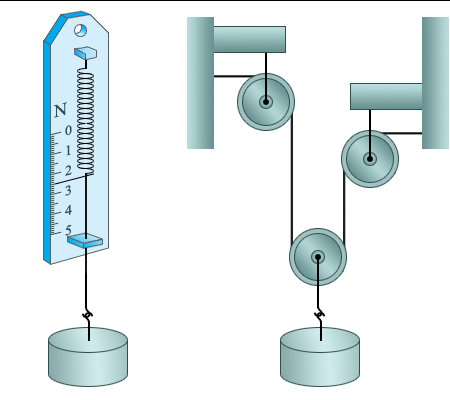
Рис. 7

Для пружин и стержней при малых деформациях установлено, что сила упругости пропорциональна изменению длины lпружины или стержня, т.е. пропорциональна деформации:

F_упр=kl.

Это соотношение называют законом Гука, а коэффициент пропорциональности k–жесткостьюили упругостью тела (стержня, пружины). Чем больше жесткость тела, тем меньше оно деформируется при заданной силе. Величинаkопределяется геометрическими размерами тела и материалом, из которого оно изготовлено. Если форма тела (стержня, пружины или резинового жгута) начинает существенно меняться, то пропорциональность междуF_уприlнарушается (рис. 8).

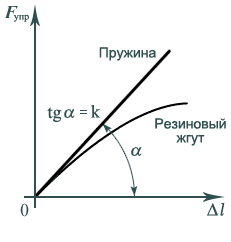
Рис. 8

Нить – модель тела с нулевой массой и с выделенной осью, которое способно изгибаться под бесконечно малой нагрузкой. Поэтому ее можно перебросить через блок, и сила натяжения будет везде одинакова.

Пружина – модель тела (обычно с нулевой массой), которое действует на рассматриваемое тело не только в растянутом, но и в сжатом состоянии. Причем закон Гука выполняется для пружины не только при растяжении, но и при сжатии.

Силой натяжения нити или пружины называют иногда силу воздействия одних частей нити (пружины) на другие, соседние части. Сила натяжения нити (пружины) направлена вдоль нити (оси пружины) и для невесомой нити (пружины) одинакова по всей длине нити (пружины).

Прямая пропорциональность между удлинением пружины и приложенной силой используется в простейшем приборе для измерения силы – динамометре.

8. Сила трения: скольжения, качения, покоя. Коэффициент трения.

При соприкосновении тел между ними наблюдается взаимодействие. Силу, характеризующую это взаимодействие, называют силой реакции поверхности, обозначают как и представляют в виде суммы сил, составляющих ее:, где–сила нормальной реакции поверхности, направленная перпендикулярно этой поверхности,–сила трения, направленная вдоль этой поверхности.

При контакте гладких поверхностей F_тр= 0 и.

Простейшее соотношение между модулями сил, составляющих силу реакции поверхности, формулируется в виде закона сухого трения:

1. При скольжении модуль  силы трения прямопропорционален модулю силы нормальной реакции:

Коэффициент пропорциональности –коэффициент трения скольженияне зависит ни от площади соприкасающихся поверхностей, ни от скорости их относительного движения.

2. Если скольжение не происходит, то максимально возможное значение силы трения покоя равно значению силы трения скольжения:

Значение и направление силы трения покоя отыскиваются из услови неподвижности тела относительно опоры.

При постепенном увеличении (со временем) силы , приложенной вдоль трущихся поверхностей, происходит аналогичный рост силы трения покоя (рис. 9). Силы, действующие вдоль поверхности, скомпенсированы, поэтому тело покоится. Когда модуль силыдостигнет значенияN, модуль силы трения покоя достигает своего максимального значения, а затем сила трения уже не уравновешивает внешнюю силу, и тело начинает скользить, разгоняясь (рис. 9).

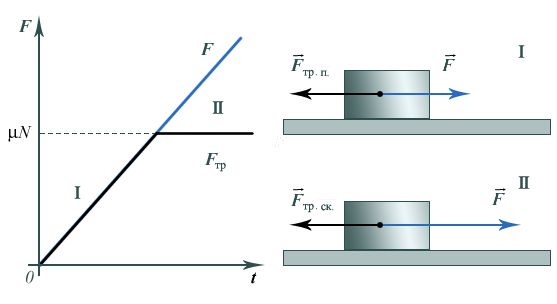
Рис. 9

В реальных экспериментах закон сухого трения выполняется приближенно.

9. Закон всемирного тяготения. Гравитационное поле. Невесомость

Закон всемирного тяготения – сила гравитационного притяжения любых двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.

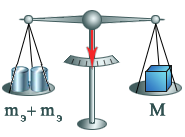
Гравитационную массу m₁(илиm₂) определяют сравнением ее с массой эталонного тела – цилиндра из платино-иридиевого сплава, масса которого принята за 1 кг (рис. 3). Процесс сравнения масс на рычажных весах называется взвешиванием (рис. 4). Гравитационная постояннаяG= 6,67·10^–11Н.м²/кг²впервые была измерена английским физиком Кавендишем в 1798 году.

Закон всемирного тяготения сформулирован для материальных точек. Если его применять к протяженному телу, то это тело следует разбить на малые части, а затем использовать принцип суперпозиции сил.

Ньютон доказал, что закон можно применять для расчета сил взаимодействия между симметричными сферическими телами, если считать, что r– это расстояние между их центрами (рис. 5).

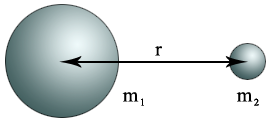
Рис. 5

Для расчета силы притяжения между двумя телами произвольной формы (например, два куба) закон всемирного тяготения в таком виде неприменим.

Силу всемирного тяготения называют силой тяжести, если рассматривают притяжение к Земле тел, которые достаточно малы по сравнению с размером самой Земли.

Для тел массой m, расположенных близко к поверхности Земли, установлено, что сила притяжения примерно равна:

где g9,8 м/с²– ускорение свободного падения. При точном измеренииgдолжно зависеть от распределения пород на Земле, места расположения тела на Земле и от высоты над уровнем моря.

На полюсах Земли ускорение свободного падения больше, так как Земля сплюснута с полюсов.

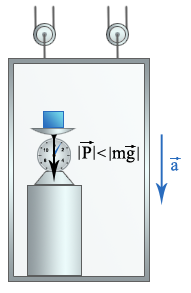
Рис. 6

Вес тела– это сила, с которой тело вследствие притяжения Земли давит на горизонтальную опору или растягивает вертикальный подвес. Таким образом, если на чаше весов стоит гиря, то вес – это сила, действующая не на гирю, а на чашу весов (рис. 6). Вес тела действует на подставку (опору) или подвес. При взвешивании в системе отсчета, покоящейся относительно Земли, вес неподвижного тела и сила тяжести совпадают, если не учитывать малые поправки, связанные с вращением Земли. Если весы движутся с ускорением, то вес может быть и больше, и меньше силы тяжести. Так, точные пружинные весы показывают вес тела, а не силу притяжения к Земле. На экваторе или в лифте, движущемся с ускорением, направленным вниз, вес тела меньше силы тяжести.

Если тело не давит на опору или не натягивает подвес, то говорят, что тело находится в состоянии невесомости. Если лифт и весы падают с ускорением свободного падения независимо друг от друга, то груз не давит на чашу, поэтому вес груза равен нулю, т.е. груз находится в состоянии невесомости.