ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.09.2024
Просмотров: 79
Скачиваний: 0
СОДЕРЖАНИЕ
Равноускоренное прямолинейное движение
3. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.
4. Инерция. Инерциальные системы отсчета. 1-й закон Ньютона.
5. Взаимодействие тел. Сила. Принцип суперпозиции сил. Проявления взаимодействия тел. Сила
6. Законы динамики Ньютона. Второй закон Ньютона
Третий закон Ньютона. Обратная задача динамики
7. Сила упругости. Виды деформаций. Закон Гука.
8. Сила трения: скольжения, качения, покоя. Коэффициент трения.
9. Закон всемирного тяготения. Гравитационное поле. Невесомость
10. Импульс тела. Закон сохранения импульса. Реактивное движение.
11. Механическая энергия и ее виды. Закон сохранения энергии.
12. Механическая работа и мощность. Кпд.
13.Колебательное движение и его характеристики. Виды колебаний.
Колебательное движение и его характеристики
14. Свободные и вынужденные колебания. Резонанс и его учет в технике.
15. Механические волны. Виды волн. Длина волны.
Скорость распространения волны
16. Звуковые волны. Ультразвук и его использование в технике и медицине.
Механика
Механическое движение. Относительность движения. Система отсчета. Модели тел и основные понятия.
Движение– это изменение положения тела или его частей в пространстве относительно другого тела, выбранного за тело отсчета, с течением времени.
Система отсчета– это совокупность тела отсчета, связанной с ним системы координат и часов.
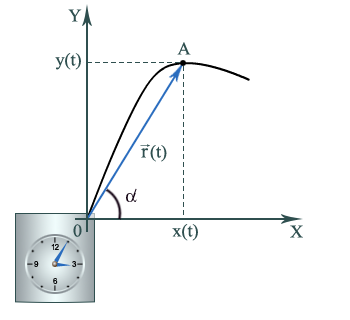
Материальная точка– идеализированная модель, соответствующая физическому телу, размерами которого в данных условиях можно пренебречь. На практике тело можно принять за материальную точку тогда, когда оно движется поступательно (не изменяя ориентацию относительно тела отсчета), или если его размеры оказываются намного меньше расстояний, рассматриваемых в данном движении.
Твердое тело – тело, деформациями которого при движении можно пренебречь.
Траектория– непрерывная линия, образованная множеством точек, через которые проходит движущаяся материальная точка в данной системе отсчета. Поэтому в разных системах отсчета траектория одного и того же движения имеет разную форму.
Понятие траектории используют лишь в классической механике для макромира. В микромире, где движение описывается квантовой механикой, понятие траектории теряет смысл.
Путьs– это скалярная физическая величина, длина участка траектории, пройденного материальной точкой за данный промежуток времени. Единица в СИ – метр (м).
2. Характеристики механического движения: перемещение, скорость, ускорение. Виды движения (равномерное, равноускоренное ) и их графическое описание.
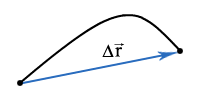
Перемещение![]() (или
(или![]() )
– вектор, соединяющий положения
движущейся материальной точки в начале
и в конце некоторого промежутка времени.
При криволинейной траектории модуль
вектора перемещения не совпадает с
длиной пройденного пути, т.е. с длиной
кривой линии.
)
– вектор, соединяющий положения
движущейся материальной точки в начале
и в конце некоторого промежутка времени.
При криволинейной траектории модуль
вектора перемещения не совпадает с
длиной пройденного пути, т.е. с длиной
кривой линии.
Скорость
![]() –векторная физическая величина,
характеризующая быстроту изменения
положения тела и равная пределу, к
которому стремится отношение
–векторная физическая величина,
характеризующая быстроту изменения
положения тела и равная пределу, к
которому стремится отношение![]() ,
т.е отношение перемещения
,
т.е отношение перемещения![]() к
промежутку времениt,
за которое произошло это перемещение,
если промежуток времени уменьшается
до нуля:
к
промежутку времениt,
за которое произошло это перемещение,
если промежуток времени уменьшается
до нуля:
![]()
Единица в СИ – метр в секунду (м/с).
Если
тело движется по прямой, то вдоль этой
прямой выбирают направление одной из
осей системы координат, например оси
0X, относительно которой рассматривается
движение. Если перемещение тела происходит
по направлению оси, то проекция вектора
скорости![]() xположительна, если против оси, то эта
проекция отрицательна.
xположительна, если против оси, то эта
проекция отрицательна.
Ускорение![]() –
векторная физическая величина,
характеризующая быстроту изменения
скорости и равная пределу, к которому
стремится отношение
–
векторная физическая величина,
характеризующая быстроту изменения
скорости и равная пределу, к которому
стремится отношение![]() ,
т.е. отношение изменения скорости
,
т.е. отношение изменения скорости![]() к промежутку времениt,
за который произошло это изменение, при
уменьшении промежутка времени до нуля:
к промежутку времениt,
за который произошло это изменение, при
уменьшении промежутка времени до нуля:
![]()
Единица в СИ – метр на секунду в квадрате (м/с2).
Если
материальная точка движется по прямой
линии, то вектор ускорения направлен в
ту же сторону, что и вектор скорости,
когда
![]() xувеличивается, и в противоположную
сторону, когда
xувеличивается, и в противоположную
сторону, когда![]() xуменьшается (рис. 3).
xуменьшается (рис. 3).
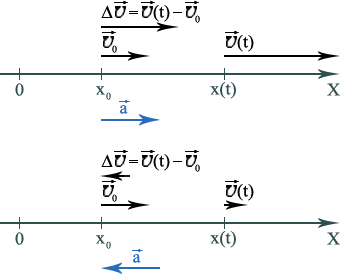
Рис. 3
Если направление оси координат 0Xсовпадает с направлением начального вектора скорости, то на первом рисунке проекция ускоренияaxположительна, а на втором отрицательна.
Это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. При равномерном прямолинейном движении скорость тела постоянна, а ускорение равно нулю.
Это самая простая модель движения, редко встречающаяся в реальности. При таком движении скорость тела постоянна, а координата может быть рассчитана по закону движения
![]() ,
,
где
x0–
начальная координата материальной
точки, а![]() 0x– проекция ее начальной скорости на
ось 0X.
0x– проекция ее начальной скорости на
ось 0X.
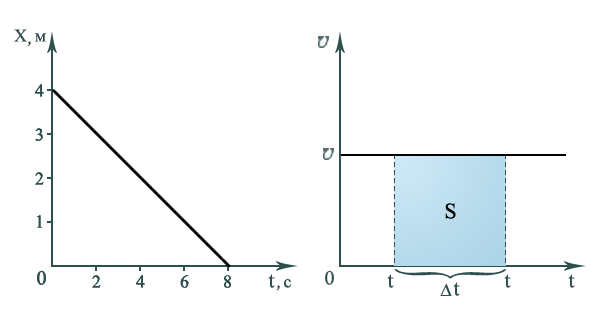
Графиком
такой зависимости в координатах (x,t) (рис. 4,а) является прямая
линия, тангенс угла наклона которой
задается проекцией скорости![]() 0x.
0x.
|
|
Равноускоренное прямолинейное движение
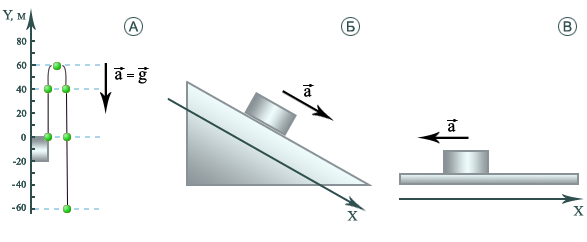
Рис. 5
Это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т.е. ускорение постоянно.
Примерами такого движения является свободное падение тел вблизи поверхности Земли и движение под действием постоянной силы.
При равноускоренном прямолинейном движении координата тела меняется с течением времени в соответствии с законом движения:
![]()
где
x0–
начальная координата материальной
точки,![]() 0x– проекция начальной скорости иax– проекция ускорения точки на ось 0X.
0x– проекция начальной скорости иax– проекция ускорения точки на ось 0X.
Проекция скорости материальной точки на ось 0Xв этом случае меняется по следующему закону:
![]()
При этом проекции скорости и ускорения могут принимать различные значения, в том числе и отрицательные.
Графики
зависимости
![]() x(t)
иx(t) представляют собой
соответственно прямую и параболу,
причем, как и в алгебре, по коэффициентам
в уравнениях прямой и параболы можно
судить о расположении графика функции
относительно координатных осей.
x(t)
иx(t) представляют собой
соответственно прямую и параболу,
причем, как и в алгебре, по коэффициентам
в уравнениях прямой и параболы можно
судить о расположении графика функции
относительно координатных осей.
|
|
Рис. 6
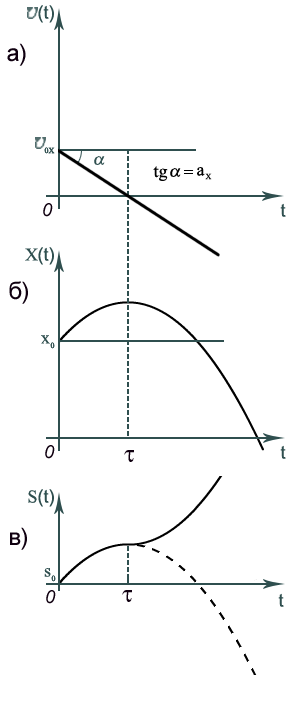
На
рисунке 6 приведены графики для x(t),![]() x(t),s(t) в случаеx0> 0,
x(t),s(t) в случаеx0> 0,![]() 0x> 0,ax< 0. Соответственно прямая
0x> 0,ax< 0. Соответственно прямая![]() (t)
имеет отрицательный наклон (tg=ax< 0).
(t)
имеет отрицательный наклон (tg=ax< 0).
3. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.
Равномерное
движение по окружностипроисходит с
постоянной по модулю скоростью, т.е.![]() =
const (рис. 7). Однако направление скорости
при таком движении непрерывно изменяется,
поэтому равномерное движение тела по
окружности является движением с
ускорением.
=
const (рис. 7). Однако направление скорости
при таком движении непрерывно изменяется,
поэтому равномерное движение тела по
окружности является движением с
ускорением.
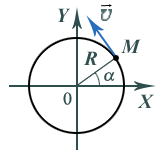
Рис. 7
Для описания равномерного движения тела по окружности вводят следующие физические величины: период,частота обращения,линейная скорость,угловая скоростьицентростремительное ускорение.
Период обращенияT– время, за которое совершается один полный оборот.
Частота обращения– это число оборотов, совершаемых телом за 1 с. Единицей частоты обращения в СИ является с–1.
Частота
и период обращения связаны между собой
соотношением
![]() .
.
|
|
Вектор скорости при движении точки по окружности постоянно изменяет свое направление (рис. 8).
При
равномерном движении тела по окружности
отрезок пути s,
пройденный за промежуток времениt,
является длиной дуги окружности.
Отношение![]() постоянно
во времени и называетсямодулем
линейной скорости.За время, равное
периоду обращенияТ, точка проходит
расстояние, равное длине окружности
2R, поэтому
постоянно
во времени и называетсямодулем
линейной скорости.За время, равное
периоду обращенияТ, точка проходит
расстояние, равное длине окружности
2R, поэтому
![]()
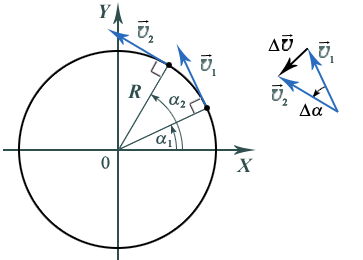
Рис. 8
Скорость вращения твердых тел принято характеризовать физической величиной, называемой угловой скоростью , модуль которой равен отношению угла поворота телак промежутку времени, за которое этот поворот совершен (рис. 8):
![]()
Единицей угловой скорости в СИ является с–1.
Так как ориентация твердого тела одинакова во всех системах отсчета, движущихся друг относительно друга поступательно, то и угловая скорость обращения твердого тела будет одинакова во всех системах отсчета, движущихся друг относительно друга поступательно.
При равномерном вращении твердого тела относительно некоторой оси любая точка этого тела движется вокруг этой же оси по окружности радиусом Rс линейной скоростью, которая равна
![]() =
R.
=
R.
Если начальные координаты точки равны (R; 0), то ее координаты меняются по законуx(t) =Rcostиy(t) =Rsint.