ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.02.2019
Просмотров: 6231
Скачиваний: 1
Обобщенная модель ядра была развита в 1950 г. в основном трудами
Рейнвотера, О. Бора и Моттельсона, Хилла и Уилера.
В ОМО Самосогласованный сферически-симметричный потенциал (ССП) -
результат взаимодействия нуклонов между собой. Он должен зависеть от
движения и взаимодействия индивидуальных нуклонов и определяются числом
нуклонов
n
сверх заполненных оболочек.
Для ядер с заполненными или почти заполненными
оболочками:
Потенциал и форма ядра при небольшом
количестве добавочных нуклонов остаются
сферически-симметричными.
Возбужденные состояния этих ядер определяются
одночастичными уровнями в ССП и квадрупольными
колебаниями относительно равновесной
сферически-симметричной формы ядра.
С ростом числа нуклонов сверх заполненных оболочек → появляется центробежное
давление избыточных нуклонов на стенки ядра.
При дальнейшем росте
n
-
сф.–сим. форма ядра может оказаться нестабильной →
V
min
соответствует несферическому ядру с равновесной деформацией, отличной от
нуля. Ядро обладает аномальным
Q
.
Обобщенная модель ядра
Квантовая механика:
У несфер. ядра должна появляться вращательная степень свободы, т. е. вращательные
спектры уровней.
Частота колебаний (энергия осцилляторных уровней) должна снизиться.
В несферическом потенциале должен измениться характер одночастичных уровней.
Система уровней несферического ядра определяется как одночастичным, так и
коллективным (вращение, колебания) движением нуклонов, находящихся вне
заполненных оболочек.
При очень сильном возбуждении ядра возможны колебания всех его нуклонов ~ 10 МэВ.
ОДНОЧАСТИЧНЫЕ СОСТОЯНИЯ В НЕСФЕРИЧЕСКОЙ ЯМЕ
В несфер. поле
(2J+1)
-
краткое вырождение уровня снимается. Eсли поле имеет осевую
симметрию,
J
z
вектора
J
на ось симметрии. Это приводит к двукратному вырождению
каждого подуровня с данным значением
|J
z
| (+J
z
и -J
z
)
. Таким образом, уровень
J
расщепляется на
(2J+1)/2,
сдвинутых относительно друг друга подуровней. Степень сдвига
зависит от знака и параметра несферичности ядра (можно оценить из значений
Q)
.
/
R R
Обобщенная модель ядра
Квантовая механика:
У несфер. ядра должна появляться вращательная степень свободы, т. е. вращательные
спектры уровней.
Частота колебаний (энергия осцилляторных уровней) должна снизиться.
В несферическом потенциале должен измениться характер одночастичных уровней.
Система уровней несферического ядра определяется как одночастичным, так и
коллективным (вращение, колебания) движением нуклонов, находящихся вне
заполненных оболочек.
При очень сильном возбуждении ядра возможны колебания всех его нуклонов ~ 10 МэВ.
ОДНОЧАСТИЧНЫЕ СОСТОЯНИЯ В НЕСФЕРИЧЕСКОЙ ЯМЕ
1955 г. Нильссон
: потенциал осциллятора с осевой симметрией и сильной
ls-
связью:
2
2
2
2
2
2
1
( )
(
)
(
)
2
Z
V r
M
x
y
z
C l s
Dl
В несфер. поле
(2J+1)
-
краткое вырождение уровня снимается. Eсли поле имеет осевую
симметрию,
J
z
вектора
J
на ось симметрии. Это приводит к двукратному вырождению
каждого подуровня с данным значением
|J
z
| (+J
z
и -J
z
)
. Таким образом, уровень
J
расщепляется на
(2J+1)/2,
сдвинутых относительно друг друга подуровней. Степень сдвига
зависит от знака и параметра несферичности ядра (можно оценить из значений
Q)
.
/
R R
ω
2
= ω
0
2
(1+2δ/3); ω
Z
2
= ω
0
2
(1-4δ/3); C, D, ω
0
– константы,
δ
–
параметр деформации
Обобщенная модель ядра
Результаты расчета:
Для сф. сим. ядра
N
нукл
(p
3/2
) = 4
при
δ=0
при
δ
≠0 p
3/2
расщепляется на два подуровня для проекций
j= 3/2:
±1/2 и ±3/2.
Четность обоих подуровней “-” (
l=1
).
При
δ
>0
сначала
должен заполняться подуровень с
j
z
=
±1/2
, а затем—
подуровень с
j
z
=
±3/2
, при
δ
< 0
-
наоборот.
6
19
21
23
3
9
10
11
,
,
,
.
Li
F
Ne
N
Ядра
и др проблемы в рам
a
ках ОМО
Все они имеют
Q>0
, т. е.
δ
= ΔR/R>0
6
3
Li
- 3-
й неспаренный
p
и 3-й неспаренный
n
→
подуровень
1/2
-
→ J=1
+
19
9
F
- 9-
й неспаренный
p
→ подуровень
1/2
+
→ J=1/2
+
23
11
Na
- 11-
й неспаренный
p
→ подуровень
3/2
+
→ J=3/2
+
Обобщенная модель ядра
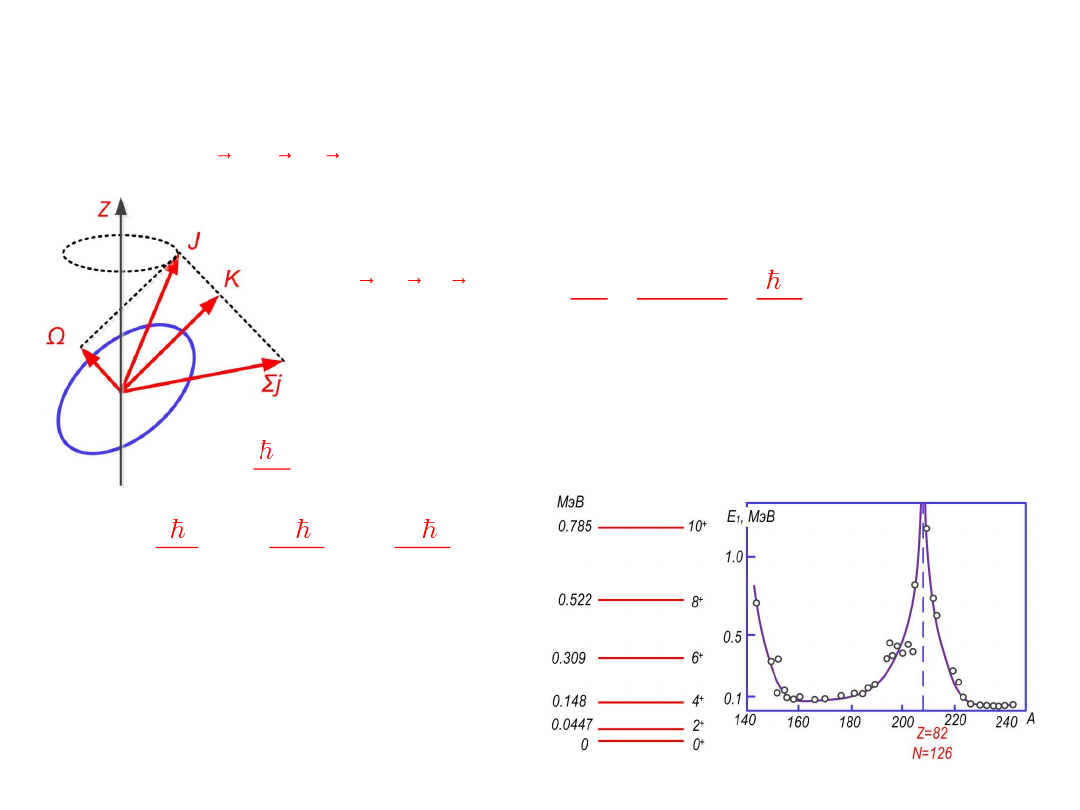
В возбужденном состоянии несфер. ядра:
J
≠J
0
т.к. изменится
∑j
и появится вращение (вращательный момент
Ω
):
ВРАЩАТЕЛЬНЫЕ СОСТОЯНИЯ
Несферическое ядро (эллипсоид вращения):
J=∑j
(
j
– проекция спина нуклона на ось
симметрии) - . для основного состояния (для ч-ч ядер
I
0
=K=0
)/
K
0
K
J
J
K
G
–момент инерции:
G≈G
0
·(ΔR/R)
2
Для ч-ч ядер для переходов в основное состояние (
K=0
)
2
2
2
2
(
1)
(
)
2
2
2
вр
J
K
E
J J
K K
K
G
G
G
J= 0, 2, 4, 6,
… из-за симметрии, т.е. четность вр. сост. +1
2
2
2
0
1
2
3
3
10
21
0;
;
;
;...
E
E
E
E
G
G
G
2
(
1)
2
вр
E
J J
G
Масштаб энергии E
1
:
(A~240)
– 40-50 кэВ
A~150
÷160 – 80-90 кэВ
Обобщенная модель ядра
238
92
U