Добавлен: 21.10.2018
Просмотров: 2685
Скачиваний: 10
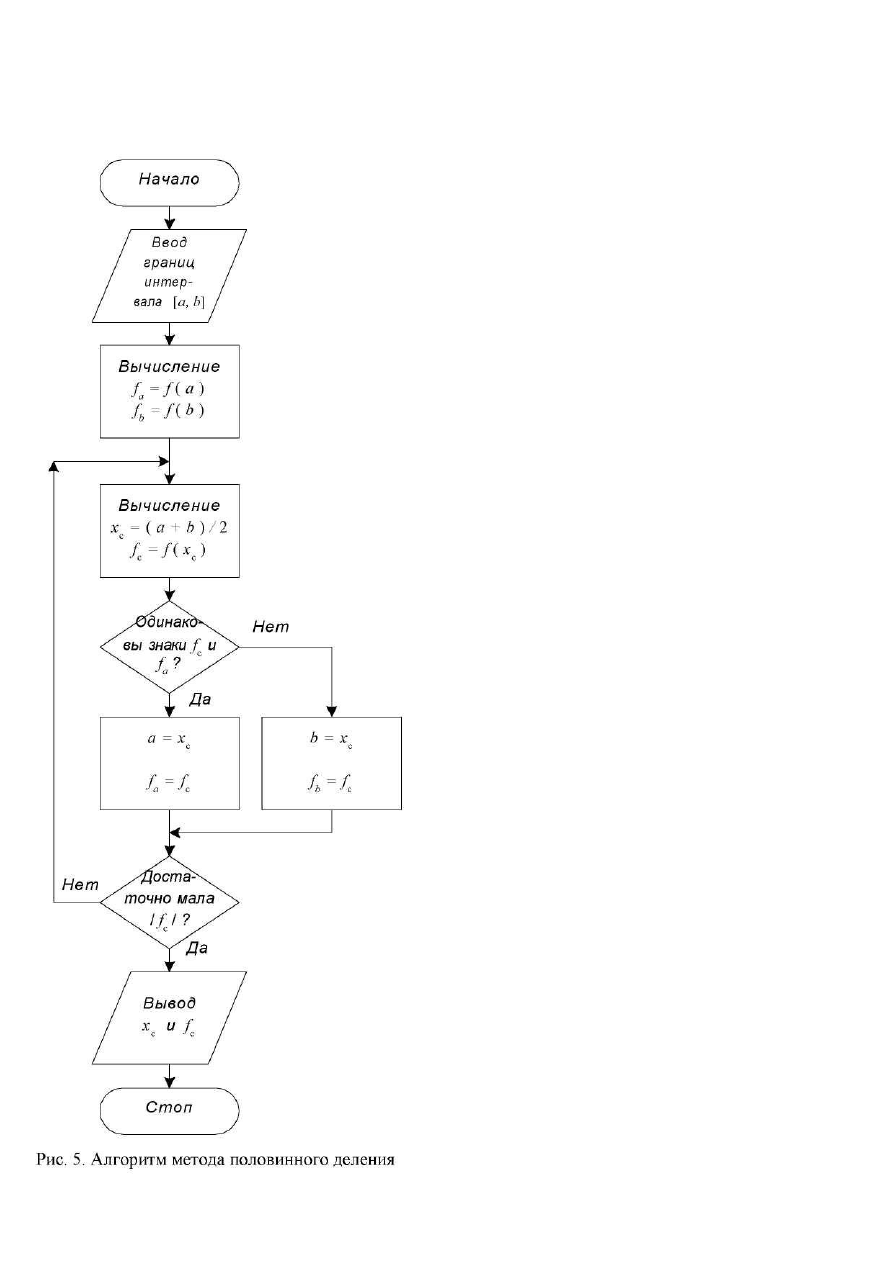
Метод включает следующие операции (см.
рис. 5). Вначале на концах исходного отрезка [a,
b], содержащего корень, вычисляют значения
функции f(a) и f(b). Затем находят точку, деля-
щую [a, b] на две равные части, по итерацион-
ной формуле
x
c
= (a+b)/ |2 (6)
и вычисляют значение функции f(x
c
). Далее по
перемене знака функции выбирают ту половину
[a, b], в которой расположен корень.
Если знаки f(x
c
) и f(a) совпадают, то в
дальнейшем полагают a = x
c
и f(a) =f(x
c
). Если же,
напротив, знаки f(x
c
) и f(a) различаются, а знаки
f(x
c
) и f(b) совпадают, то полагают b = x
c
и f(b) =
f(x
c
). В результате этих действий получают но-
вый отрезок, содержащий корень. Этот отрезок
имеет длину в два раза меньше, чем исходный.
Точно так же, как и в предыдущем случае,
если очередное рассчитанное значение f(x) дос-
таточно близко к нулю, вычисления прекраща-
ются. Иначе процесс половинного деления про-
должается.
В некоторых случаях для остановки ите-
рационной процедуры используют условие ма-
лости полученного на очередном шаге отрезка,
записывая его, например, как
| (b−a)/x
c
| ≤δ. (7)
Приняв δ = 0,01, можно таким образом получить
положение корня с точностью порядка одного процента.

Метод половинного деления позволяет заметно ускорить поиск решения
по сравнению с пошаговым поиском, рассмотренным в п. 1.3.1. Для того чтобы
оценить, каков выигрыш, вспомним, что для уменьшения длины исходного от-
резка, содержащего корень, в миллион раз в предыдущем случае потребовалось
выполнить три итерационных шага и провести вычисление f(x) в 297 новых
точках.
В то же время нетрудно подсчитать, что в методе половинного деления
для получения аналогичного результата необходимо сделать 20 шагов, так
как при N = 2 и K = 20 получается сужение в NK = 220 = 1048576 раз. А
р а сч е т ф ун к ции f (x ) д ля этого п о тре б уе тс я прове с ти ли шь в N х
20 = 1 х 20 = 20 новых точках. В итоге объем и время вычислений по сравнению
с ранее рассмотренной процедурой сокращается примерно в пятнадцать раз.
1.3.3. Метод хорд
Этот итерационный метод подобно рассмотренному выше методу по-
ловинного деления заключается в повторяющемся делении интервала на две
части с выбором из них той, которая содержит корень уравнения. Однако в ме-
тоде хорд точка, с помощью которой исходный отрезок [a, b] делится на две
части, выбирается не как средняя, а вычисляется с помощью линейной интер-
поляции функцииf(x) на [a, b].
Последовательно выполняются следующие действия. Вначале вычис-
ляются значения функции f(x) на концах отрезка в точках a и b, то есть f(a)
иf(b). После этого составляется уравнение хорды, которая представляет собой
прямую y(x), проходящую через эти две точки. Данная хорда описывается соот-
ношением
С помощью хорды на отрезке [a,b] выбирается точка x
с
, в которой
y(x
c
) = 0. Для этого подставим в (8) y(x) = y(x
c
) = 0 и получим итерационную
формулу метода хорд:
)
(
)
(
)
(
a
f
b
f
a
b
a
f
a
x
c
(9)
Точка x
c
делит отрезок [a, b] на две части. Также как и в методе половинного де-
ления из двух частей выбирается та, на краях которой функция f(x) имеет
противоположные знаки. Далее описанный процесс повторяется многократно и
может быть остановлен по условию (5) или (7).
Процесс поиска корня методом хорд показан графически на рис. 6.
a
b
a
f
b
f
a
x
a
f
x
y
)
(
)
(
)
(
)
(
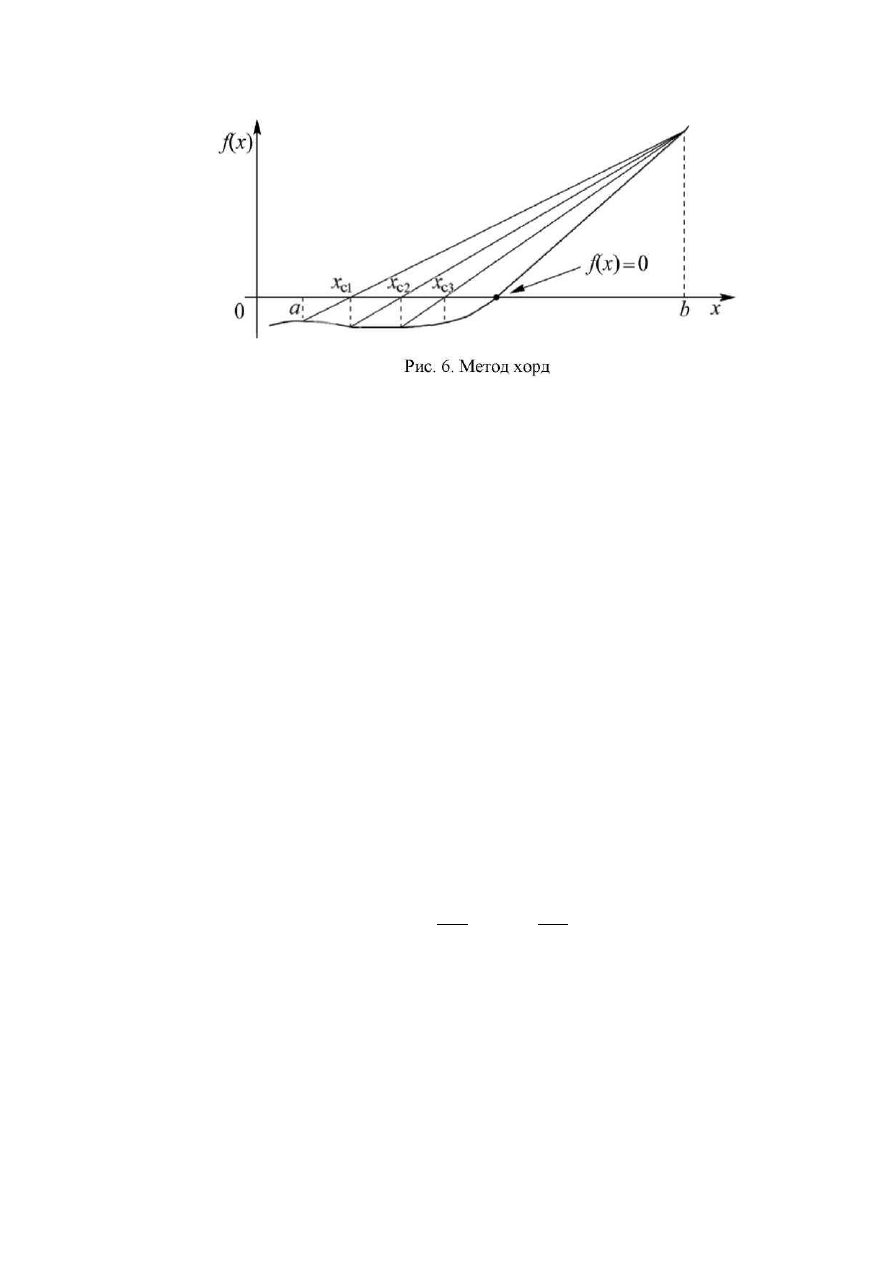
Из рисунка видно, что получаемые с помощью (9) точки x
c
постепенно
сходятся к корню уравнения. Поскольку в рассмотренном методе очередное
приближение x
c
определяется с помощью интерполяции, учитывающей наклон
кривой f(x), он во многих случаях оказывается более эффективным, чем метод
половинного деления.
Алгоритм решения методом хорд имеет вид аналогичный алгоритму ме-
тода половинного деления, приведенному на рис. 5 и отличается только видом
итерационной формулы, по которой рассчитывается x
c
.
1.3.4. Метод Ньютона (метод касательных или метод линеаризации)
Этот метод в отличие от ранее рассмотренных не требует предварительно
указывать интервал, в котором располагается корень уравнения. Для начала ра-
боты требуется задать лишь одну начальную точку x
0
, расположенную вблизи от
предполагаемого корня. Направление поиска определяется из этой точки с по-
мощью линейной экстраполяции f(x). Таким образом, при начале расчета из за-
данной точки x
0
определяется точка х
ь
затем из точки x1 рассчитывается x
2
и так
далее. Продолжение этого процесса далее дает последовательность чисел x
0
, x
1
,
x
2
, x
3
..., x
i
... последовательно приближающихся к корню уравнения.
Для получения итерационной формулы метода Ньютона воспользуемся
разложением функции f(x) в окрестности точки x
i
в ряд Тейлора:
,
...
)
(
'
'
'
!
3
)
(
''
!
2
)
(
'
)
(
)
(
3
2
i
i
i
i
i
x
f
x
x
f
x
x
xf
x
f
x
x
f
(10)
uде f’(x
i
), f”(x
i
) и f”’(x
i
) - первая, вторая и третья производные от функ
ции
f(x) по x.
Сократим (10), отбросив слагаемые, содержащие Δх во второй и более вы-
соких степенях. Тогда
f(x
i
+Δx)≈f(x
i
) + f(x
i
)∙Δx .
Полагая далее, что в окрестностях x
i
имеется точка x
i+1
= x
i
+ Δх, в которой
функция
)
(
)
(
1
x
x
f
x
f
i
i
равна нулю, получим линейное уравнение
0
)
(
'
)
(
x
x
f
x
f
i
i
,
из которого найдем x
i+1
)
(
'
/
)
(
1
i
i
i
i
x
f
x
f
x
x
.
(11)
Это соотношение является итерационной формулой метода Ньютона.
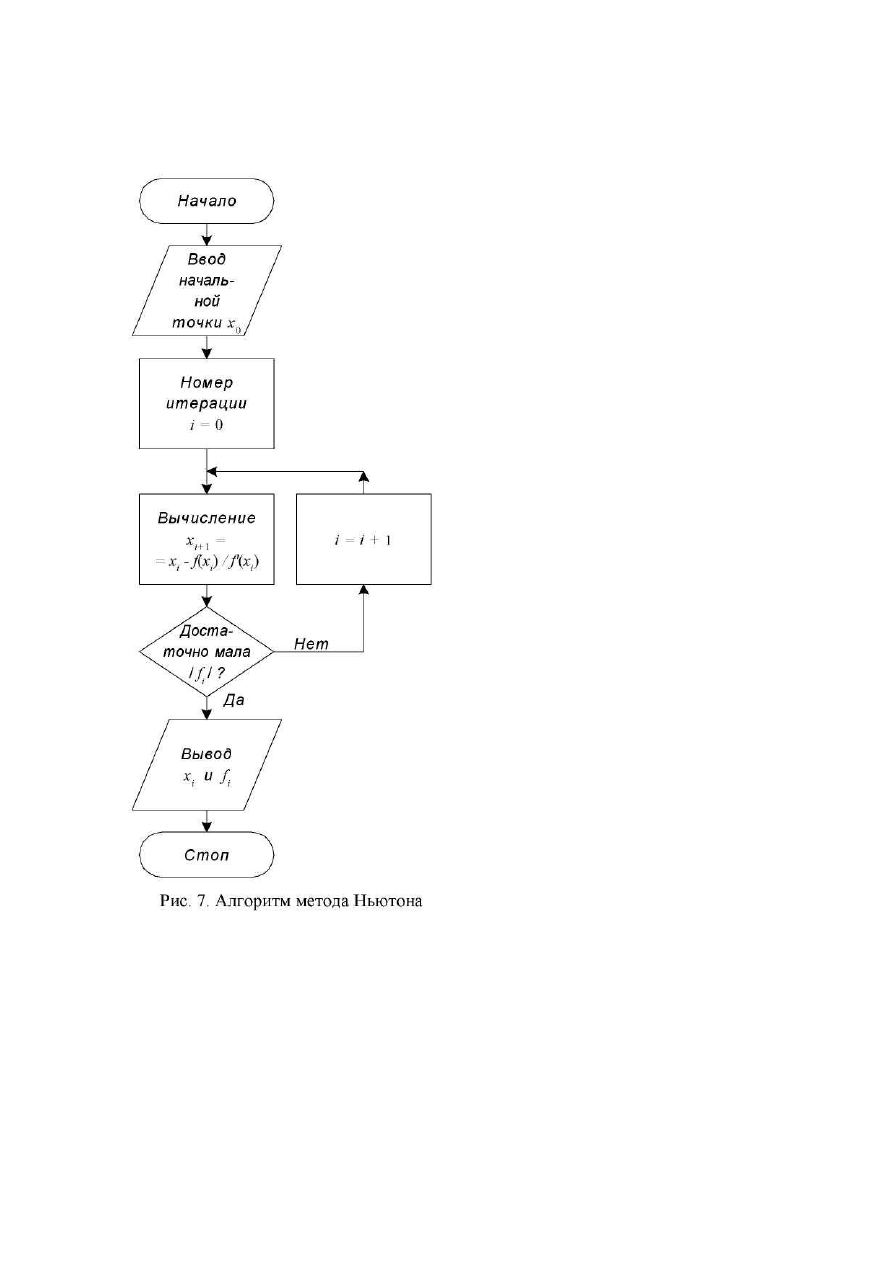
Алгоритм метода Ньютона пред-
ставлен на рис. 7.
Получаемые методом Ньютона точки
x
i
образуют ряд чисел x
0
, x
1
,x
2
, x
3
, ..., кото-
рый сходится к точному решению, то есть к
корню уравнения.
Из (11) следует, что каждый шаг ме-
тода Ньютона требует большего объема
вычислений чем, например, метод половин-
ного деления, так как приходится находить
значение не только функции f(x), но и ее
производной. Несмотря на это метод Нью-
тона и его модификации широко использу-
ются на практике.
Это обусловлено, во-первых, тем, что
он не требует задания отрезка [a, b],
содержащего корень, а может стартовать от
одной начальной точки. Во-вторых, он
имеет более высокую скорость сходимости,
чем ранее рассмотренные методы.
Теоретически можно показать, что
метод Ньютона позволяет получить квадра-
тичную сходимость. Это означает, что на
каждой итерации погрешность (отклоне-
ние очередного приближения x
i
от точного
решения) уменьшается по квадратичному
закону, то есть количество верных знача-
щих цифр решения удваивается.
Если на очередном шаге достиг-
нута погрешность не более 0,5 то за
пять-шесть итераций она уменьшится до
величины порядка 2
-64
, что сопоставимо с
погрешностью вычислений на ЭВМ. В
методе половинного деления для достижения такой же погрешности количе-
ство итераций потребовалось бы увеличить более чем на порядок.
На рис. 8, а представлен ход решения методом Ньютона в графиче-
ском виде.
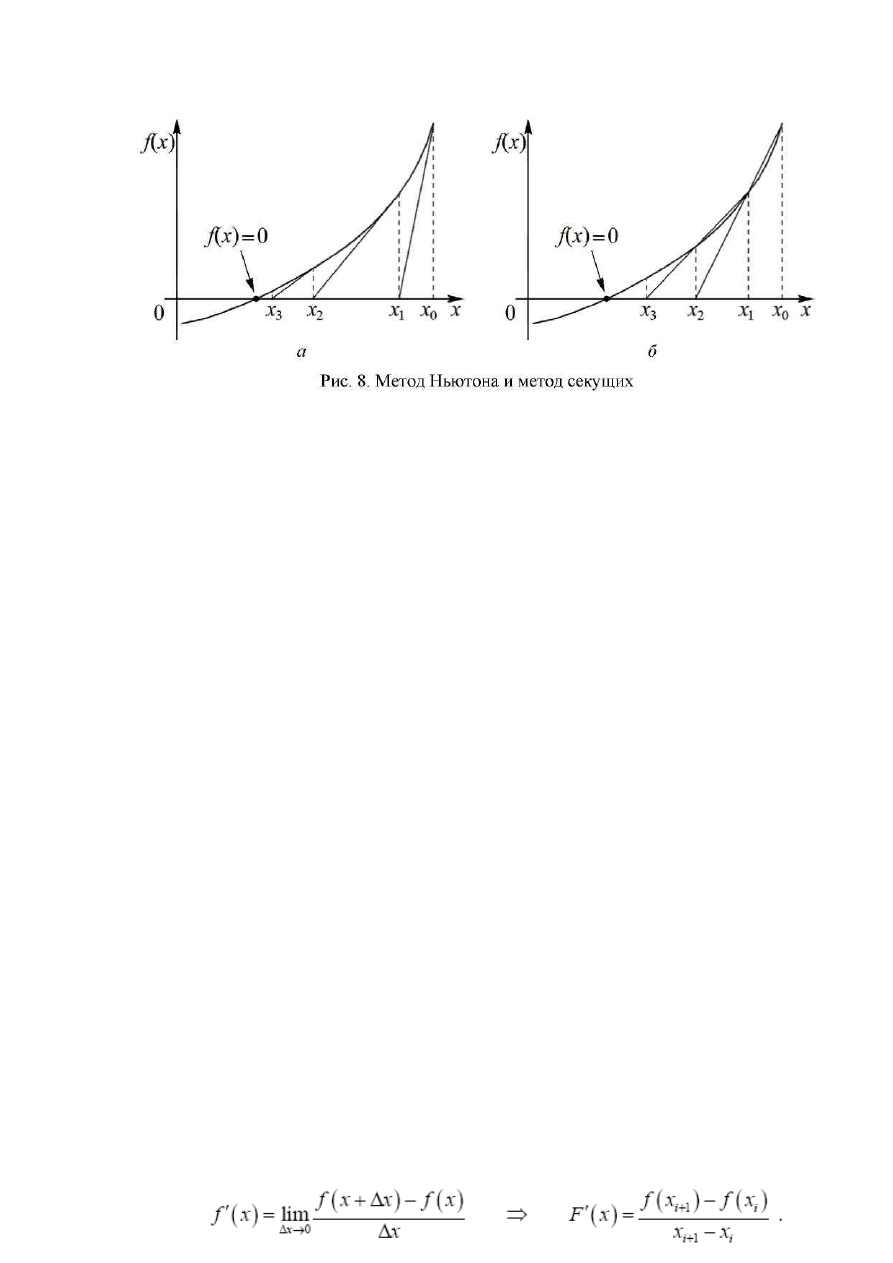
При использовании метода Ньютона следует учитывать ряд его осо-
бенностей. Одна из них состоит в необходимости правильного выбора на-
чального приближения. Чтобы понять, как влияет выбор начальной точки
на работу метода, попробуйте графически найти решение для рис. 8, начав
его из точки X
0
= a.
Метод Ньютона обладает локальной сходимостью, то есть способен
найти корень, если начальное приближение задано в некоторой малой его
окрестности. Если же начальное приближение взято неудачно и функция
немонотонна, метод может дать расходящуюся последовательность x
i
(см. п.
1.5).
Другая проблема заключается в том, что производная f'(x) в (11) на-
ходится в знаменателе. Это означает, что f'(x) не должна обращаться в
ноль, так как в противном случае итерационная формула перестает работать.
Трудности могут возникнуть и в том случае, если f'(x) не равна нулю, но
достаточно мала, вследствие чего результат деления f(x)/ f'(x) может
оказаться
неприемлемо большим.
Во многих математических пакетах, например, в MathCAD и MATLAB
эти проблемы решаются применением комбинированных алгоритмов, соче-
тающих достоинства различных методов, например, метода половинного
деления и метода Ньютона. Первый обеспечивает устойчивую сходимость и
используется на начальном этапе решения, а после некоторого числа итера-
ций включается второй, быстрее приближающийся к корню уравнения.
1.3.5. Метод секущих
Производная f'{x) в методе Ньютона может быть найдена аналитически
дифференцированием функции f(x). Однако это усложняет подготовительный
этап к решению уравнения.
На практике часто используют модификации метода Ньютона, свободные
от этого недостатка. Одно из упрощений сводится к тому, что производная вы-
числяется только один раз в начальной точке и затем это значение используется