Добавлен: 21.10.2018
Просмотров: 2687
Скачиваний: 10

на всех последующих шагах. Данная модификация основывается на предполо-
жении о малом изменении производной вблизи корня.
Одной из наиболее известных модификаций является метод секущих. В
этом методе производная заменяется ее приближенным значением:
В формуле для F ' ( x ) в отличие от f'(х) приращение Δx = x
i+1
– x
i
полагается
малым, но Δх ≠ 0. Геометрическая иллюстрация метода при Δх < x
i
показана на
рис. 8, б. В случае более жесткого условия Δх « х
i
секущие на рис. 8, б практи-
чески совпадут с касательными к кривой (см. рис. 8, а).
Алгоритм решения методом секущих аналогичен алгоритму метода Нью-
тона, приведенному на рис. 7 и отличается только видом итерационной форму-
лы, по которой рассчитываются x
i
.
Метод секущих также как и метод Ньютона имеет сверхлинейную, то есть
приближающуюся к квадратичной сходимость.
1.3.6. Метод простой итерации
Метод простой итерации основывается на приведении исходного уравнения
f(x) = 0 к следующему виду: x = ψ(x). При этом процесс последовательного при-
ближения к корню строится на основе итерационной формулы
)
(
1
i
i
x
x
Очевидно, получить расчетную формулу можно, используя следующую
цепочку преобразований:
где b — некоторый не равный нулю сомножитель.
На рис. 9 приведены графические иллюстрации, показывающие при-
ближение к корню в методе простой итерации.
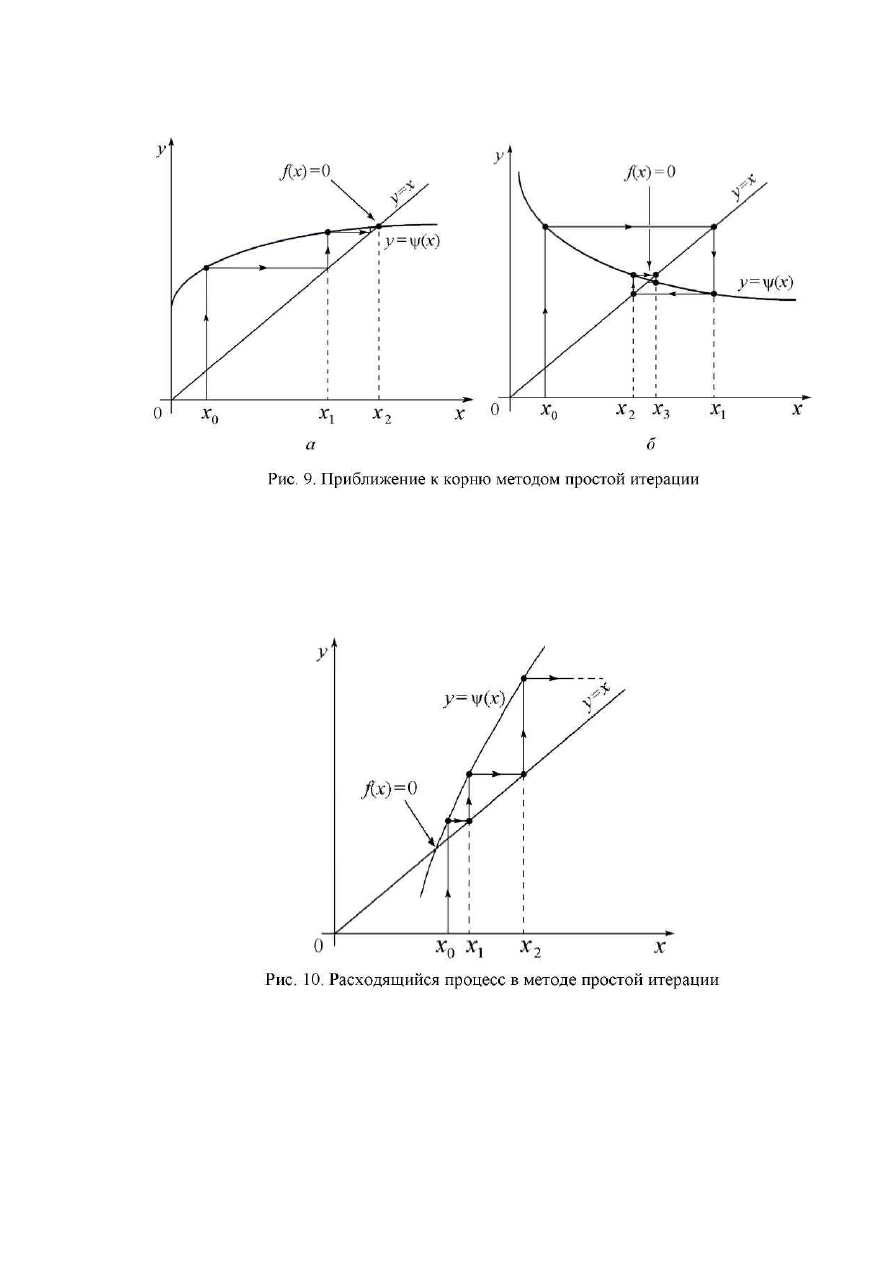
Сходимость процесса приближения к корню в значительной степени
определяется видом зависимости ψ (x). На рис. 9 показаны сходящиеся про-
цессы, а на рис. 10 - расходящийся. В последнем случае метод простой ите-
рации не находит решения уравнения. Существенное влияние на сходимость
оказывает выбор коэффициента b - сравните, например, рис. 9, а и рис. 10.
На рис. 9 сходимость обеспечивается для медленно изменяющихся
функций ψ (x), для которых выполняется условие | ψ ' (x) | < 1. На рис. 10 рас-
ходящийся процесс наблюдается для более быстро меняющейся функции
|ψ ' (x) | > 1. Можно сделать вывод, что для обеспечения сходимости метода
простой итерации необходимо выполнить условие | ψ ' (x) | < 1.
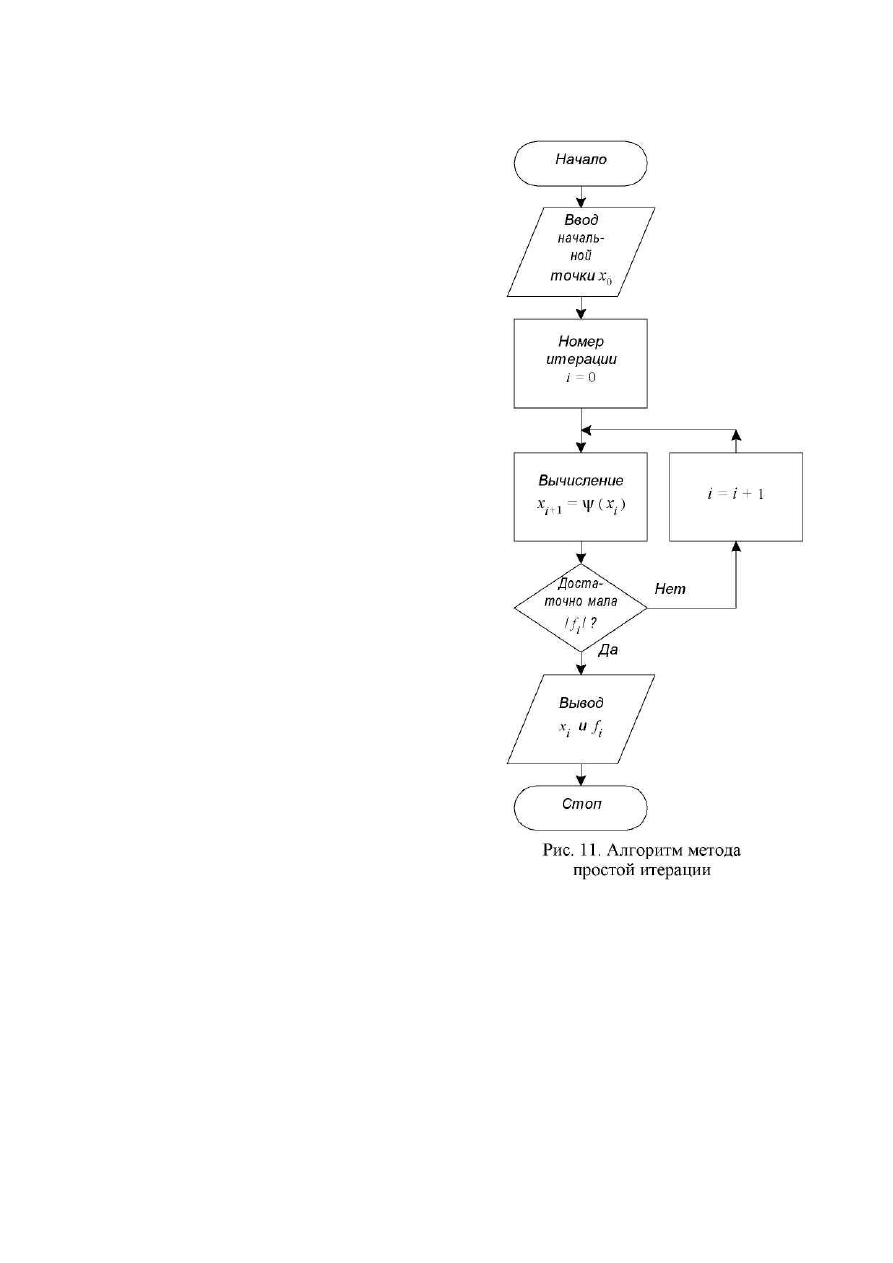
Алгоритм метода простой итерации приведен на рис. 11.
Теоретически можно показать,
что высокая скорость сходимости обес-
печивается при b = -1/ f'(x).
В этом случае метод простой итерации
эквивалентен методу Ньютона.
Вообще говоря, если в методе
Ньютона производная f'{x) каждый
раз вычисляется на очередном шаге,
то в методе простой итерации для опре-
деления b можно вычислить про-
изводную в начальной точке X
0
И ПОТОМ
сохранять параметр b = -1/f'{x)
неизменным. Такой метод, называемый
иногда упрощенным методом Ньютона,
был рассмотрен в п. 1.3.5.
1.3.7. Методы, использующие не-
линейную интерполяцию
Существует группа численных
методов, являющихся развитием идеи
метода Ньютона. Как правило, они ис-
пользуют различные виды парабо-
лической интерполяции.
Различие алгоритмов этих мето-
дов определяется способом построения
параболы. Например, в методе Мюлле-
ра вначале необходимо вычислить
три исходные точки
(x
0
, f(x
0
)), (x
1
, f(x
1
)) и (x
2
, f(x
2
)).
По данным трем точкам строится па-
рабола, аппроксимирующая f(x).
После этого очередное приближе-
ние x
i+1
определяется как корень квад-
ратного уравнения, соответствующего параболе. Многократное повторение
процедуры обеспечивает последовательное приближение решению.
1.3.8. Методы решения алгебраических уравнений
Для алгебраических уравнений вида (2):
разработаны специальные методы решения. При отыскании корней алгеб-
раических уравнений необходимо учитывать следующие их свойства.
1. Алгебраическое уравнение порядка n имеет n корней, которые могут
быть действительными или комплексными.
0
...
4
4
3
3
2
2
1
0
n
n
x
a
x
a
x
a
x
a
x
а
а

2. Если все коэффициенты a
i
действительные, то все комплексные кор
ни образуют комплексно-сопряженные пары.
3. Число положительных действительных корней равно или меньше
перемен знаков в последовательности коэффициентов ai.
4. Число отрицательных действительных корней равно или меньше пе
ремен знаков в последовательности коэффициентов a
i
при замене x на —x.
Специальные методы решения алгебраических уравнений обычно сво-
дятся к понижению их порядка. Обычно из функции f(x) в левой части урав-
нения выделяется сомножитель в виде квадратного уравнения:
0
)
...
)(
(
2
2
3
3
2
2
1
0
2
n
n
x
b
x
b
x
b
x
b
b
q
px
x
При этом порядок второго сомножителя снижен на 2 относительно ис-
ходного уравнения. Из квадратного уравнения находят два корня по известной
формуле, а с оставшимся сомножителем вновь повторяют описанную процеду-
ру понижения порядка.
Основной трудностью в данном способе решения является разделение
f(x) на сомножители без остатка. Для этого используют специальные итера-
ционные процедуры, позволяющие подбирать приближенные значения ко-
эффициентов p, q, b
0
, b
1
, b
2
, ..., b
n
в обоих сомножителях.
Недостатком подобных методов является то, что по мере понижения по-
рядка уравнения накапливается ошибка, обусловленная неточным определение
коэффициентов сомножителей. В итоге последние из найденных корней будут
определены с наибольшей погрешностью.
1.4. Источники погрешности решения задачи на ЭВМ
Рассмотренные итерационные методы поиска корней нелинейных урав-
нений по своей природе являются приближенными в отличие от прямых мето-
дов, дающих точное решение. С точки зрения точности результата ис-
пользование прямых методов может показаться более предпочтительным. Од-
нако на самом деле при решении задачи на компьютере ответ все равно будет
содержать погрешность.
В качестве основных источников погрешности обычно рассматривают
три вида ошибок. Это так называемые ошибки усечения, ошибки округления и
ошибки распространения. Рассмотрим их.
1.4.1. Ошибки усечения
Этот вид ошибок связан с погрешностью, заложенной в самой задаче. Он
может быть обусловлен неточностью определения исходных данных. На-
пример, если в условии задачи заданы какие-либо размеры, то на практике
для реальных объектов эти размеры известны всегда с некоторой точно-
стью. То же самое касается любых других физических параметров. Сюда же
можно отнести неточность расчетных формул и входящих в них числовых

коэффициентов.
Большое число расчетных формул являются эмпирическими и дают
результат с некоторой погрешностью, содержат подгоночные коэффициен-
ты, обеспечивающие приемлемую ошибку в ограниченном диапазоне
входных параметров. Поэтому, как правило, если исходные данные извест-
ны с некоторой погрешностью, вряд ли стоит пытаться получить результат
с меньшей погрешностью.
1.4.2. Ошибки распространения
Данный вид ошибок связан с применением того или иного способа
решения задачи. В ходе вычислений неизбежно происходит накопление
или, иначе говоря, распространение ошибки. Помимо того, что сами ис-
ходные данные не являются точными, новая погрешность возникает при их
перемножении, сложении и т. п. Накопление ошибки зависит от характера
и количества арифметических действий, используемых в расчете.
Обычно для решения одной и той же задачи может быть использо-
ван ряд различных методов решения. Например, систему линейных алгеб-
раических уравнений можно решить методом Гаусса или через определи-
тели (методом Крамера). Теоретически оба метода позволяют получить
точное решение. Однако на практике при решении больших систем урав-
нений метод Гаусса обеспечивает меньшую погрешность, чем метод Кра-
мера, так как использует меньший объем вычислений.
1.4.3. Ошибки округления
Это тип ошибок связан с тем, что истинное значение числа не всегда
точно сохраняется компьютером. При сохранении вещественного числа в
памяти компьютера оно записывается в виде мантиссы и порядка, пример-
но так же, как отображается число на дисплее калькулятора (см. рис. 12).
Здесь R
1
, R
2
, R
3
... R
n
- разряды мантиссы, D
1
, D
2
,.,, D
m
- разряды по-
рядка. На самом деле конечно, в отличие от дисплея калькулятора, ман-
тисса и порядок числа, включая их знаки, в памяти компьютера хранятся в
двоичном виде. Но для обсуждения природы ошибок округления это раз-
личие не столь принципиально.
Понятно, что иррациональные числа такие, как π =
3,14159... и e= 2,712... не могут быть представлены в памяти компью-
тера в принципе. Однако же и рациональные числа, если количество их
значащих цифр превышает число отведенных разрядов мантиссы (см.
рис. 12), будут представлены не точно. При этом цифра последнего со-
храняемого в ЭВМ разряда может быть записана с округлением или
без него.