Добавлен: 21.10.2018
Просмотров: 2688
Скачиваний: 10
Фактически при заданной структуре хранения числа компьютер
может использовать не бесконечное, а конечное число рациональных
чисел, которые вписываются в приведенную на рис. 12 схему. Поэтому
любой входной параметр решаемой задачи, ее промежуточный резуль-
тат и окончательной ответ всегда округляются до разрешенных в ком-
пьютере чисел.
Следующий важный вывод касается диапазона представления чи-
сел в ЭВМ. Если проводить рассуждения для десятичной системы счис-
ления, то максимальное по модулю число, которое может быть пред-
ставлено в соответствии со схемой на рис. 12, равно
±Х
∞
= ±999 ... 9 х 1 0
+ 9 9
-
9
.
Все числа, превышающие по модулю Х
ж
, не представимы в ЭВМ и рас-
сматриваются как машинная бесконечность. Если в ходе расчетов будет
получен результат, превышающий Х
ж
, то произойдет аварийное заверше-
ние вычислений по переполнению. Нетрудно убедиться опытным путем,
что, например, в MathCAD верхний диапазон чисел соответствует Х
ж
~
10
307
.
Минимальное по модулю число, сохраняемое в памяти компьюте-
ра, по схеме на рис. 12 равно
±X
∞
= ±000 ... 1×10
-99
...
9
.
Числа, модуль которых меньше X
0
, воспринимаются ЭВМ как нуль,
точнее как машинный нуль. Если при выполнении расчетов будет полу-
чен результат меньше, чем X
∞
, то это будет воспринято как потеря по-
рядка. Обычно в подобной ситуации результат полагается равным ну-
лю, и вычисления продолжаются.
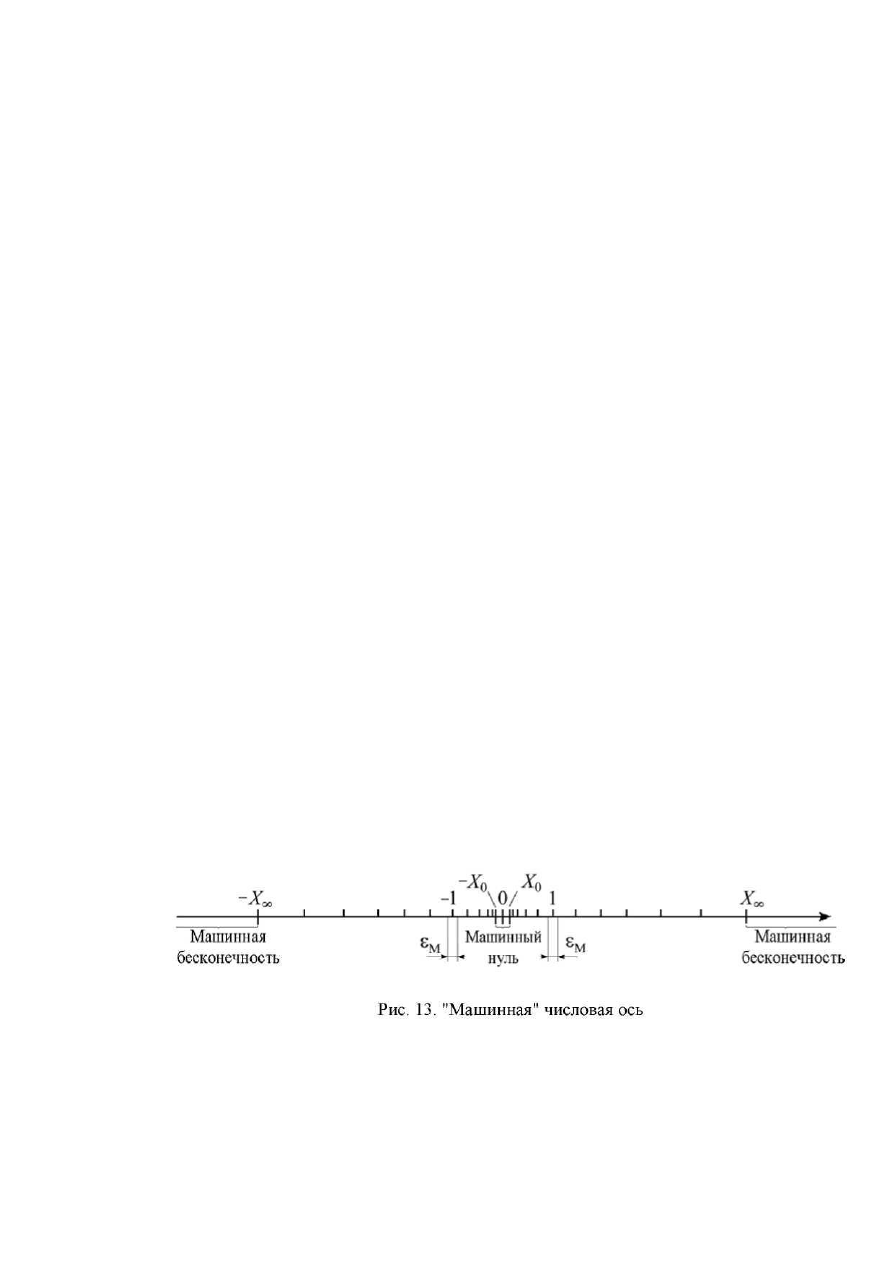
На рис. 13 показана "машинная" числовая ось, на которой от-
мечены X
0
иХ
∞
. Числа располагаются на оси неравномерно. Их плот-
ность возрастает по мере приближения к нулю.
На рис. 13 вблизи единицы отмечена небольшая область е
м
, которую на-
зывают машинное эпсилон. Параметр ε
M
весьма важен, так как он характеризует
относительную точность представления чисел в компьютере. В зависимости от
способа округления чисел в ЭВМ величина ε
M
определяется первым отбра-
сываемым или последним сохраняемым разрядом мантиссы.
Следует иметь ввиду, что длина мантиссы в памяти компьютера уста-

навливается программно. Например, при выполнении расчетов на языке
ФОРТРАН с использованием "обычной" точности (двоичная запись числа дли-
ной четыре байта) ε
M
~ 10
-7
. При удвоенной длине мантиссы ε
M
~ 10
-16
.
1.5. Использование специализированных
математических пакетов
В настоящее время широко известны специальные математические па-
кеты, облегчающие решение задач на компьютере. Это, например, системы
MATLAB и MathCAD, ориентированные на решение широкого круга мате-
матических задач. Они имеют удобный дружественный интерфейс, объектно-
ориентированный язык, набор элементарных математических и специальных
функций, встроенные графические средства. Рассмотрим их применение для
решения нелинейных уравнений.
1.5.1. Поиск корней нелинейных уравнений в MathCAD
Благодаря встроенным функциям root, Find и Minerr система MathCAD
обеспечивает получение готового решения уравнений без составления про-
граммы. Однако не во всех случаях результат может оказаться верным, даже
при отсутствии видимых ошибок. Ниже рассматриваются примеры решения за-
дач в MathCAD, обсуждаются вычислительные проблемы и способы их преодо-
ления.
MathCAD освобождает пользователя от необходимости программиро-
вания алгоритма решения уравнений. Однако основной принцип работы в
MathCAD - решение без программирования - имеет помимо очевидных дос-
тоинств и обратную сторону: неуверенность в результате вычислений. Эта не-
уверенность объясняется тем, что процесс решения скрыт от пользователя и не
может быть проконтролирован непосредственно. Примеры вычислений с оши-
бочным результатом приведены ниже.
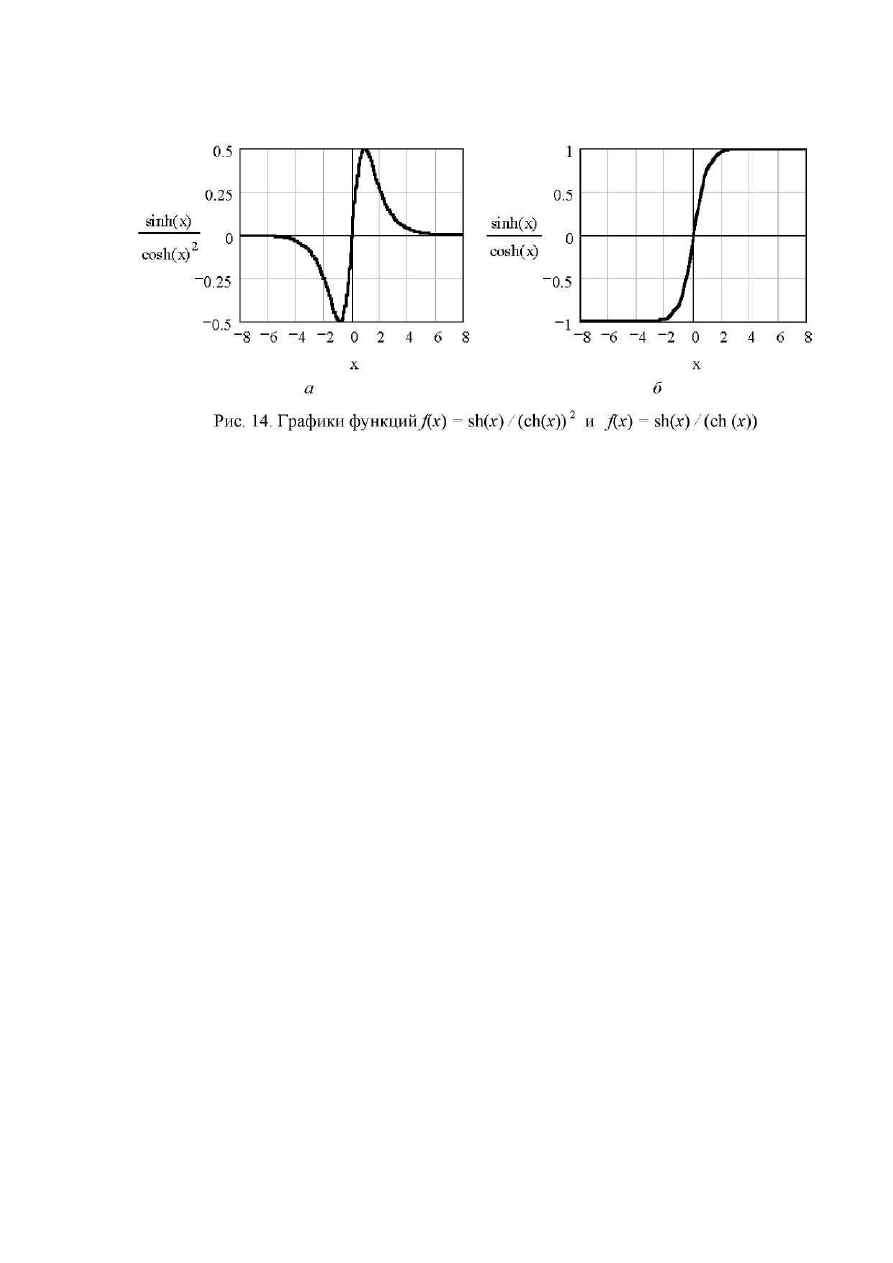
Зададим функцию, содержащую гиперболические синус и косинус: f(x)
= sh(x) / (ch(x))
2
. График этой функции в интервале -8 < x < 8 представлен на рис.
14, а.
Корнем этой функции является x = 0. Слева и справа от этой точки f(x)
имеет минимум и максимум, а при удалении от начала координатf(x) при-
ближается к нулю. С формальной точки зрения решение уравнения f(x)
= 0 не должно вызывать проблем, поскольку функция не содержит разрывов и
имеет один корень во всей области определения неизвестного
-∞<x<+∞
При начальном приближении x = -0,5 процедура root довольно уверенно
определяет значение корня:
x:= -0.5 f(x):=sinh(x)-(cosh(x))
-2
root(f(x),x) = -7.351xl0
-7
Однако сравнительно небольшое изменение начальной точки - до х
= -0,7 приводит к заведомо неверному результату. Причѐм с увеличением тре-
бований к точности (параметр TOL) результаты удаляются от корня:
х := -0.7 TOL := 10~
3
root(f(x),x) = 7.829
х := -0.7 TOL := 10"
6
root(f(x),x) = 14.958
x := -0.7 TOL := 10"
9
root(f(x),x) = 21.89
Причина ошибок кроется как в характере зависимостиf(x), так и в особенно-
стях работы процедуры, обеспечивающей решение.
При начальном приближении x = -0,7 алгоритм root (в основу которого
положен метод секущих) попадает на внешний правый по отношению к х
= 0 склон зависимости f(x) (см. рис. 14, а) и "скатывается" по этому склону в
поисках нуля f(x) в сторону +∞. Это видно по возвращаемым функцией root
числам. Очевидно, что результаты решения неверны.
Однако система не выдаѐт никаких сообщений об ошибке. Это объясняется
тем, что MathCAD считает корнем не то значение x, при котором f(x) точно равна
нулю, а то, при котором f(x) не превышает значения системной переменной TOL,
равной по умолчанию 10
-3
. Данное условие во всех трѐх случаях выполняется. С
увеличением требований к точности расчѐта (то есть с уменьшением TOL) воз-
вращаемые root числа все больше отклоняются от корня x = 0, так как с ростом | x |
функция f(x) приближается к нулю.
Расчѐты при различных начальных значениях x показывают, что границы
области сходимости в рассматриваемой задаче примерно соответствуют усло-
вию | x | < 0,6. Аналогичный результат дает альтернативная запись решения ме-
тодом Ньютона.

Newton(f,-0.5) = -3.383x 10
-11
Newton(f,-0.7) = 36.032
Для успешного решения уравнения необходимо правильно выбирать не
только начальное приближение, но и критерий точности расчѐта. Иллюстрацией
этого служит пример решения модифицированного уравнения, отличающегося
от рассмотренного множителем 10
-3
:
x:=-0.5 TOL := 10
-3
root(f(x)-10
-3
,x) = 0.307
Корни исходного уравнения f(x) = 0 и нового fх∙10
-3
= 0 должны сов-
падать. Однако MathCAD выдаѐт неверный результат. Эта ошибка объясняется
тем, что функция fх∙10
-3
при любых значениях x не превышает значения пара-
метра TOL. Чтобы получить разумный результат, необходимо скорректировать
требования к точности, выбрав, например, TOL = 10
-6
. В этом случае MathCAD
возвращает x = -7,35117-10
-7
.
В ряде случаев особенности уравнения могут привести к неработоспо-
с о б н о с ти а л го р и т ма п о и с к а к о р н я . На п р и м е р , д л я ур а вн е н и я f(x)
= sh(x) /(ch(x)) будет выдано следующее сообщение:
x : = 2 TOL:=10 rootsinh(x)(sinh(x)),x=-3-1 =
Found a number with a magnitude greater
than 10
A
307 while trying to evaluate
this expression _______________________
Неудача объясняется тем, что функция имеет пологие участки слева и
справа от точки x = 0 (см. рис. 14, б). Поскольку алгоритм root на каждом ите-
рационном шаге делит значения функции f(x) на численный эквивалент еѐ про-
изводной, возникает переполнение (overflow), так как производная f’(х)
при | x | ≥ 2 близка к нулю.
Опасность ошибок, подобных рассмотренным выше, состоит в том, что они
могут остаться незамеченными, поскольку MathCAD не выдаѐт никаких преду-
преждающих сообщений. Поэтому при решении уравнений желательно придер-
живаться следующих правил. Во-первых, необходимо сначала провести отделе-
ние корней уравнения. Во-вторых, желательно выполнить поиск решения не-
сколько раз от различных начальных точек. Решение следует подвергать
проверке, если его правильность не очевидна.
1.5.2. Поиск корней нелинейного уравнения в MATLAB
В MATLAB реализована процедура поиска корней уравнения в виде функ-
ции fzero, использующей комбинацию методов половинного деления, секущих и
обратной квадратичной интерполяции (в версиях до 4.Х использовалась процеду-
f(x) := f(x) := sinh(x)-(cosh(x))
-2
Newton(f,x) := for i
0..1000
ра ZEROIN). Обращение к функции можно записать в виде
X1 = fzero (FUN,X0,OPTIONS) ,
где FUN - строка, содержащая имя действительной функции f(x) действительной пе-
ременной x, X0 - начальное приближение x, OPTIONS - опции решения. Если
структура OPTIONS пропущена или заменена пустой матрицей [ ], используются
установленные по умолчанию настройки процедуры решения.
Поскольку имя функцииf(x) указывается как строчная переменная FUN,
оно должно быть заключено в апострофы или выделено символом @. Н а -
п р и м е р , д л я ф у н к ц и и f ( x ) = s i n ( x ) п о с л е в в о д а с т р о к и X=f
zero ( ' sin ' , 3 ) возвращается результат X=3 . 1 41 5 9 . . . . Любая более
сложная функция f(x), для которой требуется найти корень, может быть задана с
помощью m-файла.
Рассмотрим задачу, представленную в демонстрационных примерах па-
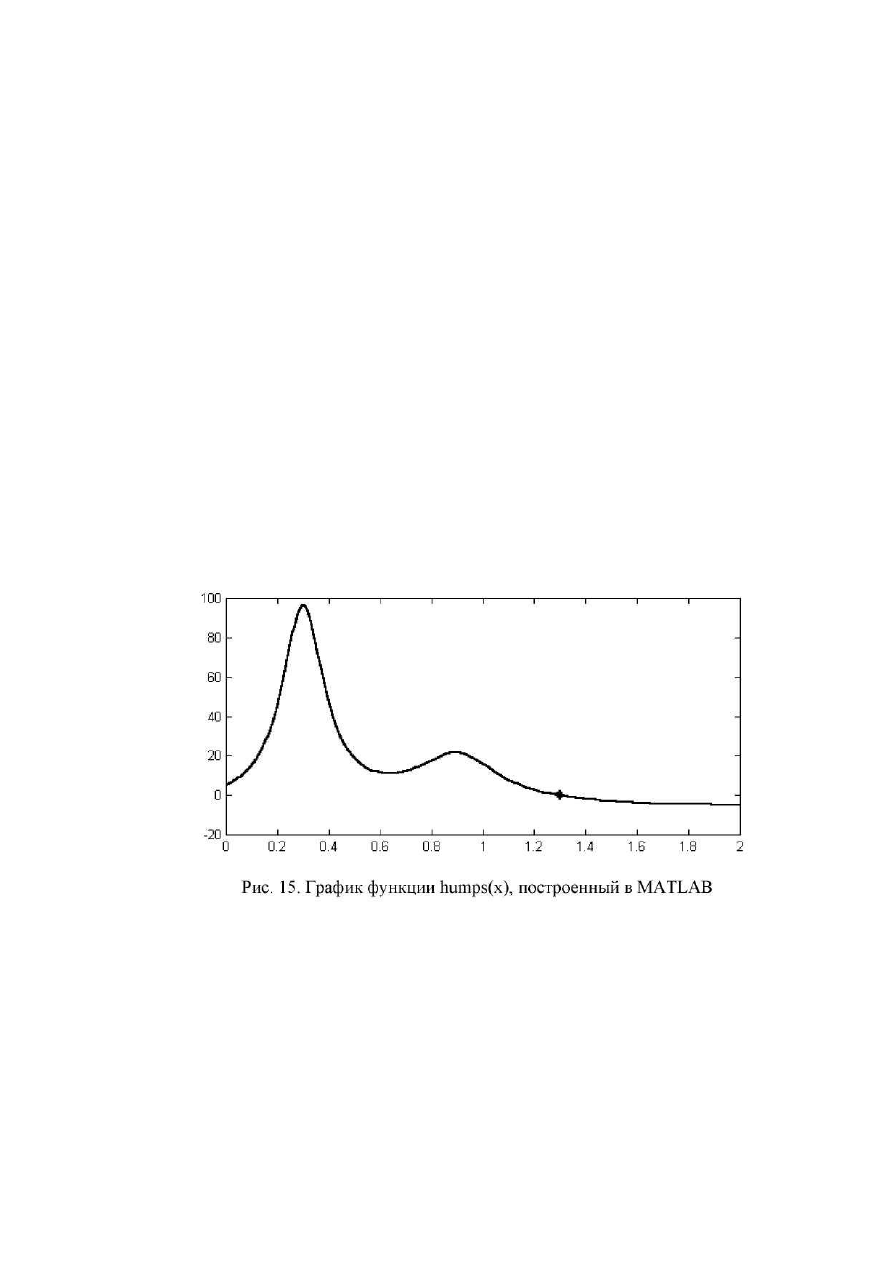
кета MATLAB. Решение отыскивается для тестовой функции humps(x), за-
писанной в файле humps.m в виде
y = 1 . 0 / (( x - 0 . 3 ) .
^
2 + 0 . 0 1 ) + 1 . 0 / ( ( х - 0 . 9 ) .
^
2 + 0 . 0 4 ) - 6 .
Графический анализ (см. рис. 15) показывает, что данное уравнение име-
ет корень вблизи x = 1,3.
Уточнение второго корня с помощью функции fzero выполняется при на-
чальном приближении x = 1.0:
X = f z e r o ( @ h u m p s , 1 . , O P T I M S E T ( ' D i s p l a y ' , ' i t e r ' ) )
Поскольку в наборе опций OPTIMSET задан параметр iter, на экран вы-
водятся промежуточные значения расчѐтных параметров. При этом выходная
переменная x принимает следующие значения:
X = 1.0; 0 . 9 7 1 7 ; 1 . 0 2 8 3 ; 0 . 9 6 ; 1 . 0 4 . . . 1 . 2 9 9 5 5 .
Последнее число, соответствующее корню уравнения, выводится на два-
дцать втором шаге решения. Заключительные пять шагов используют ин-
терполяционную процедуру - они отмечены словом "interpolation".