Файл: PIT_Metodichka_po_peredatochnym_funktsiam.pdf

Из уравнений (7.43) и  (7.45) следует 

>/2

А   = ' У ' / 2- 

(7.46)

Подставим  математическою  зависимость  (7.46) в уравнение (7.44): 

у/2  Ля7 ,  

Л - У , 

„

Т - г .  

(7  47)

^ 

Г   Г  

Г   Г

После преобразования уравнения (7.47)

2 + У2  К ^ 2

2 

Г Г

(7.48)

Подставим зависимость (7.48) в зависимость (7.38):

' ■ 4 # -

I [одставим зависимость (7.48) в зависимость (7.41):

2

2

( ’

у

- 4 - ( З

л

/ 2 - 4  

(7.50)

Таким образом,  при выполнении условий  (7.46),  (7.48),  (7.49) и (7.50) 

I"  нукторный электропривод по каналу управления имеет:

эталонную передаточную  функцию четвёртого порядка 

^ « ( р ) =  Ю Т   2 7 т  

2 

/2 

1 

’ 

( 7 5 1 )

ч пленную переходную  характеристику

67

з т  (л/2 + 1 ) ^ - 0 0 8 ( 7 2  + 1 ) ^

т

  _

2 + л/2  С  .  1 

(

----------- 51П— нсоз—  \-е

2 

1 

Т  

Т

-К 2'+1)7

т

  и

-  эталонную амплитудную  частотную характеристику 

1

с е 

/17_12

л

/2^7,80 ?; + 1

64

о,.  ....

(7.52)

(7.53)

68

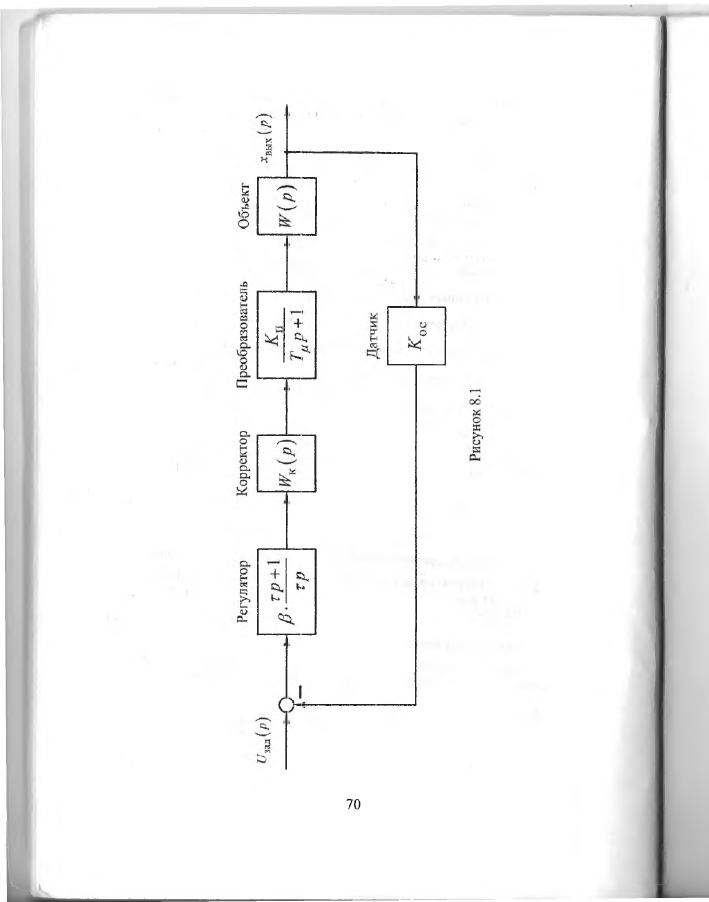
Н а  рисунке  8.1  приведена  структурная  схема  системы  автоматиче­

ского регулирования выходной  координаты инерционного объекта.

Н а рисунке  8.1  имею тся следую щие обозначения: 

где  (7зад 

-   задаю щ ее  напряжение  системы  автоматического  регулиро­

вания  выходной координаты инерционного  объекта;

хвых 

~  выходная координата инерционного объекта;

Р  

-   динамический коэффициент усиления регулятора;

т 

-   постоянная времени регу лятора;

К п 

-   коэффициент усиления преобразователя;

1\х 

-   некомпенсируемая постоянная времени преобразователя;

К ос 

-   коэфф ициент обратной связи;

И'и ( р )  -   передаточная  функция корректора;

Н

р

) 

передаточная  функция инерционного объекта.

Исли  инерционный  объект  первого  порядка,  то  его  передаточная 

функция  имеет вид

№ ( р ) - -

г * - ,  

( 8 - 1 )

Т\р+\

I  Ц|  д 

коэффициент инерционного объекта;

/ 1

постоянная времени инерционного  объекта первого порядка.

11ри  этом корректор долж ен иметь передаточную   функцию:

» ж( р ) ш № ± 1 ,  

(8.2)

цр 

+ 1

I 

постоянная времени корректора.

1

1

и  системы  автоматического  регулирования  вы ходной  координаты 

и 

11

  | 

>11

 н 

11

 м н< >го (>бъекта первого порядка справедливо уравнение 

I , ,  

/  ч 

„  

,   ч-|  п  тр + \  Ц р  + 1 

К п

8 Синтез схемы автоматического регулирования  выходной

координаты  инерционного объекта  первого порядка

70

I

Если выбрать постоянную  времени регулирования.равную  

г  = Тм, 

' 

(8.4)

то  передаточная  функция  системы  автоматического  регулирования  выход­

ной координаты инерционного объекта первого порядка принимает вид

■Л

р

).

1

^ з а д (р )

1

1

_1_

/  ккпк

01 

1

' тмт\Р  + 

1

-■Тмр  + 1

(8.5)

Р  ккпкос

Из сопоставления  эталонной передаточной  ф ункции второго  порядка 

(4.1)  и  передаточной  функции  системы  автоматического  регулирования 

выходной  координаты  инерционного  объекта  первого  порядка  (8.5)  полу­

чаем  систему уравнений:

1

Р  ККПК0с 

1 

1

•V

1

г

2

. 

2  м ’

■Т  = Т

(

8

.

6

)

/ /   К К ПК 0С 

11з системы уравнений (8.6) следует:

// =  

:

ккпкос

'-т„.

(8.7)

1 

ч '/ г

4.

Ган им  образом,  система  автоматического  регулирования  выходной 

•

1

>нишим  инерционного объекта первого порядка имеет: 

на ионную  передаточную  функцию второго порядка

"■<(/>) 

V  

Т Г 7 1 

; 

( 0 )

ос 

р

2

+тмР+\

• иную  переходную характеристику

г  1

МО

1 -

г 

\

. 

I 

I

51П----- НСОЗ —

т 

т

\  

м 

V-]

Г  !

(8.9)

• 

т у ю   амплитудную  частотную  характеристику/

I 

1