Добавлен: 21.10.2018
Просмотров: 1912
Скачиваний: 4
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
11/28
(управление), прикладываемую непосредственно к механической системе. Действие силы U должно
приводить к уменьшению ошибки y.
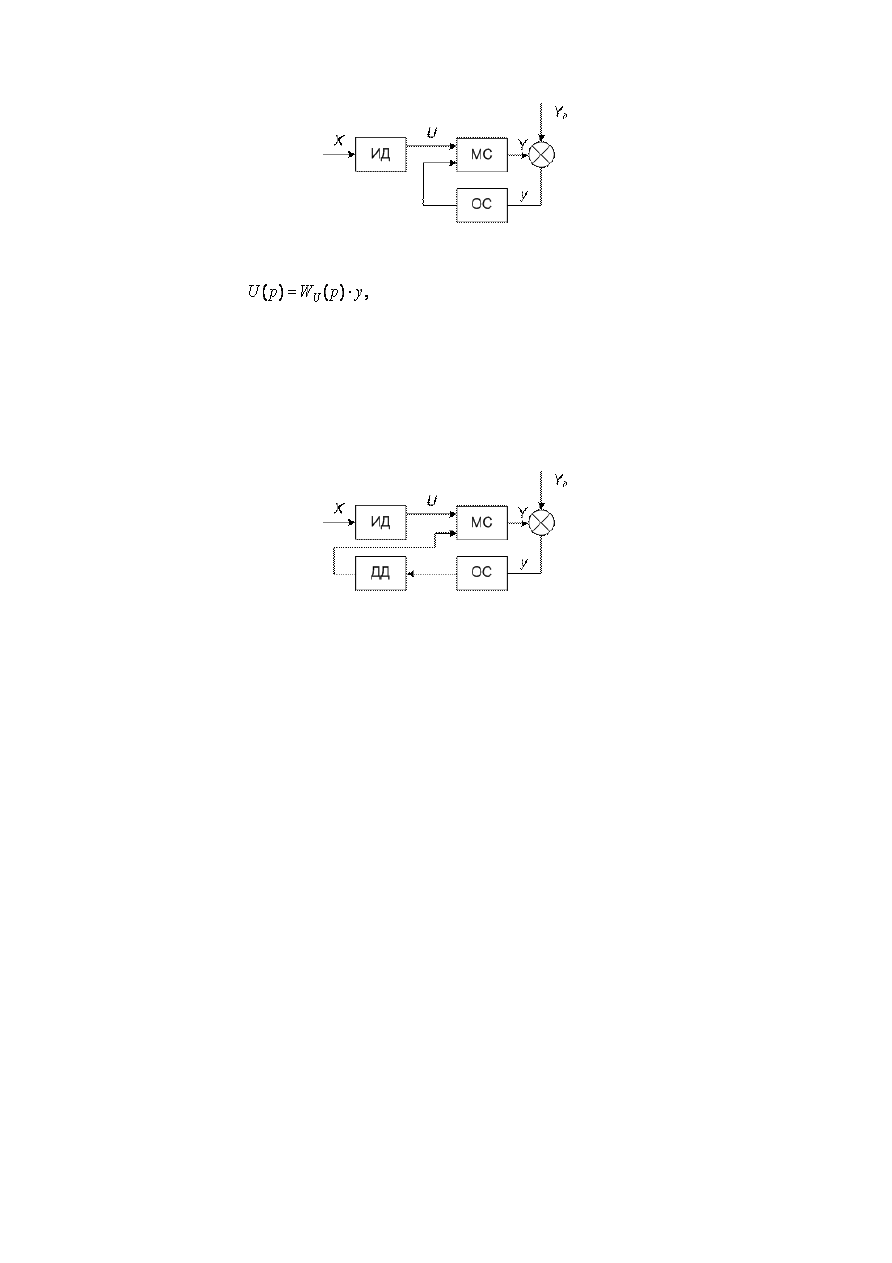
Рис. 11. Функциональная схема системы с силовым управлением
Математически линейная система с силовым управлением описывается выражением вида
(8)
где W
U
(p) – передаточная функция обратной связи.
Системы с силовым управлением подразделяются на пассивные и активные. В пассивных системах для
формирования управления применяют механические элементы: инерционные, упругие или диссипативные.
Простейшими примерами пассивной системы с силовым управлением являются системы с маховиком,
установленным на одном из вращающихся валов машины, динамическим гасителем колебаний или
демпфером. На рис. 12. приведена функциональная схема системы с кинематическим управлением.
Рис. 12. Функциональная схема системы с кинематическим управлением
При кинематическом управлении автоматизированная система МС обладает дополнительной степенью
подвижности. Здесь изменение координаты q* осуществляется дополнительным двигателем ДД по сигналу
ошибки, преобразуемому обратной связью. Сложение дополнительного перемещения с основным
осуществляется дифференциальными механизмами. Такое взаимодействие приводит к компенсации ошибки и
применяется при точном позиционировании механизмов, машин. Для обеспечения малых дополнительных
перемещений МС используют пьезо- или магнитострикционные преобразователи, вибродвигатели, шаговые
двигатели.
В соответствии с приведенными принципами управления находят применение отечественные и
зарубежные разработки электроприводов (ЭП) МС, различающиеся:
·
по роду тока — ЭП постоянного тока с ЭД постоянного тока и ЭП переменного тока с ЭД
переменного тока;
·
по виду УПУ — тиристорный с преобразователем на тиристорах, работающий по схеме
«управляемый выпрямитель-двигатель (УВ-Д)»; транзисторный с преобразовательным устройством в виде
двухтактного усилителя мощности (по схеме ШИП-Д);
·
по типу передаточного устройства — редукторный, безредукторный; электрогидравлический с
гидравлическим передаточным устройством; электромагнитный — с применением фрикционных или
ферропорошковых муфт, выполняющих роль передаточного механизма;
·
по характеру изменения важнейших параметров — нерегулируемый ЭП, параметры которого
изменяются от внешних возмущений, и регулируемый ЭП, параметры которого изменяются и поддерживаются
под действием управляющего устройства;
·
по роду задачи регулирования различают:
а) ЭП со стабилизированным параметром, когда выходная координата поддерживается на заданном
уровне с необходимой точностью;

13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
12/28
б) ЭП программно-управляемый служит для изменения того или иного параметра по заранее заданной
программе;
в) ЭП следящий (СП) отрабатывает изменение выходного параметра в соответствии с произвольно
меняющимся задающим сигналом;
·
по виду управляющего сигнала ЭП разделяют на электроприводы с непрерывным управлением и ЭП
с дискретным управлением. Применение указанных методов управления можно формировать непрерывное
или прерывистое движение выходного вала ИД. По указанному признаку различают ЭП непрерывного и
дискретного действия;
·
по структуре электроприводы подразделяются на разомкнутые, не имеющие ОС, замкнутые и
комбинированные.
3.2. Постановка задачи синтеза системы управления
В настоящее время существует несколько постановок задач проектирования (синтеза)
электромеханических моделей автоматизированных систем, заключающихся в выборе структурной схемы,
параметров, способа технической реализации разработанного модуля из условия выполнения ряда требований
к проектируемой автоматизированной системе и обеспечению ее характеристик. Одним из способов описания
требований к проектируемому ЭММ может служить задание показателей качества работы ЭММ как
допустимое значение статической, динамической и средней квадратической ошибок. При этом должны быть
известны характеристики управляющих и возмущающих воздействий. Детерминированные воздействия
должны быть заданы как функции времени или их производные. Случайные сигналы и помехи должны быть
определены их корреляционными функциями или спектральными плотностями.
Если управляющий сигнал описывается медленно меняющейся функцией времени, а сигнал возмущения
отсутствует, то используют первый способ проектирования САУ ЭММ, выполняя задачу синтеза в следующем
порядке:
1) для объекта управления (ОУ) по техническим условиям выбирают регулирующий орган с силовым
приводом, усилительно-преобразовательное устройство (УПУ) и датчики. Объединяя силовые устройства и
устройства информационного канала линиями связи, формируют неизменяемую часть ЭММ;
2) по статическим и динамическим характеристикам выбранных устройств составляют передаточные
функции отдельных элементов, формируют структурную схему, определяют места включения
корректирующих устройств (последовательное, параллельное и последовательно-параллельное);
3) по заданным требованиям на запас устойчивости по фазе, амплитуде соответственно показателям
качества и точности строят желаемые логарифмические амплитудные (ЛАЧХ
Ж
) и фазовые частотные
характеристики (ЛФЧХ) разомкнутой системы ЭММ;
4) по построенным желаемым (ЛАЧХ
Ж
) и логарифмическим характеристикам неизменяемой
(нескорректированной) части (ЛАЧХ
НС
) определяют коэффициент усиления дополнительно вводимых
промежуточных усилителей, а также тип и параметры корректирующих устройств.
Второй способ используют, когда на синтезируемую систему действует возмущение, описываемое в
форме прямого преобразования Лапласа. В этом случае задачу синтеза выполняют для наиболее полного
подавления возмущения при минимальном значении ошибки в системе.
Третий способ применяют, когда в системе действуют управляющий и возмущающий сигналы
одновременно. В этом случае синтезируемая система должна наиболее точно отрабатывать управляющий
сигнал и подавлять влияние возмущения.
Если характеристики управляющих и возмущающих воздействий известны, то систему управления
можно спроектировать как оптимальную, обеспечив минимальное значение суммарной среднеквадратической
ошибки (при использовании теории оптимальных фильтров Н. Винера и Р. Калмана). Очевидно, что
передаточная функция оптимальной системы зависит не только от характеристик сигнала и помехи, но и от

13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
13/28
выбранного критерия оптимальности (оценки качества работы). При наиболее общей постановке задачи
синтеза оптимальной системы решение находят с учетом достижения минимума функционала (критерия
качества):
(10)
где
— квадратичная форма относительной ошибки системы e(t);
— квадратичная форма относительно сигнала управления U(t); T — время
функционирования системы; a
i
и q
i
— коэффициенты квадратичных форм функционала (10).
Первая квадратичная форма функционала (10) выбирается из требований, предъявляемых к точности
синтезируемой системы, вторая учитывает ограничения на сигнал управления. Задача оптимального синтеза
для рассматриваемого случая может быть сформулирована следующим образом. Из множества U(t) следует
выбрать и технически реализовать такой сигнал управления, который переведет ОУ из начального состояния в
конечное и минимизирует функционал (10). Для решения таких задач применяют различные подходы: методы
вариационного исчисления, принцип максимума Л.С. Понтрягина, метод динамического программирования
Р. Белмана. Однако синтез оптимальных систем из условия минимума функционала (10) достаточно трудно
выполним, поскольку отсутствуют аналитические методы определения связи коэффициентов квадратичных
форм a
i
и q
i
с заданными показателями качества работы синтезируемой системы ЭММ. Значительный перебор
вариантов оптимальных систем с различными видами квадратичных форм и их коэффициентов ведет к
увеличению объема вычислений и росту машинного времени при проектировании электромеханической
системы. Важным фактором также является реализация найденных алгоритмов управления из-за их
сложности и приближенного воспроизведения.
В настоящее время наибольшее распространение при синтезе систем управления электромеханической
системы находит динамический синтез, выполняемый из условия обеспечения допустимых ошибок в
проектируемой системе и удовлетворения других показателей качества работы системы. При проектировании
электромеханической системы всегда нужно стремиться к простоте схемотехнического решения, так как
помимо требования к качеству функционирования в процессе синтеза модуля предъявляются требования и к
его сложности. В качестве функционала сложности проектируемого модуля часто используют следующий
интеграл
,
где W
p
(jω) — частотная характеристика разомкнутой системы; γ — порядок астатизма.
Кроме требований к качеству работы проектируемого электромеханического модуля могут
предъявляться и другие требования: по надежности, стабильности характеристик и массогабаритным
показателям.
3.3. Синтез электромеханического модуля методом амплитудно-частотных характеристик
На этапе статического расчета ЭММ определяется передаточная функция разомкнутой системы:
(11)
где K
p
- коэффициент усиления разомкнутой системы ЭММ; g
= 0, 1, 2,… — порядок астатизма
электропривода, определяемый числом интегрирующих звеньев, и для ЭП астатических первого порядка g
= 1;
g
= 2 — для приводов астатических второго порядка; i — произвольное натуральное число условно
перенумерованных постоянных времени типовых звеньев системы следящего ЭП, располагаемых в (11) в
порядке убывания, т.е. T
1
> T
2
> ... T
i
.
Коэффициент усиления разомкнутой системы следящего электропривода (СЭП):
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
14/28
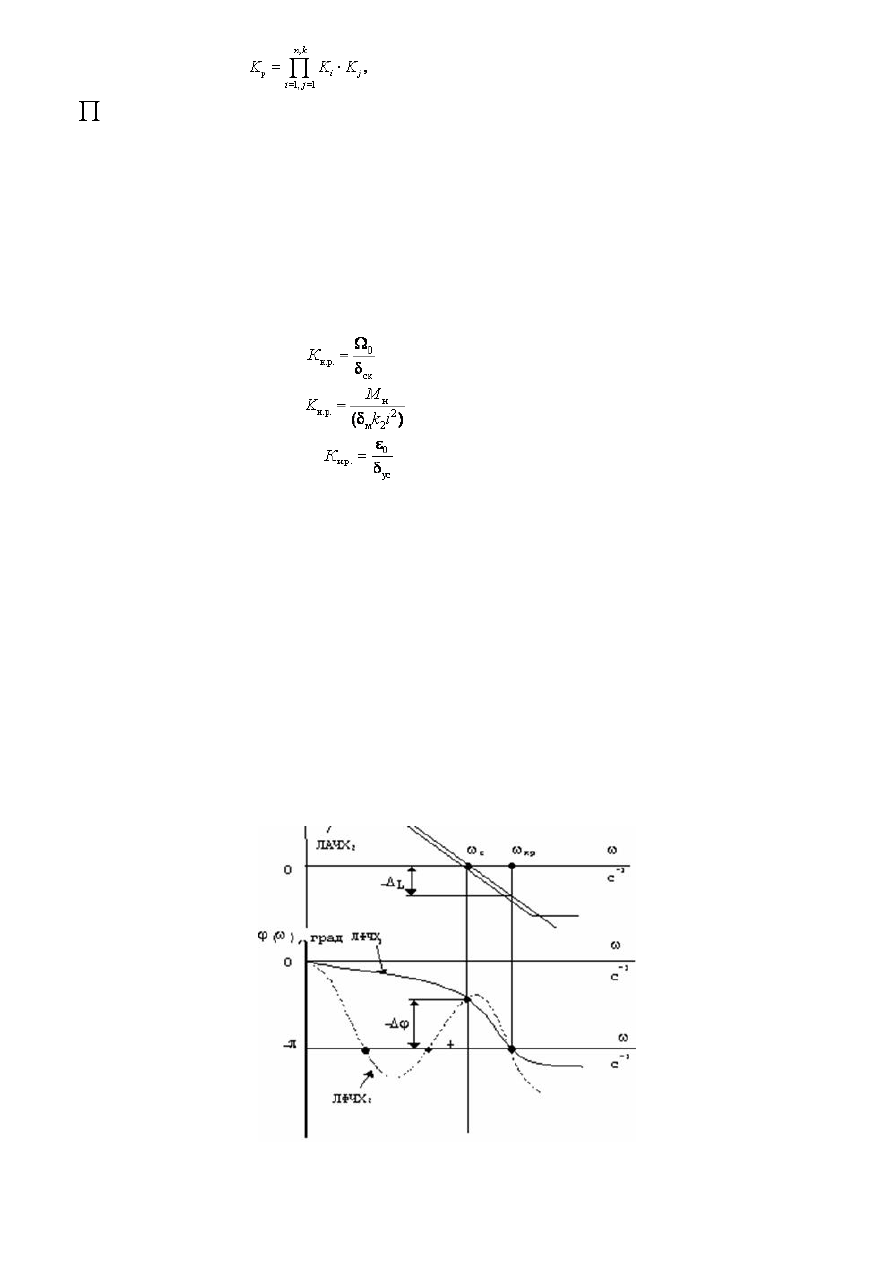
(12)
где
— знак произведения; K
i
, K
j
— коэффициенты передачи звеньев структурной схемы, определяемые
статическими характеристиками элементов АСУ.
Известно, что целью статического расчета системы при синтезе является определение коэффициентов
усиления элементов системы, обеспечивающих требуемую точность поддержания критерия управления. В
зависимости от требований механизмов работа электроприводов может протекать либо преимущественно в
переходных режимах пуска, реверса, торможения, либо в режимах поддержания заданной скорости двигателя.
Выбор вида и параметров ОС для названных режимов производится по-разному. Поэтому для обеспечения
заданной точности СЭП необходимый коэффициент усиления разомкнутого привода (K
н.р.
) рассчитывают по
выражениям при заданных:
·
скоростной погрешности
;
·
моментной погрешности
; (13)
·
погрешности по ускорению
.
где k
2
— коэффициент жесткости (демпфирования) механической характеристики.
В настоящее время для анализа и синтеза электроприводных систем общего применения широко
используют метод логарифмических амплитудно-фазовых частотных характеристик (ЛАФЧХ). К основным
достоинствам метода можно отнести: возможность экспериментального определения ЛАФЧХ реальных
объектов в процессе выполнения исследований СУ и производства наладочных работ СЭП и последующего
синтеза систем управления электроприводами с наперед заданными техническими характеристиками. При
анализе устойчивости нескорректированной системы по ЛАФЧХ разомкнутой системы определяют две
частоты: ω
с
— частоту среза [L(ω)
с
= 0] и частоту ω
п
[g(ω
п
)
= - p].
Для построения ЛАФЧХ исходного ЭП используют выражение (11) передаточной функции разомкнутой
системы с заменой p
= jω, что позволяет получить уравнение для частотной характеристики. Обычно для
определения устойчивости замкнутой системы используют приближенную ЛАЧХ, представляющую собой
асимптотическую ЛАЧХ разомкнутой системы, имеющую точки излома в сопрягающих частотах,
определяемых постоянными временными T
i
звеньев.
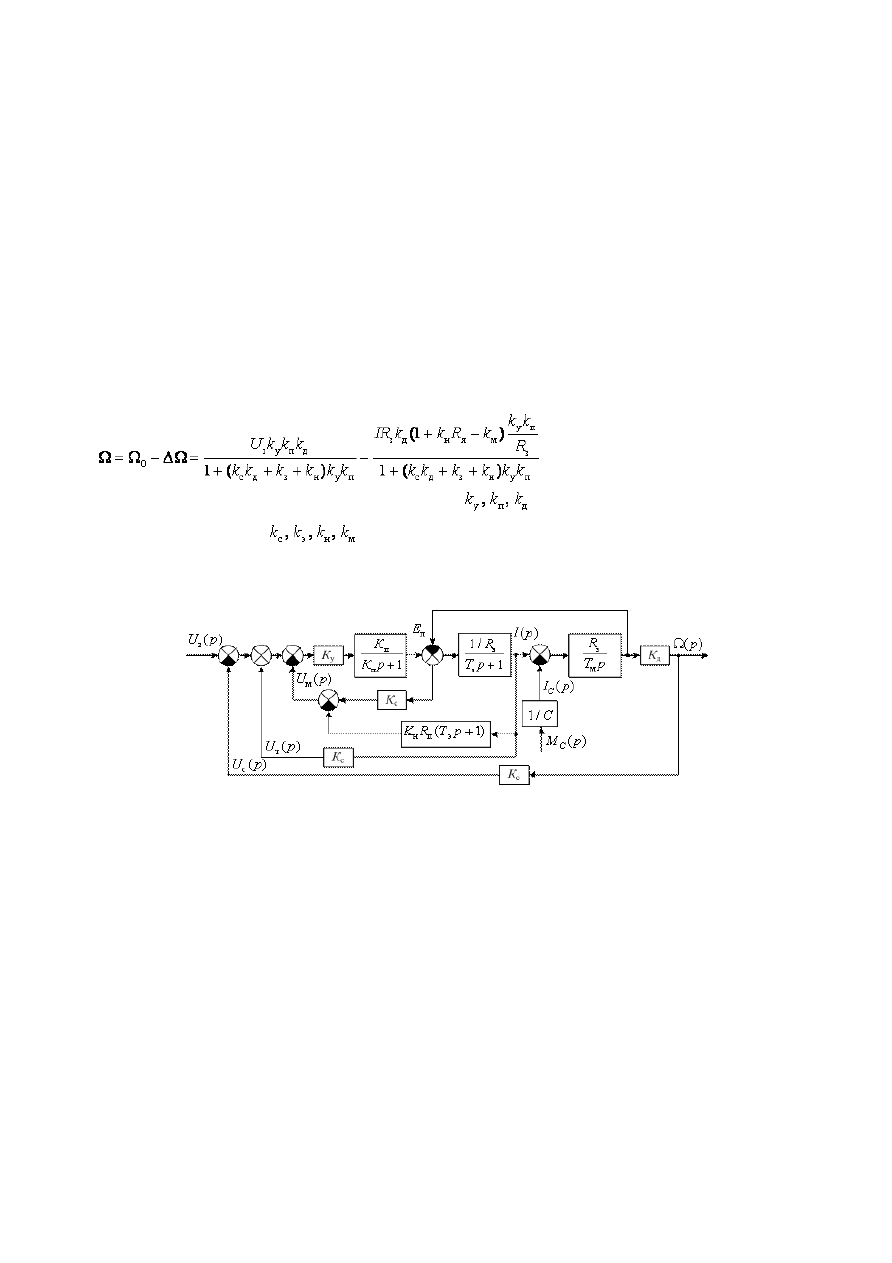
Рис. 13. Оценка устойчивости по ЛЧХ
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
15/28
Точка пересечения ЛАЧХ
1
с осью абсцисс при модуле амплитудно-фазовой характеристики равным
единице определяет частоту среза ω
с
(рис. 13). Другой критической точкой является точка пересечения ЛФЧХ
1
с линией фазового сдвига равного
-p, что соответствует ω
кр
. Известно, что оценку устойчивости САУ(САР)
определяют по запасу устойчивости по амплитуде(
-DL) и запасу устойчивости по фазе (-Dj). Для
удовлетворительного качества регулирования ЭП должны выполняться следующие условия: DL³(10–15) Дб;
Dj³(30–60) град. Если разомкнутая система устойчива (ЛАЧХ
2
), а ЛФЧХ
2
пересекает линию
-p в нескольких
точках, то замкнутая система будет устойчивой, когда L(ω) < 0 при j
= - p, для самой правой из точек
пересечения. Если при анализе окажется, что ω
с
= w
кр
, то рассматриваемая система находится на границе
устойчивости.
3.4. Статический расчет ЭММ
Структурная схема ЭММ с суммирующим усилителем при условном действии всех обратных связей
приведена на рис. 14. Электромеханическая характеристика стабилизации скорости для рассматриваемой
схемы рассчитывается по уравнению, записанному условно при действии всех обратных связей в виде:
(14)
где U
з
– напряжение сигнала задания скорости;
– коэффициенты передачи усилителя,
преобразователя и двигателя;
– коэффициенты передачи датчиков скорости, ЭДС, напряжения и
тока двигателя; R
э
, R
я
– сопротивление цепи «преобразователь – двигатель» и цепи якоря двигателя; Е
п
, Е
д
–
ЭДС преобразователя и двигателя.
Рис. 14. Структурная схема ЭММ с суммирующим усилителем
Из уравнения (14) электромеханической характеристики общего вида можно получить уравнение при
действии конкретной обратной связи, приняв равным нулю коэффициенты других связей.
Выбор обратной связи или комбинации некоторых следует производить на основе следующих
принципов. Обратная связь по скорости является главной связью по регулируемой координате и обеспечивает
наиболее высокую точность стабилизации скорости при наличии тахогенератора. Обратная связь по
напряжению обеспечивает невысокую стабилизацию напряжения питания двигателя, компенсируя падение
напряжения в силовой цепи преобразователя. Поэтому такая обратная связь может использоваться при малых
диапазонах регулирования, определяемых допустимым статизмом электромеханической характеристики.
Положительная ОС по току способна обеспечить высокую точность стабилизации скорости, но
расчетная точность находится в зависимости от нелинейной характеристики управления преобразователя.
Отрицательная ОС по ЭДС применяется при небольших диапазонах регулирования скорости и не
обеспечивает ожидаемую точность регулирования.
Заданная погрешность системы электропривода определяет значение коэффициентов обратных связей,
усилителя и преобразователя. В системе с отрицательной обратной связью по скорости произведение искомых
коэффициентов усиления, передачи можно получить из уравнения: