Добавлен: 21.10.2018
Просмотров: 1913
Скачиваний: 4
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
21/28
Для АСР с объектами, имеющими в своей структуре интегрирующее звено (объекты без
самовыравнивания) необходимо принять Т
3
= 1 и К
0
= 1/Т
0
.
Приложение 1
Варианты заданий
Технологические параметры для курсового проектирования
Объект, параметр
регулирования
Вариант
Возмущение М, %, хода
регули рующего органа
Показатель качества регулирования в абсолютных
значениях
плавное
скачко образное
Δy
уст
Δy
мак
c
tper
,
c
Уровень
Н, м
1
10
10
0,05
0,15
85
2
10
5
0,05
0,15
о<
t
<
3600
3
20
20
0,10
0,25
150
4
20
10
0,10
0,25
80
5
20
15
0,05
0,20
0<
t
<3000
Температура
Θ
, °С
6
10
5
32
1
0<
t
<3200
7
10
10
3
1
0<
t
<3600
8
10
8
2
1
100
9
5
3
1
0,5
30
10
5
5
1
1
50
Скорость
v, м/мин
11
25
10
10
24
150
12
25
5
10
10
90
1
3
10
10
5
10
0<
t
<3000
1
4
10
5
10
10
150
1
5
15
10
10
15
80
Подача (расход)
Q,
л/с
1
6
5
3
0,02
0,05
450
17
5
5
0,02
0,10
300
18
10
10
0,05
0,15
0<
t
<3600
19
10
5
0,05
0,10
250
20
8
5
0,02
0,10
0
<t
<3000
Влажность
m
, %
2
1
10
8
0,5
1,0
150
22
10
5
0,5
0,5
0<
t <
3600
2
3
10
10
0,3
0,5
0
<t
<3000
2
4
20
10
1,0
2,0
200
25
20
5
0,5
1,0
150
Данные экспериментальных кривых разгона технологических объектов управления
Параметр
1
2
3
4
5
6
7
8
9
10
11
12

13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
22/28
H
, м
1,002
1,003
1,012
1,024
1,052
1,096
1,116
1,142
1,18
0
1,192
1,200
1,200
θ
, °
С
80
80,1
80,1
80,2
80,3
80,8
81,1
81,5
83,0
84,0
87,9
90,0
v, м/мин
400
406
422
460
498
548
570
580
597
600
600
600
Q
, л/с
2,00
2,02
2,03
2,07
2,17
2,38
2,52
2,72
3,16
3,42
3,92
4,00
m,
%
10,0
10,1
10,2
10,3
10,8
11,6
12,4
13,1
15,2
16,6
18,2
20,0
t, с
0
20
40
60
100
160
200
250
400
500
1000
3000
Приложение 2
Параметризация моделей второго порядка по переходной характеристике
Основные положения
Весьма распространенным в практике методом испытания объектов управления является скачкообразное
изменение величины на входе (в режиме установившегося сигнала на выходе) и регистрация соответствующей
реакции на выходе. Если пренебречь длительностью скачка и его величину принять за единицу, то изменение
выходной величины по отношению к изменению величины на входе будет представлять переходную
характеристику объекта.
При таком экспериментальном исследовании переходная характеристика часто наблюдается как
апериодический (монотонный) процесс с точкой перегиба или как колебательный монотонно затухающий
процесс и в обоих случаях выходная величина явно стремится к новому постоянному значению. В таких
случаях часто пытаются идентифицировать объект управления как объект 2-го порядка, вычисляя тем или
иным способом коэффициенты дифференциального уравнения (или передаточной функции) по
экспериментальной переходной характеристике.
Первый способ
Рассмотрим два способа вычисления коэффициентов передаточной функции при монотонной
переходной функции с точкой перегиба.
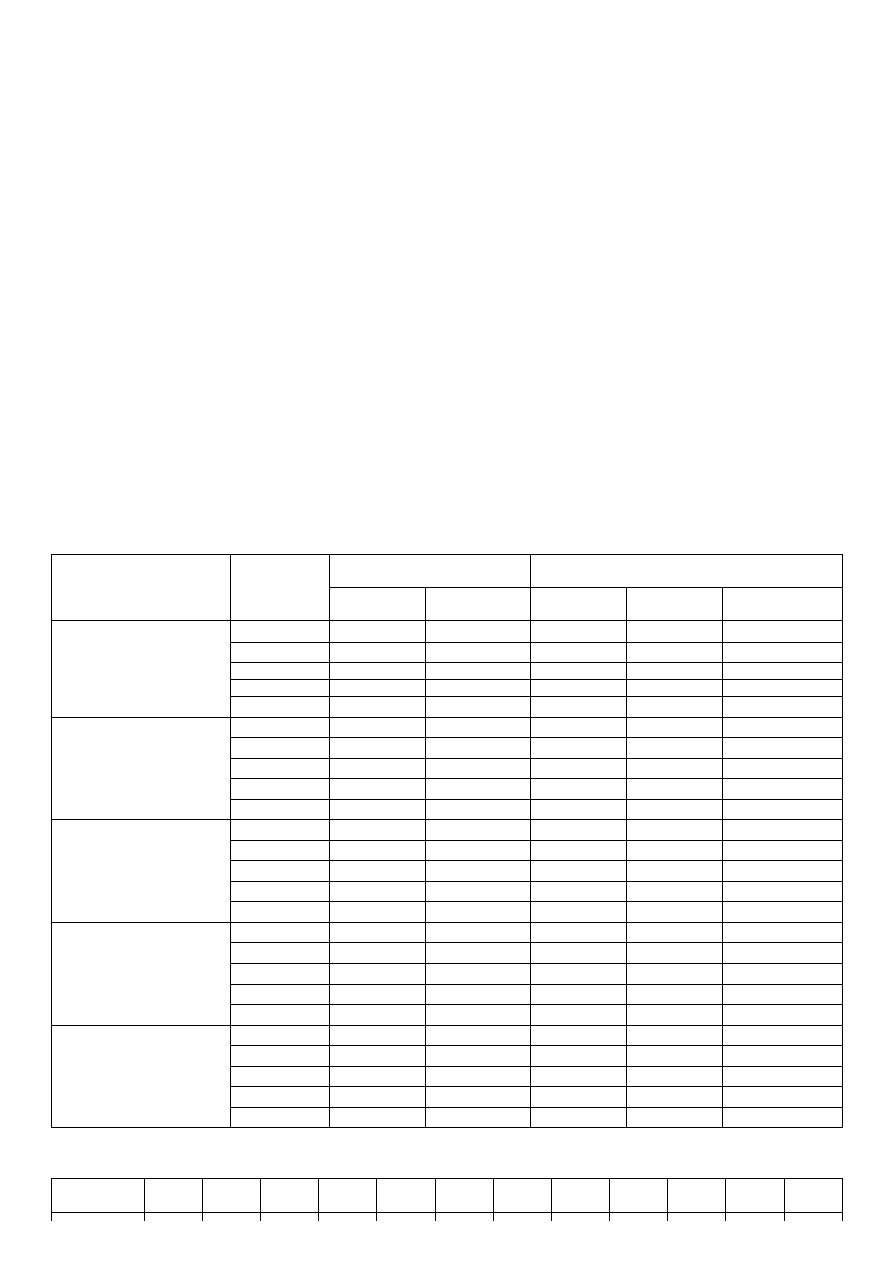
Пусть переходная характеристика имеет вид, представленный на рис. П1.
Оба способа предполагают отыскание точки перегиба на экспериментальной кривой и проведение через
нее касательной до пересечения с горизонтальной осью координат (ось времени) и с асимптотой, к которой
стремится переходная функция.
Первый способ предполагает далее считывание с графика (см. рис. П1) интервалов T
а
и T
b
, второй
способ - T
b
и T
c
.
Передаточная функция ищется в виде
(1)
Будем считать, что статический коэффициент передачи K известен из статической характеристики
объекта. Для определенности положим K
= 1 (см. рис. П1).
Таким образом, по двум интервалам, полученным по экспериментальным данным, необходимо найти две
постоянные времени T
1
и T
2
.
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
23/28
Рис. П1. Измеряемые отрезки на экспериментальной переходной функции
Для объекта с передаточной функцией (1) при K
= 1 переходная функция
, (2)
где d
= T
1
/T
2
и при принятом условии T
1
< T
2
будем иметь 0 < d < 1.
Используя выражение (2), можно получить
(3)
(4)
(5)
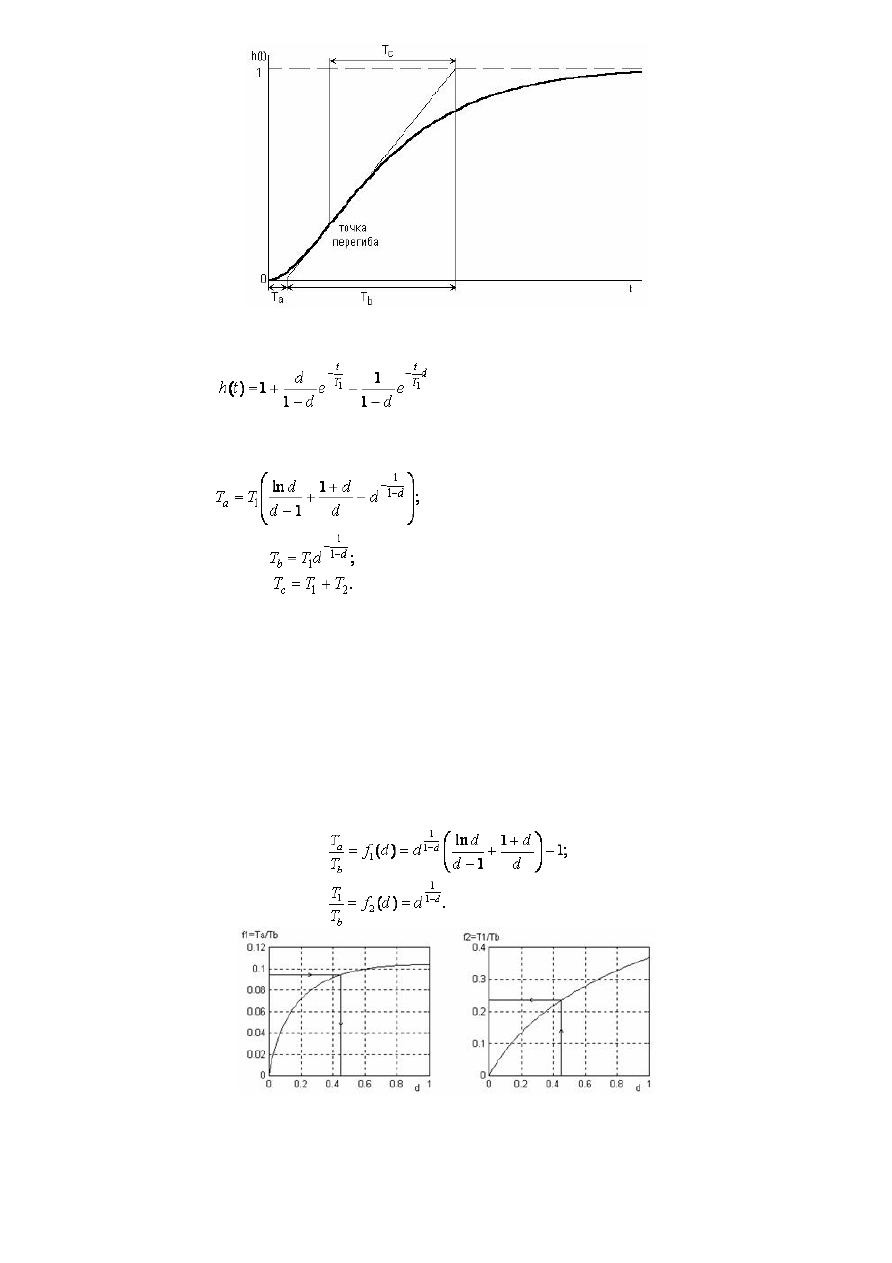
Для быстрой идентификации по первому способу (по T
a
и T
b
) заготавливают обычно два графика на
миллиметровке.
Тогда идентификация сводится к определению по величине отношения T
a
/T
b
величины d с помощью
первого графика. Затем по найденной величине d по второму графику находят отношение T
1
/T
b
, после чего
легко вычисляются T
1
и T
2
(см. рис. П2). Как видно из первого графика на рис. 2 отношение T
a
/T
b
должно
быть меньше некоторого уровня, а именно, необходимо иметь T
a
/T
b
< 3/e
- 1, иначе решение отсутствует и это
может означать, что или отрезки T
a
и T
b
определены слишком грубо или переходная функция не является
переходной функцией звена второго порядка.
Рис. П2. Графики для вычисления постоянных времени по отрезкам T
a
и T
b
При наличии ЭВМ можно использовать m-файл ta_tb.m (см. ниже) в пакете Matlab, который запрашивает
значения Ta и Tb и после решения нелинейного уравнения выдает значения T1 и T2.
clc % ta_tb
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
24/28
% вычисление параметров Т1 и Т2 по отрезкам
% Та и Тb переходной функции звена второго пор.
Ta=input('Отрезок Та = ');
Tb=input('Отрезок Тb = ');
a=Ta/Tb;
if a<3/exp(1)-1
d=.5; dn=1;
while abs(d-dn)>1e-7
dn=d; c=log(d)/(d-1);
d=d+a-exp(-c)*(c+1/d+1)+1;
end
T1=Tb*exp(log(d)/(1-d)); T2=T1/d;
disp('Вычисленные пост. времени')
disp(['T1 = ' num2str(T1)])
disp(['T2 = ' num2str(T2)])
else
disp(['Ta/Tb > 3/e-1 = ' num2str(3/exp(1)-1)])
disp('Решений нет.')
end
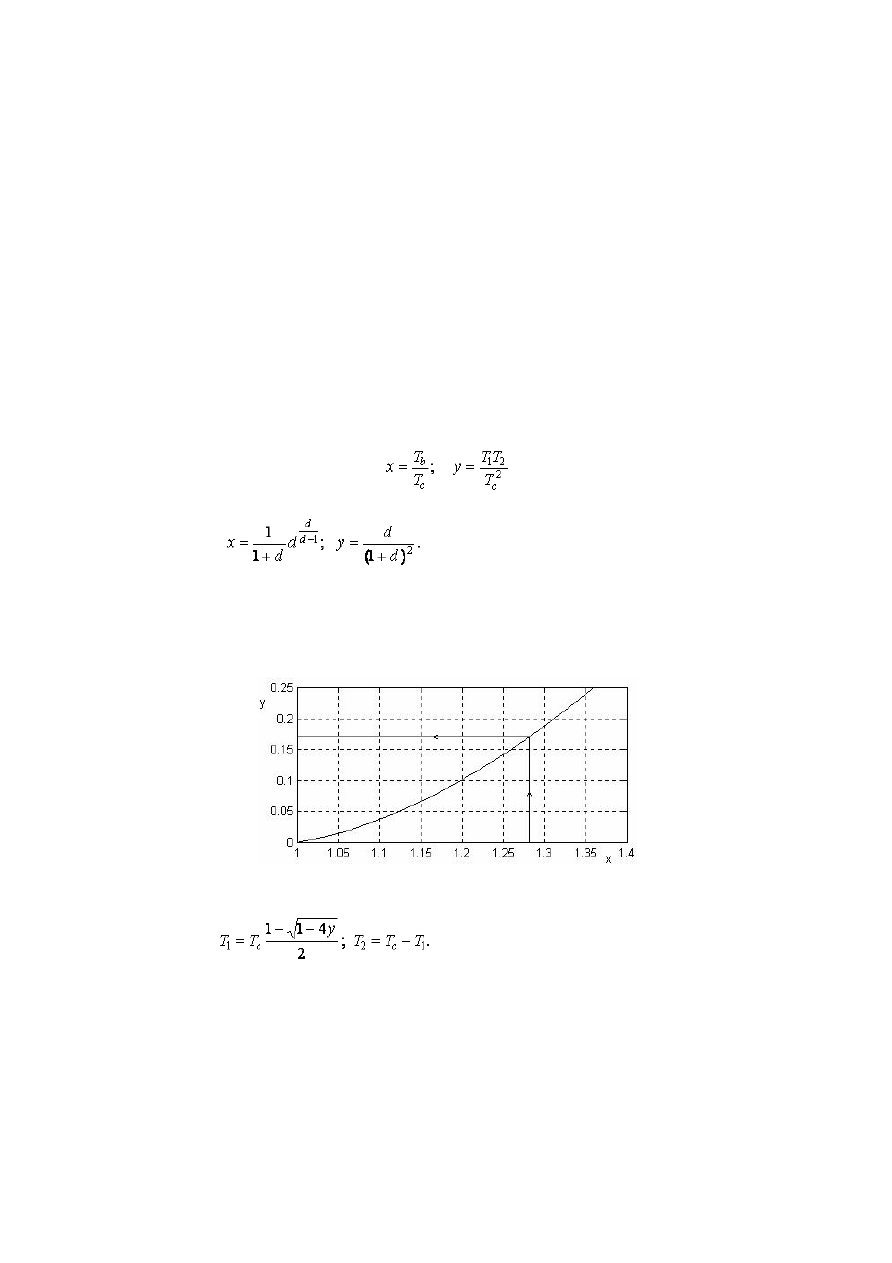
Второй способ
Для идентификации по второму способу (по T
b
и T
с
) вводятся две безразмерные переменные
для которых можно получить из (3), (4) и (5) следующие выражения:
(6)
Обычно, используя уравнения (6) как параметрические уравнения кривой y
= f(x), строят заранее эту
кривую (см. ниже) и пользуются ею для идентификации в следующем порядке. По экспериментальной
переходной характеристике находят T
b
и T
c
(см. рис. П1), вычисляют x
= T
b
/T
c
, по кривой y
= f(x) находят y (см.
рис. П3).
Рис. П3. График для вычисления у по х.
Искомые постоянные времени вычисляются затем по формулам
(7)
На ЭВМ эту же задачу можно решить, например, с помощью простой программы для пакета Matlab:
clc % tb_tc
% вычисление параметров Т1 и Т2 по отрезкам
% Тb и Тc переходной функции звена второго пор.
Tb=input('Отрезок Тb = ');
Tc=input('Отрезок Тc = ');
x=Tb/Tc;
if x>1 & x<exp(1)/2
d1=0; d2=1;
while abs(d1-d2)>1e-7
d=0.5*(d1+d2);
f=x-exp(d*log(d)/(d-1))/(1+d);
if f>0, d1=d; else d2=d; end
13.10.2018
Содержание
https://dec.cdo.vlsu.ru/pluginfile.php/13674/mod_resource/content/0/Yearly_project/KP.htm
25/28
end
T1=Tc*d/(1+d); T2=Tc-T1;
disp('Вычисленные пост. времени')
disp(['T1 = ' num2str(T1)])
disp(['T2 = ' num2str(T2)])
else
disp(['Tb/Tc<1 или Tb/Tc>e/2=' num2str(exp(1)/2)])
disp('Решений нет.')
end
В программе методом половинного деления решается первое из уравнений (6) и по заданному x
находится d. Затем T
1
и T
2
вычисляются по уравнениям (7) с учетом того, что после подстановки y из (6) в (7)
для T
1
получается выражение
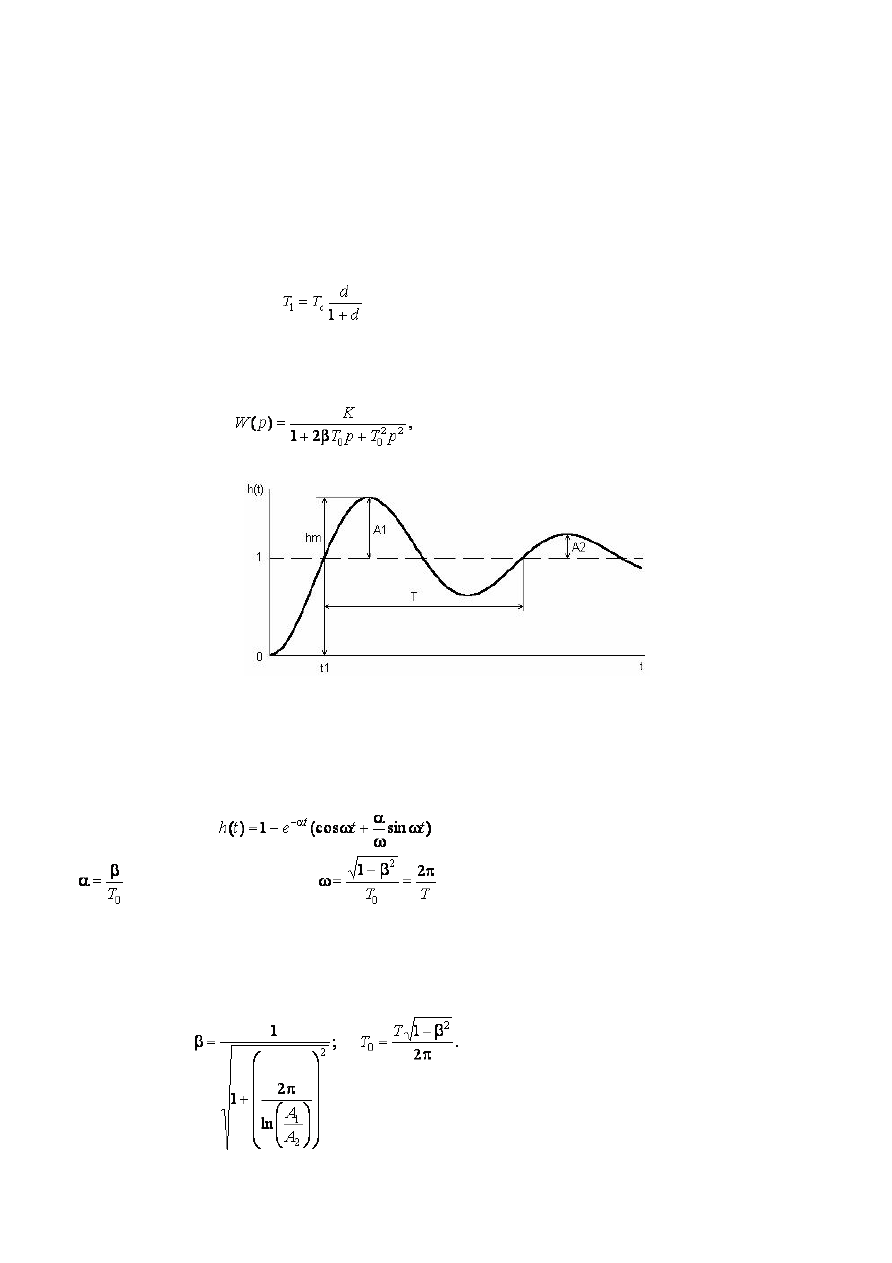
Колебательный характер экспериментальной переходной характеристики
В том случае, когда экспериментальная переходная характеристика обнаруживает колебательный
характер (рис. П4), передаточную функцию ищут в виде
(8)
где β - степень затухания; T
0
- постоянная времени звена.
Рис. П4. Измеряемые отрезки на колебательной переходной функции
Считая по-прежнему, что статический коэффициент передачи K находится из статической
характеристики объекта, положим K
= 1. Тогда из экспериментальной переходной характеристики необходимо
определить степень затухания β и постоянную времени T
0
.
Для объекта с передаточной функцией (8) при K
= 1 переходная функция имеет вид
, (9)
где
- коэффициент затухания,
- круговая частота колебаний.
При малой степени затухания (0
< β < 0,4) экспериментальная переходная функция имеет несколько
максимумов и в этом случае обычно считывают с экспериментальной кривой два последовательных переброса
A
1
и A
2
(рис. 4) и период колебаний T.
Искомые параметры вычисляются по формулам
(10)
Большая степень затухания