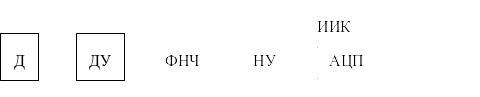Добавлен: 21.10.2018
Просмотров: 900
Скачиваний: 7
Содержание
Цель проекта 4
-
Структура АСНИ 4
-
Описание АСНИ 4
-
Методическое обеспечение 5
-
-
Техническое обеспечение 7
-
Разработка по АСНИ для подсистемы «Спектральный анализ». Среда разработки C++ Builder 8
-
Краткие сведения о среде разработки 8
-
Программирование процессов работы с файлами данных 13
-
-
Проектирование алгоритмов дискретного преобразования Фурье и оценивание спектральной плотности мощности 15
-
Определение дискретного преобразования Фурье 15
-
Определение спектральной плотности мощности 16
-
-
Задание на курсовое проектирование 18
-
Разработка технического обеспечения 18
-
Разработка программного обеспечения 18
-
-
Документация проекта 19
Библиографический список 20
Приложение А 21
Приложение Б 22
Приложение В 23
Цель проекта
Целью курсового проекта является разработка технического и программного обеспечений автоматизированной системы научных исследований (АСНИ).
1. СТРУКТУРА АСНИ
1.1. Описание АСНИ
АСНИ предназначена для спектрального анализа данных, поступающих от первичных преобразователей физических величин, характеризующих некоторый технологический процесс. В состав АСНИ входят следующие подсистемы:
-
подсистема измерений – информационно-измерительный канал (ИИК);
-
подсистема передачи данных;
-
подсистема обработки данных;
-
подсистема визуализации и документирования результатов.
Рисунок 1.1 ‑ Обобщенная структура АСНИ
На рисунке 1.1 приняты следующие обозначения:
ИИК ‑ информационно-измерительный канал;
УСО – устройство связи с объектом;
БД ‑ база данных.
Состав и структура ИИК приведены на рисунке 1.2.
Рисунок 1.2 ‑ Структура информационно-измерительного канала
На рисунке 1.2 приняты следующие обозначения:
Д ‑ датчик;
ДУ – дифференциальный электронный усилитель;
ФНЧ ‑ фильтр нижних частот;
НУ – нормирующий усилитель;
АЦП ‑ аналого-цифровой преобразователь.
ДУ предназначен для усиления сигналов, поступающих от датчиков и подавления синфазных помех.
ФНЧ выполняет функции противомаскировочного фильтра и служит для подавления высокочастотных составляющих сигнала в целях исключения ошибок аналого-цифрового преобразования.
НУ предназначен для согласования входного напряжения АЦП с динамическим диапазоном изменения преобразуемого аналогового сигнала.
1.2. Методическое обеспечение
Одной из важнейших задач, решаемых автоматизированными системами, является сбор и обработка данных, поступающих от первичных преобразователей (датчиков), установленных на объектах автоматизации. Эти данные рассматривают как временные ряды. Временной ряд ‑ это множество наблюдений, генерируемых последовательно во времени. В зависимости от того, как изменяется время: непрерывно или дискретно, различают временные ряды непрерывные и дискретные.
Современные автоматизированные системы обрабатывают данные с помощью компьютеров, поэтому все данные, которые поступают в виде аналоговых сигналов преобразуются в цифровую форму.
При исследовании процесса аналого-цифрового преобразования будут рассматриваться следующие временные ряды:
− исходная
физическая величина (непрерывный ряд);
− выходной
сигнал датчика (в вольтах), соответствующий
функции
(непрерывный временной ряд);
− выходной
сигнал датчика
,
переведенный в непрерывные отсчёты
(фиктивный непрерывный временной ряд);
– выходной
сигнал датчика
,
переведенный в непрерывные отсчёты -
выборки, выполненные в дискретные
моменты времени с периодом Т (дискретный
временной ряд);
− выходной
сигнал датчика
,
переведенный в квантованные отсчёты,
полученные после операции квантования
(дискретный временной ряд);
− ошибка,
равная
−
.
Фиктивный
временной ряд
введен здесь для удобства формализации
описания процесса аналого-цифрового
преобразования и последующего
программирования соответствующего
алгоритма работы АЦП. Как временной ряд
,
так и ряд
измеряются в одних единицах ‑ отсчётах.
При этом элементы ряда
могут принимать как целые, так и дробные
значения, а элементы ряда
принимают только целые значения.
В
роли объектов исследования в данной
работе выступают детерминированные
полигармонические сигналы и сигналы
случайной природы. Структура
полигармонического сигнала
(непрерывного временного ряда) определена
следующим соотношением
, (1.1)
где ak – амплитуда и fk − частота k-ой гармоники; M − количество гармонических составляющих.
Непрерывный
временной ряд
можно представить как результат линейного
преобразования функции
в виде
. (1.2)
Значения дискретного временного ряда С(iT) и соответствующие значения дискретного временного ряда c(i), которые получаются на выходе АЦП, можно связать с помощью следующего соотношения
.
(1.3)
В соотношении (1.3) выражение в квадратных скобках принимает целое значение в результате округления, выполняемого всегда в меньшую сторону.
Добавление к значениям временного ряда C(iT) величины 0,5 обеспечивает повышение точности округления.
Ошибка квантования e(i) определяется следующим соотношением
. (1.4)
Если модель АЦП работает правильно, то значения e(i), будут ограничены интервалом (-0,5; 0,5).
Последнюю формулу (1.4) можно переписать в виде
. (1.5)
В этом случае можно считать, что временной ряд с(i) формируется как сумма соответствующих элементов временного ряда C(iT) и ошибки квантования, которую часто называют шумом квантования.
При идеальном преобразовании ошибка квантования распределена равномерно со стандартным отклонением ~ 0,29 x, где x ‑ шаг квантования.
Основными формулами статической обработки временного ряда ошибки квантования являются
,
,
,
где
‑
математическое ожидание;
‑
дисперсия;
‑ среднеквадратическое отклонение;
‑ разрядность временного ряда.
2. ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
Информационно-измерительный канал системы автоматического управления (рисунок 1.2) состоит из следующих звеньев: датчик, предварительный усилитель, фильтр нижних частот, нормирующий усилитель и АЦП.
Пример расчета информационно-измерительного канала.
Исходные данные для расчета:
-
внутреннее сопротивление датчика R g = 220 Ом;
-
выходное напряжение датчика U g = 2,0 мВ;
-
эффективное значение синфазной помехи, наводимой в витой паре проводов, соединяющих датчик с усилителем, U сф = 1,2 В;
-
максимальная погрешность от синфазной помехи
=3%; -
АЦП работает с частотой f АЦП
=
2000 Гц.
Нужно найти:
-
схемотехническое решение;
-
необходимый КОСС (коэффициент ослабления синфазного сигнала);
-
минимальный коэффициент усиления дифференциального сигнала К ДИФ;
-
величины сопротивлений резисторов;
-
подходящий тип операционного усилителя.
Расчет предварительного усилителя
Так как датчик подключается к ПУ посредством двухпроводной линии, в которой наводится синфазная помеха, то ПУ нужно выполнить по схеме дифференциального усилителя, обеспечивающего необходимое подавление синфазной помехи. Эти схемы более удобны для использования в измерительных системах. Коэффициенты ослабления синфазного сигнала, которые можно получить в этих схемах, в основном зависят от коэффициентов ослабления синфазного сигнала операционных усилителей, а также от Кдиф и Ксинф. На коэффициент усиления синфазного сигнала влияет главным образом точность изготовления употребляемых в схемах резисторов, определяющие действие усилителя. На рис 2.1 приведена схема однокаскадного дифференциального усилителя.
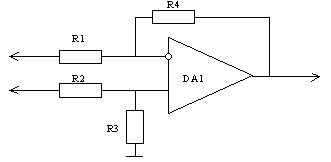
Рисунок 2.1 – Однокаскадный дифференциальный усилитель
Требуемый коэффициент ослабления синфазной помехи вычисляется по фомуле
(86дБ).
Минимально допустимый коэффициент усиления дифференциального сигнала находится в соответствии с методикой [1] по формуле
Кдиф = КОСС∙ Ксинф.
Расчет активного фильтра нижних частот (НЧ)
Считаем, что рабочая полоса ОУ достаточно широкая, поэтому частоту среза находим в соответствии с теоремой Шеннона - Котельникова
.
ФНЧ и УН можно выполнить в виде активного фильтра, собранного на операционном усилителе. В качестве активного фильтра выбираем схему фильтра Саллена-Ки, изображенную на рис 2.2.
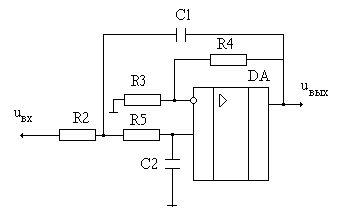
Рисунок 2.2 – Схема активного НЧ фильтра
В соответствии с методикой [2] cначала находится величина емкости конденсатора С1:
=
0,01мкФ.
3. РАЗРАБОТКА ПО АСНИ ПОДСИСТЕМЫ «СПЕКТРАЛЬНЫЙ АНАЛИЗ». СРЕДА РАЗРАБОТКИ MatLab
3.1. Краткие сведения о среде разработки
Программа MATLAB представляет собой высокоуровневый технический вычислительный язык и интерактивную среду для разработки алгоритмов, визуализации и анализа данных, числовых расчетов.
MATLAB сокращенно от Matrix Laboratory, все данные в программе представлены в виде матриц. После запуска MATLAB открываются несколько окон в зависимости от их раскладки и версии MATLAB, основные из них это:
-
Workspace: рабочее пространство. В нем отображаются переменные, с которыми вы работаете в данный момент.
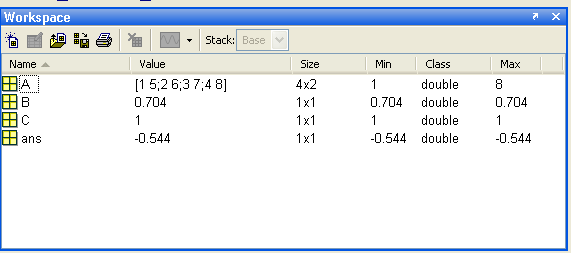
Рисунок 3.1 – Окно рабочего пространства
-
Current Directory: рабочая папка, MATLAB работает с файлами из его папки а также с файлами из рабочей папки, можно добавить свои папки из меню File->Set Path.
Рисунок 3.2 – Окно рабочей папки
-
Command History: история использованных команд. Любую команду можно вызвать еще раз двойным щелчком мыши на ней.
Рисунок 3.3 – Окно истории использования команд
-
Command Window: окно команд, является основным для работы с MATLAB. Команды вводятся после знака “>>”
Рисунок 3.4 – Командное окно
Для примера введем sin(10)
>> sin(10)
Результат:
Рисунок 3.5 – Синтаксис командного окна
ans – сокр. от Answer (ответ) автоматически создаваемая переменная, которая содержит результат вычислений. Переменная ans также появляется в окне Workspace, где можно увидеть ее значение, размерность и т.д. очистить Workspace можно командой clear. Для удаления одной или нескольких переменных надо указать их имена после команды clear (например clear a b c). Для очистки командного окна используется команда clc (не влияет на результаты). Для присвоения переменной определенного значения используется обычный знак равенства “=”. Пример.
Рисунок 3.6 – Командное окно
Можно заметить что переменная ans не создалась поскольку результаты вычислений сохранились в переменных A B C
Для создания вектора строки используется квадратные скобки [] с указанием значений через пробел.
>> A = [1 2 3 4 5]
Результат:
Рисунок 3.7 – Командное окно
Для создания вектора столбца используется квадратные скобки [] с указанием значений через пробел а в конце добавляется
‘>> A = [1 2 3 4 5]'
Результат:
Рисунок 3.8 – Командное окно
Для создания матрицы используется квадратные скобки [] с указанием значений строк через пробел, а разделителем строя является точка с запятой“;”
>> A = [1 2 3 4; 5 6 7 8]
Результат:
Рисунок 3.9 – Командное окно
Для транспонирования матрицы так же в конце надо добавить ‘
>> A = [1 2 3 4;5 6 7 8]'
Результат:
Рисунок 3.10 – Командное окно
Для того чтобы MATLAB не выводил каждый раз значение переменной после ее ввода, надо завершать каждую команду “;”.
Можно писать несколько команд в одной строке разделяя их “;”.
>> A = 5;B = 6;C = 7;
Для создания массива чисел с фиксированным шагом используется двоеточие
>> A = 1:0.1:5;
Результатом будет массив от 1 до 5 с шагом 0,1
Рисунок 3.11 – Окно рабочего пространства
М-Файлы это обычные текстовые файлы с расширением *.m содержащие команды на языке MATLAB. М-Файлы бывают двух типов М-Файлы сценарии и М-Файлы функции. М-Файлы сценарии не имеют входных и выходных параметров. Работают с yпеременными из Workspace.
Также переменные, создаваемые в М-Файлах сценариях после выполнения М-Файла остаются в WorkSpace. Удобны для сохранения часто повторяющихся последовательных команд.
Пример М-Файла сценария “Sample.m”
File->New->M-File
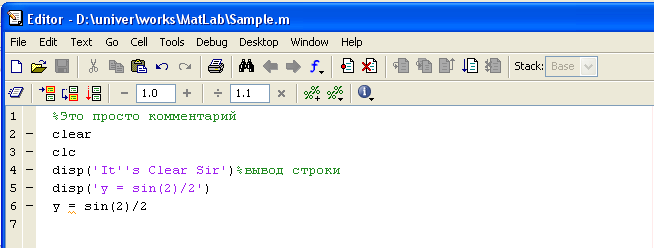
Рисунок 3.12 – Окно М-файла
Код сценария (или скрипта) надо сохранить в папку Current Directory с именем “Sample.m”.
Для выполнения сценария введем команду Sample (MATLAB чувствителен к регистру). Результат:
Рисунок 3.13 – Окно рабочего пространства
Обратите внимание, что в Workspace осталась переменная “y”.
М-Файлы функции имеют входные и выходные параметры. Не могут работать с переменными из Workspace.Переменные создаваемые внутри М-Файла функции уничтожаются после исполнения. Создаются с помощью ключевого слова function.
Необходимо загрузить функцию с файлом в Current Directory.
ВАЖНО: Имя М-Файла функции должно совпадать с именем функции.
Пример М-Файла функции “Sample2.m”
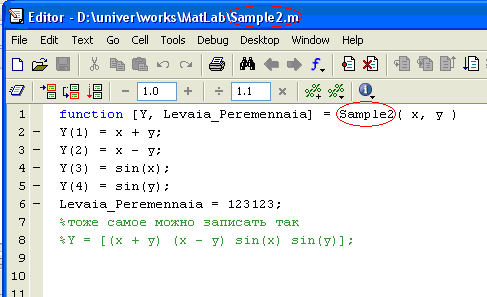
Рисунок 3.14 – Окно М-файла
В строке команд введем
[A B] = Sample2(1, 2)
Результат:
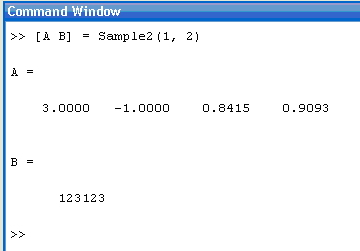
Рисунок 3.15 – Командное окно
Окно Workspace после выполнения функции Sample2
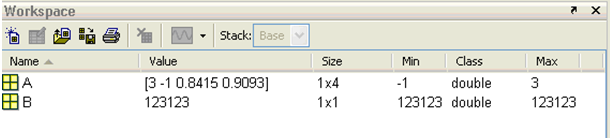
Рисунок 3.16 – Окно рабочего пространства
3.2. Программирование процессов работы с файлами данных
М-файл-функция является типичным объектом языка программирования системы MATLAB. Одновременно он является полноценным модулем с точки зрения структурного программирования, поскольку содержит входные и выходные параметры и использует аппарат локальных переменных. Структура такого модуля с одним выходным параметром выглядит следующим образом: