ПРИЛОЖЕНИЕ А

(рекомендуемое)

Ниже приведен листинг подпрограммы, предназначенной для генерации дискретного временного ряда с неквантованными элементами (без учета влияния АЦП) на языке MАТLAB.

function tsg(szFileName)

%tsg.m - формирует и сохраняет в файле временной ряд данных

%

if nargin == 0

szFileName = 'file.dat'

end

%задаем входные параметры

disp([''ормируем временной ряд:']);

disp(['длина временного ряда ']), n = 2048

disp(['амплитуда ']), a = 1

disp(['вектор частот гармоник ']), fi = [10 40]

disp(['период дискретизации ']), dt = 0.01

% вектор временных отсчетов

t = 0:dt:dt*(n-1);

x = a*sin(2*pi*t*fi(1));

for i=2:length(fi)

x = x+ a*sin(2*pi*t*fi(i));

end

x = x/length(fi);

% открываем файл для записи

fid = fopen(szFileName,'w');

% сохраняем на диске размер временного ряда,

%период дискретизации, амплитуду и временной ряд

fprintf(fid,'%12.8f\n%12.8f\n%12.8f\n%12.8f\n',n,dt,a,x);

% закрываем файл

fclose(fid);

% конец функции

---

ПРИЛОЖЕНИЕ Б

(рекомендуемое)

Ниже приведен листинг программы на языке MatLAB, предназначенной для грубого оценивания СПМ.

%sdpq.m - производит оценивание спектральной плотности

clear; % очищаем рабочую область

% открываем файл для чтения

fid = fopen('file.dat',r);

% заполняем массив значениями из файла

x = fscanf(fid,'%f');

% закрываем файл

fclose(fid);

n = x(1); dt = x(2); a = x(3); x = x(4:length(x));

x = x - sum(x)/length(x); % центрируем временной ряд

t = 0:dt:dt*(n-1);

% формируем вектор отсчетов по частоте

f = (0:(n-1))/(dt*n);

tic; % включаем таймер

% производим преобразование Фурье

y = fft(x);

% выключаем таймер и отображаем полученное значение

disp(['Время прямого преобразования: ' num2str(toc) ' c.']);

% задаем параметры для окна с графиком

set(gcf, 'Name','*Оценка спектральной плотности',...

'Position',[70 100 400 250], …

'MenuBar', 'none',...

'NumberTitle','off',…

'Visible','on');

% задаем параметры для координатной сетки

set(gca, 'Units','normalized',…

'XGrid','on',...

'YGrid','on',…

'NextPlot','add');

%выводим график сплошной зеленой линией

plot(f,abs(y)/dt,'-g');

% производим обратное преобразование Фурье

x = ifft(y);

%выводим график исходного временного ряда

plot(t,x,'-g');

ПРИЛОЖЕНИЕ В

(справочное)

Ниже приведены графики исходного временного ряда и грубая оценка СПМ без сглаживания комплексного спектра, построенные в среде MatLAB.

Исходные данные:

• Количество гармоник – 5;

• Частоты гармоник: 10,20,30,40,50;

• Период дискретизации – 0,001 с;

• Количество элементов - 2048

• Разрядность АЦП – 12

• Амплитуда сигнала – 10 В

• Диапазон входных напряжений от -10 В до +10 В;

• Статическая ошибка – 25%;

• Разрешение по частоте – 5 Гц.

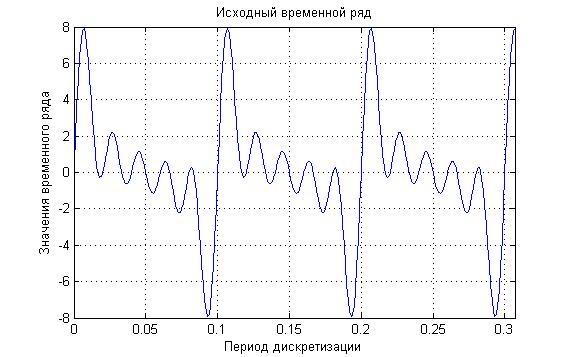
Рисунок 1 – График исходного временного ряда

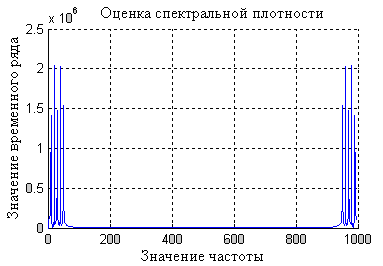
Рисунок 2 – График грубой оценки СПМ

без сглаживания комплексного спектра

---

Смотрите также файлы

• ПРИМЕР_подзадание2 (расчет ряда).doc

• ПРИМЕР_подзадание1 (расчет канала).doc

• контр_ЗАДАНИЕ.doc

• Языки_контр_зао.docx

• ЦЕЛИ_ ЗАДАЧИ_ТЕМЫ КП БД.docx