function var=f_name(Cnncoк_napaмeтpов)

%Основной комментарий

%Дополнительный комментарий

Тело файла с любыми выражениями

vаr=выражение

М-файл-функция имеет следующие свойства: он начинается с объявления function, после которого указывается имя переменной van — выходного параметра, имя самой функции и список ее входных параметров; функция возвращает свое значение и может использоваться в виде name (Список_параметров) в математических выражениях; все переменные, имеющиеся в теле файла-функции, являются локальными, т.е. действуют только в пределах тела функции; файл-функция является самостоятельным программным модулем, который общается с другими модулями через свои входные и выходные параметры; правила вывода комментариев те же, что у файлов-сценариев; файл-функция служит средством расширения системы MATLAB; при обнаружении файла-функции он компилируется и затем исполняется, а созданные машинные коды хранятся в рабочей области системы MATLAB.

Последняя конструкция vаг=выражение вводится, если требуется, чтобы функция возвращала результат вычислений.

Приведенная форма файла-функции характерна для функции с одним выходным параметром.

В пакете MATLAB используютс следующие команды для работы с файлами:

‑ fopen(filename, permission) ‑ открывает файл с именем filename и параметром, определенным в permission и возвращает идентификатор fid со значением: 0 ‑ чтение с клавиатуры (permission установлено в 'r'); 1 ‑ вывод на дисплей (permission установлено в 'а'); 2 ‑ вывод сообщения об ошибке (permission установлен в ' а'); -1 ‑ неудача в открытии файла с выводом сообщения message о типе ошибки. Идентификатор fid часто используется в качестве аргумента другими функциями и программами ввода-вывода. Имя файла filename может содержать путь к файлу. Если открываемый для чтения файл не найден в текущем каталоге, то функция fopen осуществляет поиск файла по пути, указанном в MATLAB;

‑ fids = fopen С all') ‑ возвращает вектор-строку, содержащую идентификаторы всех открытых файлов, не включая стандартные потоки О, 1 и 2. Число элементов вектора равно числу открытых пользователем файлов;

Команда fclose закрывает файл. Она имеет следующие варианты:

‑ status = fclose(fid) ‑ закрывает файл, если он открыт. Возвращает статус файла status, равный 0, если закрытие завершилось успешно, и -1 в противном случае. Аргумент fid ‑ это идентификатор, связанный с открытым файлом (см. функцию fopen для более подробного описания).

‑ status = fclose( 'all') закрывает все открытые файлы. Возвращает 0 в случае успешного завершения и -1 ‑ в противном случае.

4. ПРОЕКТИРОВАНИЕ АЛГОРИТМОВ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ И ОЦЕНИВАНИЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ

4.1. Определение дискретного преобразования Фурье

Дискретное преобразование Фурье (ДПФ) определяется следующим соотношением

, (4.1)

где X(k) ‑ значение (комплексное) дискретного преобразования Фурье, определенное в частоте с номером k; x(i) ‑ значение (вещественное) исходного временного ряда, определенное в момент времени с номером i; T ‑ период дискретизации; N ‑ количество отсчетов (длина) временного ряда.

---

Дискретное преобразование Фурье связывает спектральную характеристику (комплексный спектр) X(k), определенную в дискретных значениях частоты (с номером k), с дискретными значениями временного ряда (сигнала) x(i), определенными в дискретные моменты времени (с номером i).

Масштаб представления спектральной характеристики определяется разрешением по частоте

. (4.2)

По номеру k частоты f_k можно найти ее значение в герцах

(Гц). (4.3)

Аналогично по номеру i времени t_i можно найти его значение в секундах

t_i = iT. (4.4)

Обратное дискретное преобразование Фурье определяется соотношением

. (4.5)

Из сравнения формул (4.1) и (4.5) следует, что они отличаются знаком показателя экспоненты, множителем перед знаком суммы, а также переменной суммирования. Это позволяет строить единые программы для прямого и обратного дискретного преобразования Фурье.

Применяя формулу Эйлера, выражение (4.1) можно привести к виду

, (4.6)

где

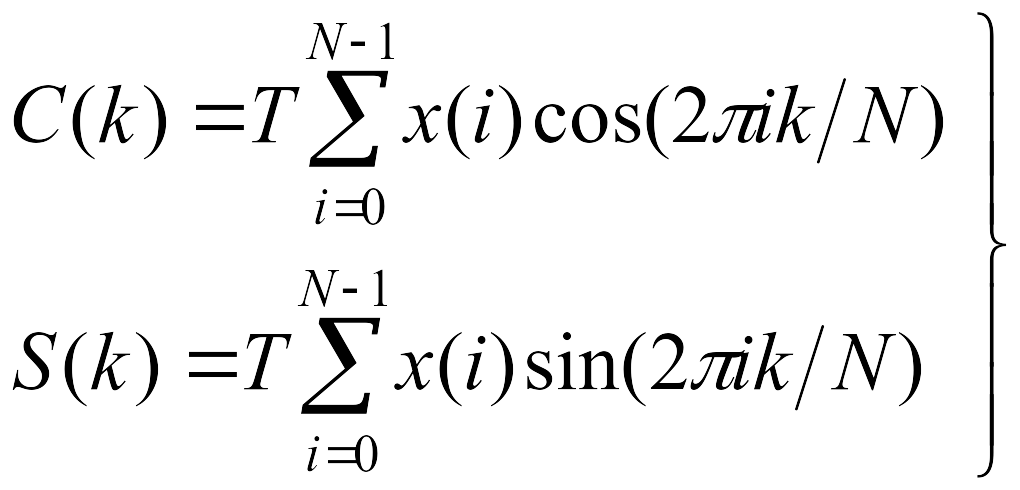. (4.7)

Принимая во внимание (4.7), выражение (4.5) для обратного ДПФ можно привести к виду

,

где

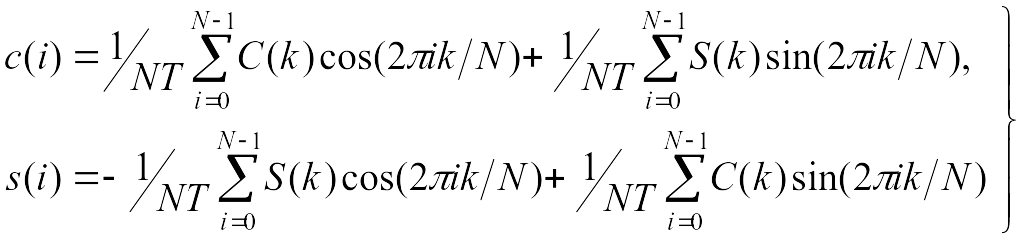, (4.8)

Выражения (4.7) и (4.8) могут быть положены в основу алгоритмов вычисления прямого и обратного ДПФ.

4.2. Определение спектральной плотности мощности

Оценивание спектральной плотности мощности (СПМ) с помощью дискретного преобразования Фурье осуществляется по формуле:

, (4.9)

где X(k) ‑ дискретное преобразование Фурье (спектральная характеристика) временного ряда , соответствующего процессу x(t), обладающего свойством эргодичности.

Черта в правой части формулы (4.9) означает операцию осреднения. Применение формулы (4.9) без операции осреднения приводит к получению "грубой" оценки СПМ. Формула (4.7) позволяет вычислить оценку СПМ посредством статистического осреднения модуля спектральной характеристики совокупности данных, поделенного на длину записи данных.

В спектральном анализе случайных временных рядов на статистическую устойчивость влияют два параметра ‑ разрешение по частоте и длина записи .

Можно показать, что оценки СПМ приближенно имеют распределение с n степенями свободы, где n=2b . Более того, для достаточно больших n, например, , распределение аппроксимируется гауссовским (нормальным) распределением. В этом случае нормированное стандартное отклонение (стандартное отклонение, связанное с оцениваемой величиной, т.е. процентная ошибка, или, в статистической терминологии, "коэффициент разброса") определяется соотношением:

. (4.10)

Величину называют стандартной ошибкой. Если , то . Результат означает, что вычисление оценки СПМ с использованием полной длины временного ряда имеет стандартную ошибку, равную 100 %.

Если отрезок поделить на m участков, то в этом случае:

. (4.11)

Подставляя полученный результат в (3.9), найдем:

. (4.12)

Таким образом, для повышения точности оценивания СПМ необходимо исходный временной ряд длины N разбить на m участков длины Nу, вычислить для каждого i-го участка по формуле (4.9), а затем найти осредненную оценку по формуле:

---

. (4.13)

Число степеней свободы для найденной оценки СПМ можно найти следующим образом:

. (4.14)

Следовательно, для повышения степеней свободы и, соответственно, статистической устойчивости оценок СПМ необходимо увеличивать число участков для осреднения.

Осреднение по частотам:

. (4.15)

Следует отметить, что разрешение по частоте в данном случае определится из соотношения:

. (4.16)

Поскольку операция осреднения линейная, оценку СПМ можно найти, комбинируя осреднение по участкам с осреднением по частотам. При этом сначала выполняется осреднение по участкам, а затем - по частотам. При осреднении по m участкам с последующим осреднением соседних спектральных оценок в итоге получаются оценки, число степеней свободы которых равно . Разрешение в этом случае равно .

Листинг программы определения СПМ приведен в приложении Б.

5. ЗАДАНИЕ НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

5.1. Разработка технического обеспечения

5.1.1. Выполнить расчет информационно-измерительного канала автоматизированной системы научных исследований, состоящего из дифференциального усилителя и активного фильтра по следующим исходным данным:

• внутреннее сопротивление датчика ‑ Rи;

• выходное напряжение датчика ‑ Uc ;

• эффективное значение синфазной помехи, которая наводится в витой паре проводов, соединяющих датчик с усилителем, ‑ Uсф;

• максимальная погрешность от синфазной помехи ‑ .

При этом следует определить:

• необходимый КООС (коэффициент ослабления синфазного сигнала);

• минимально необходимый коэффициент усиления дифференциального сигнала К_диф;

• выбрать схемотехническое решение;

• найти подходящий тип операционного усилителя и рассчитать элементы схемы в соответствии с найденным К_диф.

При расчете активного фильтра учесть, что он подключается к АЦП, который работает с частотой F_д. Порядок фильтра принять равным 2.

5.2. Разработка программного обеспечения

5.2.1. Разработать алгоритм и программу оценивания спектральной плотности с разрешением по частоте не хуже b. При этом рассчитать необходимую длину исходного временного ряда N для периода дискретизации Т и ошибки оценивания .

Язык программирования ‑ С++. Можно воспользоваться готовым программным модулем, содержащим функцию быстрого преобразования Фурье (БПФ).

5.2.2. Разработать интерфейс пользователя в стиле Windows, позволяющий осуществлять управление процессами моделирования временных рядов и их спектрального анализа, включая операции ввода данных, визуализации результатов в виде графиков и таблиц с цифровыми значениями.

Варианты заданий приведены в таблице 1.

Таблица 1 ‑ Варианты заданий на курсовое проектирование

Вариант	Исходные данные
	Rи (Ом)	Uc (мВ)	Uсф (В)	 (%)	Fд (Гц)	b (Гц)	Т (с)	 (%)
0	200	2,0	0,9	3	1000	2	0.005	30
1	100	2,5	1,1	5	500	5	0,002	20
2	300	3,0	1,2	3	2000	5	0,02	25
3	400	2,5	1,0	5	1500	1	0,001	40
4	150	3,0	0,8	3	500	2	0,0025	20

---

Продолжение таблицы 1

5	200	2,0	0,7	3	1000	5	0,001	25
6	300	2,5	1,1	5	2000	5	0,002	30
7	400	3,5	0,9	5	1500	2	0,001	40
8	150	4,0	1,2	3	500	1	0,001	20
9	200	2,0	1,0	5	1000	5	0,002	30

6. ДОКУМЕНТАЦИЯ ПРОЕКТА

6.1. Документация проекта включает техническое задание (ТЗ), пояснительную записку (ПЗ) и графическую часть (ГЧ).

6.2. Пояснительная записка имеет следующую структуру:

• Титульный лист;

• Лист задания;

• Содержание;

• Введение;

• Разработка технического обеспечения;

• Разработка программного обеспечения;

• Руководство пользователя;

• Решение контрольного примера (задача спектрального анализа);

• Заключение;

• Перечень ссылок;

• Приложения.

6.3. Графическая часть должна содержать следующие элементы:

• схему электрическую принципиальную информационно-измерительного канала;

• схему программы.

6.4. В приложениях следует привести листинги разработанных программных модулей.

---

Библиографический список

1. Гарет П. Аналоговые устройства для микропроцессоров и мини-ЭВМ / П. Гарет. – М.: Мир,1981. – 382 с.

2. Гутников В. С. Фильтрация измерительных сигналов / В.С. Гутников. ‑ Л.: Энергоатомиздат,1990. – 192 с.

3. Бобровский С.И. Самоучитель программирования на языке С++ в системе Borland C++ Builder 4.0 / С.И. Бобровский. ‑ М.: ДЕСС, 1999. – 286 с.

4. Гальперин М.В. Практическая схемотехника в промышленной автоматике / М.В. Гальперин. ‑ М.: Энергоатомиздат,1987. – С. 262 ‑ 269.

5. Гутников В.С. Фильтрация измерительных сигналов / В.С. Гутников ‑Л.: Энергоатомиздат,1990. – С. 86 – 97.

6. ГОСТ 2.304-81 «ЕСКД. Шрифты».

7. Отнес Р. Прикладной анализ временных рядов. Основные методы/ Р. Отнес, Л. Эноксон. ‑ М.: Мир, 1982. – 428 с.

8. Шамис В.А. C++ Builder 4.0.Техника визуального программирования / В. А. Шамис. ‑ М.: Нолидж, 2000. – 656 с.

---

Смотрите также файлы

• ПРИМЕР_подзадание2 (расчет ряда).doc

• ПРИМЕР_подзадание1 (расчет канала).doc

• контр_ЗАДАНИЕ.doc

• Языки_контр_зао.docx

• ЦЕЛИ_ ЗАДАЧИ_ТЕМЫ КП БД.docx