ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 8851
Скачиваний: 20
71
Δφ
0
U
p
n
U
Δφ
U
U
p
n
Δφ
0
Δφ
а
б
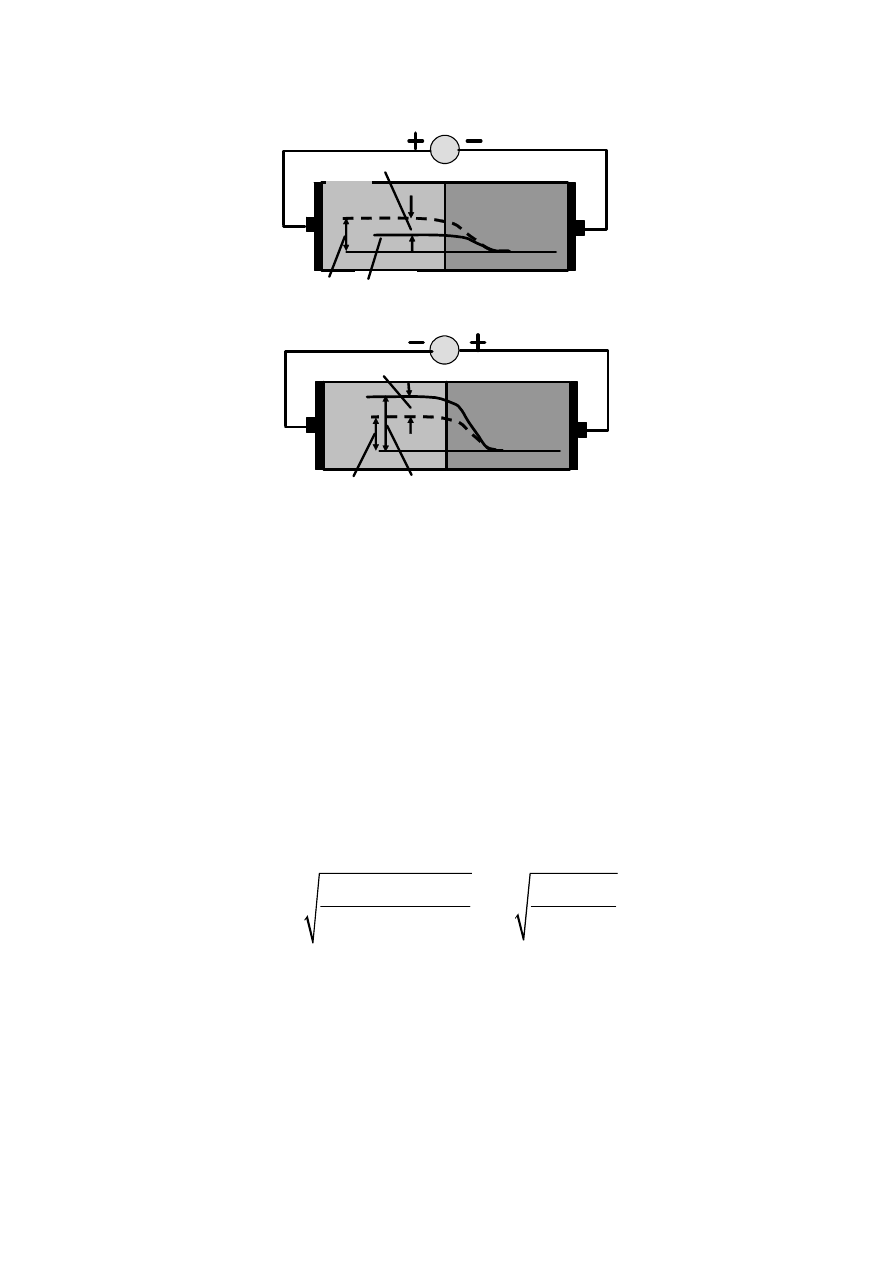
Рис. 2.7 — Смещение перехода в прямом (а)
и обратном (б) направлениях
Такое
включение
перехода
называется
прямым
.
При
отрица
-
тельном
потенциале
на
p -
слое
(
рис
. 2.7,
б
)
высота
барьера
уве
-
личивается
,
и
в
формуле
(2.10)
нужно
изменить
знак
перед
U .
Такое
включение
называется
обратным
.
Изменение
высоты
ба
-
рьера
с
помощью
внешнего
напряжения
приводит
к
изменениям
ширины
перехода
и
граничных
концентраций
носителей
.
Рас
-
смотрим
эти
изменения
применительно
к
несимметричному
пе
-
реходу
с
низкоомным
p -
слоем
.
Подставляя
значение
Δϕ
из
(2.10)
в
(2.96),
получаем
:
0
0
0
0
0
2
(
)
,
Д
U
U
l
l
qN
ξξ Δϕ −
Δϕ −
=
=
Δϕ
(2.11)
где
0
l
—
ширина
потенциального
барьера
при
термодинамиче
-
ском
равновесии
перехода
.
Положительное
приращение
потенци
-
ала
соответствует
уменьшению
потенциальной
энергии
электро
-
нов
,
т
.
е
.
сдвигу
энергетических
уровней
зоны
проводимости
по
-
лупроводника
p
вниз
,
уровней
валентной
зоны
полупроводника
n
вверх
.

72
Как
видим
,
переход
сужается
при
прямом
напряжении
(
U > 0)
и
расширяется
при
обратном
напряжении
(
U < 0).
При
прямом
смещении
вследствие
идеализации
перехода
выражение
(2.11)
имеет
существенную
погрешность
и
отражает
скорее
каче
-
ственную
картину
изменения
ширины
перехода
.
В
то
время
как
при
обратном
напряжении
,
удовлетворяющем
неравенству
T
U
>> ϕ
,
выражение
(2.11)
оказывается
достаточно
точным
и
ши
-
роко
используется
на
практике
.
В
практических
случаях
часто
выполняется
условие
0
U
>> Δϕ .
В
этом
случае
ширину
перехода
можно
записать
в
виде
:
0
0
0
2
.
Д
U
l
U
l
qN
ξξ
=
=
Δϕ
(2.12)
Из
выражения
(2.12)
следует
,
что
изменения
внешнего
напряжения
приводит
к
изменениям
ширины
перехода
,
данное
свойство
широко
используется
на
практике
в
специализирован
-
ных
диодах
—
варикапах
.
Если
в
формулы
(2.4)
подставить
высоту
потенциального
барьера
(2.10)
вместо
равновесного
значения
0
Δϕ
и
считать
кон
-
центрации
основных
носителей
0
n
n
и
0
p
p
неизменными
,
для
гра
-
ничных
концентраций
неосновных
носителей
получим
выраже
-
ния
:
0
0
0
;
T
T
T
U
n
p
p
p
p e
p e
e
−Δϕ
−Δϕ
ϕ
ϕ
ϕ
⎛
⎞
=
= ⎜
⎟
⎜
⎟
⎝
⎠
0
0
0
T
T
T
U
p
n
n
n
n e
n e
e
−Δϕ
−Δϕ
ϕ
ϕ
ϕ
⎛
⎞
=
= ⎜
⎟
⎜
⎟
⎝
⎠
.
Учитывая
,
что
в
скобках
стоят
равновесные
граничные
кон
-
центрации
,
определяемые
формулами
(2.4),
запишем
полученные
выражения
в
следующей
форме
0
;
T
U
n
n
p
p e
ϕ
=
(2.13
а
)
0
.
T
U
p
p
n
n e
ϕ
=
(2.13
б
)
Если
напряжение
U
приложено
в
прямом
направлении
,
то
концентрации
n
p
и
p
n
на
границах
перехода
согласно
(2.13)
73
возрастают
по
сравнению
с
равновесными
значениями
0
n
p
и
0
p
n .
При
3
T
U
= ϕ
концентрации
неосновных
носителей
увеличивают
-
ся
более
чем
в
25
раз
.
Иначе
говоря
,
в
каждом
из
слоев
появляют
-
ся
избыточные
неосновные
носители
,
т
.
е
.
имеет
место
инжекция
(
рис
. 2.8,
а
).
Если
напряжение
U
приложено
в
обратном
направ
-
лении
,
то
граничные
концентрации
n
p
и
p
n
уменьшаются
по
сравнению
с
равновесными
значениями
,
т
.
е
.
имеет
место
экс
-
тракция
(
рис
. 2.8,
б
).
p-полупроводник
n-полупроводник
а
p-полупроводник
Δ
n
p
Δ
p
n
n
n0
n
p0
p
n0
p
p0
l
0
l
x
p,n
10
1
8
10
1
0
p
n-полупроводник
б
Δ
n
p
Δ
p
n
n
n0
n
p0
p
n0
p
p0
l
0
l
x
p,n
10
1
8
10
1
0
n
i
p
n
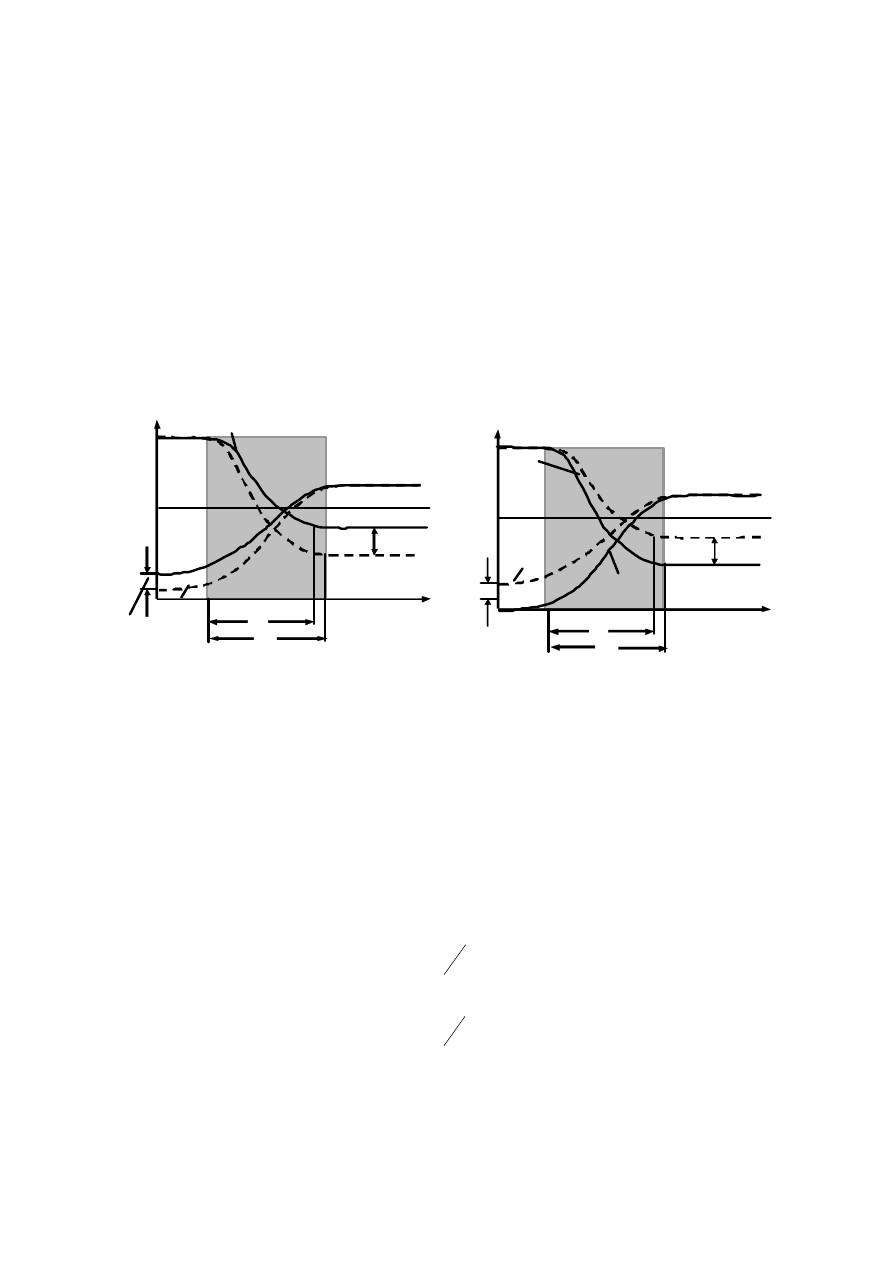
Рис. 2.8 — Распределение носителей в переходе при прямом (а)
и обратном (б) напряжениях. Пунктиром показаны
распределения в равновесном состоянии
Избыточные
концентрации
на
границах
перехода
можно
найти
,
вычитая
из
n
p
и
p
n
соответственно
величины
равновес
-
ных
концентраций
no
p
и
0
p
n .
Выражения
для
величин
избыточ
-
ных
концентраций
можно
записать
в
виде
:
0
1 ;
T
U
n
n
p
p
e
ϕ
⎛
⎞
Δ =
−
⎜
⎟
⎝
⎠
(2.14
а
)
0
1 .
T
U
p
p
n
n
e
ϕ
⎛
⎞
Δ
=
−
⎜
⎟
⎝
⎠
(2.14
б
)

74
Сравним
избыточные
граничные
концентрации
в
слоях
p
и
n ,
разделив
(2.14
а
)
на
(2.14
б
)
и
заменив
в
правой
части
концен
-
трации
0
n
p
и
0
p
n
на
0
p
p
и
0
n
n по
формуле
(1.16).
Тогда
:
0
0
.
p
n
p
n
p
p
n
n
Δ
=
Δ
(2.15)
Для
несимметричных
переходов
концентрации
0
p
p
и
0
n
n
сильно
различаются
,
поэтому
концентрация
инжектированных
неосновных
носителей
будет
гораздо
больше
в
высокоомном
слое
,
чем
в
низкоомном
.
Таким
образом
,
в
несимметричных
пе
-
реходах
можно
считать
,
что
инжекция
носит
односторонний
ха
-
рактер
:
неосновные
носители
инжектируются
в
основном
из
низ
-
коомного
слоя
в
высокоомный
.
Инжектирующий слой с отно-
сительно малым удельным сопротивлением называют эмит-
тером, а слой с относительно большим удельным сопротив-
лением, в который инжектируются неосновные для него но-
сители, — базой.
Формулы
(2.13)
подтверждают
,
что
в
режиме
экстракции
граничные
концентрации
неосновных
носителей
могут
быть
сколь
угодно
малы
,
но
всегда
положительны
.
2.3
Контакты
металл
-
полупроводник
Контакты
полупроводника
с
металлом
играют
важную
роль
в
полупроводниковых
приборах
.
Структура
и
свойства
этих
кон
-
тактов
зависят
в
первую
очередь
от
взаимного
расположения
уровней
Ферми
в
исходных
слоях
.
На
рис
. 2.9
вверху
показаны
зонные
диаграммы
разделенных
слоев
,
а
внизу
—
зонные
диа
-
граммы
соответствующих
контактов
.
Поскольку
уровень
Ферми
в
металле
всегда
расположен
в
зоне
проводимости
и
для
равно
-
весной
системы
должен
быть
единым
,
нетрудно
в
каждом
случае
оценить
характер
результирующей
диаграммы
.
Так
,
на
рис
. 2.9,
а
имеем
Fm
Fp
ϕ > ϕ .
Это
значит
,
что
энергетические
уровни
,
соот
-
ветствующие
зоне
проводимости
полупроводника
,
заполнены
в
металле
больше
,
чем
в
полупроводнике
.
Следовательно
,
после
соприкосновения
слоев
часть
электронов
перейдет
из
металла
в
полупроводник
и
концентрация
электронов
в
металле
в
области
,
75
прилегающей
к
металлургической
границе
,
уменьшится
.
Наличие
дополнительных
электронов
приводит
к
уменьшению
расстояния
между
уровнем
Ферми
и
дном
зоны
проводимости
в
этой
области
,
поэтому
энергетические
уровни
полупроводника
искривляются
вниз
.
Знаки
плюс
и
минус
говорят
о
том
,
что
в
области
металлур
-
гической
границы
образуется
равновесный
поверхностный
по
-
тенциал
so
ϕ
.
На
рис
. 2.9,
б
показан
обратный
случай
,
когда
после
соприкосновения
слоев
электроны
переходят
из
полупроводника
в
металл
и
соответственно
уровни
искривляются
вверх
.
Область
искривления
зон
(
т
.
е
.
область
пространственных
зарядов
)
имеет
протяженность
порядка
дебаевской
длины
.
ϕ
FM
Полупроводник
n-типа
Полупроводник
p-типа
а
б
Запрещенная
зона
ϕ
Fn
ϕ
FM
металл
ϕ
F
ϕ
F
ϕ
Fp
Запрещенная
зона
металл
φ
ЗО
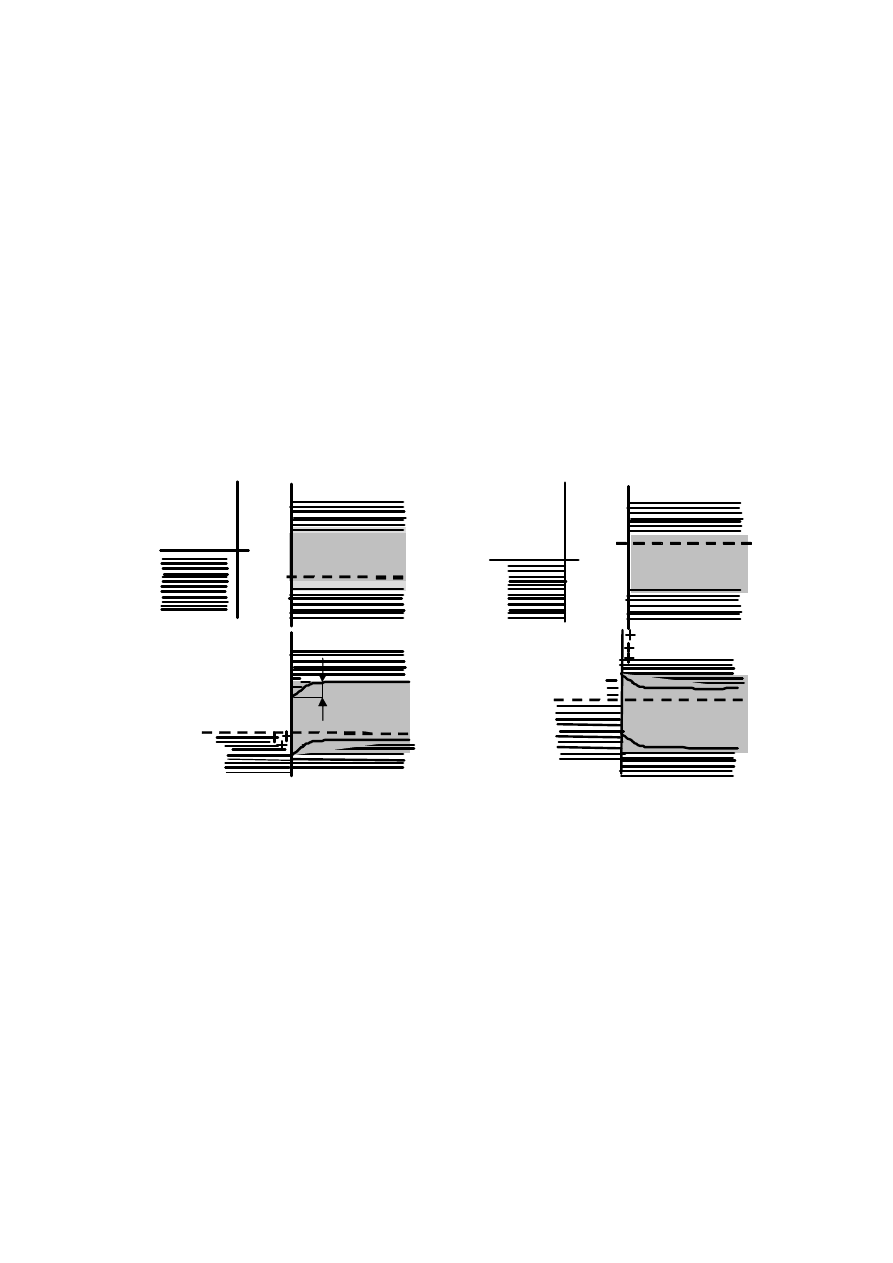
Рис. 2.9 — Зонные диаграммы выпрямляющих контактов
металла с полупроводником: а — контакт с полупроводником
p
-типа; б — контакт с полупроводником
n
-типа
Оба
контакта
,
показанные
на
рис
. 2.9,
а
и
б
,
характерны
тем
,
что
концентрация
основных
носителей
на
границе
полупроводни
-
ка
понижена
по
сравнению
с
концентрацией
вдали
от
контакта
.
Следовательно
,
граничный
слой
обладает
повышенным
удельным
сопротивлением
и
поэтому
определяет
сопротивление
всей
систе
-
мы
.
В
зависимости
от
полярности
приложенного
напряжения
ме
-
няется
высота
приповерхностного
потенциального
барьера
.